Книга: Новый ум короля: О компьютерах, мышлении и законах физики
Похоже ли множество Мандельброта на нерекурсивную математику?
Похоже ли множество Мандельброта на нерекурсивную математику?
Давайте теперь вернемся к нашей предшествующей дискуссии о множестве Мандельброта. Я буду для наглядности предполагать, что это множество является в некотором смысле нерекурсивным. Поскольку его дополнение рекурсивно нумеруемо, то, как следствие, само оно таковым быть не может. Я думаю, что форма множества Мандельброта может кое-чему научить нас о том, что касается природы нерекурсивных множеств и нерекурсивной математики.
Посмотрим еще раз на рис. 3.2, с которым мы встретились в третьей главе («страна Тор'Блед-Нам»). Заметьте, что большая часть множества вписывается в сердцевидную фигуру, которую я обозначил на рис. 4.13 через А (ниже). Эта фигура называется кардиоида и ее внутренняя область может быть определена математически как множество точек с плоскости Аргана, которые удовлетворяют равенству
с = z- z2,
где z — комплексное число, чье расстояние до центра координат меньше 1/2. Это множество является, с очевидностью, рекурсивно нумеруемым в смысле существования алгоритма, который для произвольной точки внутренней области фигуры умеет подтверждать ее принадлежность этой самой области. Этот алгоритм легко получается из указанной выше формулы.
Теперь рассмотрим дисковидную фигуру слева от основной кардиоиды (область В на рис. 4.13).
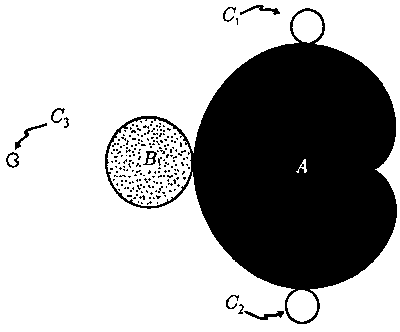
Рис. 4.13. Бо?льшая часть внутренней области множества Мандельброта может быть определена простыми алгоритмическими уравнениями
Ее внутренняя часть представляет собой множество точек
с = z — 1,
где z — удалено от начала координат на расстояние меньше 1/4. Эта область, несомненно, является внутренностью диска, так как представляет собой множество точек, лежащих внутри правильной окружности. И, опять же, эта область является рекурсивно нумеруемой в принятом нами смысле. А как насчет других «бородавок» на кардиоиде? Возьмем две следующие по величине «бородавки». Это практически круглые «кляксы», располагающиеся примерно наверху и внизу кардиоиды на рис. 3.2 и которые на рис. 4.13 обозначены через С1 и С2. Они могут быть описаны как множество
c3 + 2с2 + (1 — z)c + (1 — z)2 = 0,
где z изменяется в пределах круга радиуса 1/8 с центром в начале координат. Фактически, это уравнение дает нам не только обе эти «кляксы», но и «дочернюю» фигуру кардиоидной формы (основную часть рис. 3.1), которая находится слева на рис. 3.2 и которая обозначена как С3 на рис. 4.13. И, аналогично, эти области (как порознь, так и вместе) составляют рекурсивно нумеруемые множества благодаря существованию вышеприведенной формулы.
Несмотря на предположение о нерекурсивности множества Мандельброта, сделанное мной вначале, мы смогли разобраться с его наиболее значительными частями с помощью вполне определенного и достаточно простого алгоритма. Кажется, что такой процесс можно продолжать и дальше. Все наиболее очевидные области множества — и, конечно же, подавляющая часть множества (если не все оно целиком) в процентном выражении — поддаются алгоритмическому анализу. Если, как я предполагаю, все множество все-таки нерекурсивно, то те области, которые недоступны для действия алгоритма, должны быть с необходимостью очень «тонкими» и почти «невидимыми». Более того: когда мы найдем такую область, то вероятнее всего мы смогли бы понять, как нам изменить наш алгоритм, чтобы эта область также оказалась в зоне его действия. Однако, после этого найдутся другие области (если мое предположение о нерекурсивности справедливо), еще более труднодоступные из-за тонкости и сложности своей структуры, перед которыми будет бессилен даже наш усовершенствованный алгоритм. И вновь «волшебство» интуиции, искусства и техники, наверное, позволит нам вычленить эту область; но другие в очередной раз ускользнут от нас; и так будет повторяться снова и снова.
Я полагаю, что этот путь не слишком отличается от того, который часто используется в математике для решения трудных и, предположительно, нерекурсивных задач. Многие задачи, с которыми сталкиваются в некоторых специфических областях, часто решаются с помощью простых алгоритмических процедур — процедур, известных, быть может, на протяжении веков. Но некоторые из этих задач могут не поддаться таким методам, и тогда приходится искать более сложные пути к их решению. Такие задачи будут, конечно, сильнее всего интриговать математиков и подталкивать их к развитию все более мощных методов, в основу которых будет закладываться все более и более глубокое интуитивное понимание природы используемых математических объектов. Возможно, в этом есть что-то от того, как мы познаем окружающий нас физический мир.
В задачах покрытия и задачах со словами, рассмотренных выше, можно уже уловить, как применяется подобный подход (хотя это не те области математики, где аппарат развит в достаточной степени). Мы смогли привести очень простое доказательство для того, чтобы показать невозможность трансформации одного слова в другое при помощи установленных правил. Нетрудно вообразить, что более «продвинутые» методы доказательства способны помочь в более сложных случаях. Не исключена вероятность, что эти новые подходы могут быть превращены в алгоритмические процедуры. Мы знаем, что ни одна процедура не может удовлетворять всем примерам задачи со словами, но те из них, которые ускользают из «алгоритмических сетей», должны быть очень тонко и аккуратно сконструированы. Конечно, как только мы узнаем принцип построения таких примеров — как только мы будем уверены, что в неком конкретном случае произошла «осечка» алгоритма, — мы сможем усовершенствовать наш алгоритм так, чтобы он включал и этот частный пример. Ускользать могут только пары «неравных» слов, так что, как только мы находим такую «ускользающую» пару, мы можем быть уверены в их «неравенстве» и присовокупить этот критерий к нашему алгоритму. Так наше более глубокое понимание ведет ко все более совершенным алгоритмам!
- Программа Гильберта для математики
- Формальные математические системы
- Теорема Геделя
- Математическая интуиция
- Платонизм или интуиционизм?
- Теоремы геделевского типа как следствие результатов, полученных Тьюрингом
- Рекурсивно нумеруемые множества
- Является ли множество Мандельброта рекурсивным?
- Некоторые примеры нерекурсивной математики
- Похоже ли множество Мандельброта на нерекурсивную математику?
- Теория сложности
- Сложность и вычислимость в физических объектах
- 5. Заглянем в вычислительную математику
- Множество большого-тета
- Множество потоков, соревнующихся между собой за обладание единственным ресурсом
- Множество О
- Множество форм одной программы
- 3. Корреляция. Почему множество каузальных утверждений ошибочны
- 8. «Это было похоже на тотальную войну»
- У11.11 Модуль "множество"
- 5.25 Множество адресов для одного интерфейса
- .NET Compact Framework как подмножество платформы для настольных компьютеров
- Листинг 15.9. Неэффективная организация диалога с Web-службой, в которой используется множество вызовов
- Обучающее множество




