Книга: Новый ум короля: О компьютерах, мышлении и законах физики
Является ли множество Мандельброта рекурсивным?
Является ли множество Мандельброта рекурсивным?
Существенной характеристикой нерекурсивных множеств является их сложноорганизованность. Это свойство должно, в некотором смысле, препятствовать любым попыткам систематизации, которая, в противном случае, привела бы к некоторой «работающей» алгоритмической процедуре. Для нерекурсивного множества не существует общего алгоритмического пути к решению вопроса о принадлежности ему произвольного элемента (или «точки»), В начале третьей главы мы встретились с неким чрезвычайно сложно выглядящим множеством — с множеством Мандельброта. Хотя правила, по которым оно строится, поразительно просты, само множество представляет собой бесконечное разнообразие в высшей степени замысловатых структур. Может ли это быть примером настоящего нерекурсивного множества, явленного глазам смертных?
Читателю, однако, не понадобится много времени, чтобы сообразить, что эта парадигма сложности была создана специально для наших глаз волшебством вычислительных технологий с использованием современных быстродействующих компьютеров. А не являются ли компьютеры истинным воплощением алгоритмических действий? Конечно, это так, но все же мы должны принимать во внимание способ, с помощью которого компьютеры, в действительности, создают эти картинки. Чтобы проверить, принадлежит точка плоскости Аргана — комплексное число с — множеству Мандельброта (закрашено черным) или его дополнению (светлая область), компьютер, начиная с нуля, применит отображение
z ? z2 + с
сначала к z = 0, чтобы получить с; потом к z = с, чтобы получить с2 + с; затем к z = с2 + с, чтобы получить с4 + 2с3 + с2 + с; и так далее. Если эта последовательность 0, с, с2 + с, с4 + 2с3 + с2 + с… остается ограниченной, то соответствующая точка с будет черной; в противном случае — белой. Как машина определяет, что такая последовательность остается ограниченной? В принципе, этот вопрос предполагает наличие информации о том, что происходит после бесконечного числа ее элементов! Сама по себе эта задача вычислительными методами не решается. К счастью, существуют способы предсказать исходя уже из конечного числа членов, когда последовательность станет неограниченной. (На самом деле, если последовательность достигает окружности радиуса 1 + ?2 с центром в начале координат, можно с уверенностью сказать, что она будет неограниченной.)
Таким образом, дополнение к множеству Мандельброта является, в некотором смысле, рекурсивно нумеруемым. Если комплексное число с расположено в светлой области, то существует алгоритм, подтверждающий этот факт. А как насчет самого множества Мандельброта — темного участка рисунка? Существует ли алгоритм, способный точно установить, что точка, принадлежащая предположительно темному участку, действительно ему принадлежит? Ответ на этот вопрос в настоящее время, похоже, отсутствует[85]. Я справлялся у многих коллег и экспертов, но ни один из них не слышал о подобном алгоритме. Равно как и никто из них не сталкивался с указанием на то, что такого алгоритма не существует. По крайней мере, насколько можно об этом судить, алгоритм для темной области на сегодняшний день неизвестен. Возможно, множество, дополнительное по отношению к множеству Мандельброта, действительно является примером рекурсивно нумеруемого, но не рекурсивного множества!
Прежде чем исследовать дальше это предположение, необходимо будет обсудить некоторые моменты, которые я ранее опускал. Эти вопросы будут довольно важны для нас в дальнейших рассуждениях по поводу вычислимости в физике. Я хотел бы заметить, что, на самом деле, я был несколько неточен в предшествующем изложении. Я применял такие понятия, как «рекурсивно нумеруемый» и «рекурсивный», к множествам точек в плоскости Аргана, т. е. множествам комплексных чисел. Но эти термины могут применяться только лишь для натуральных чисел и других счетных множеств. Мы видели в третьей главе («Сколько же всего действительных чисел»), что действительные числа не могут быть счетным множеством, равно как, следовательно, и комплексные — ведь любое действительное число может быть рассмотрено как частный случай некоторого комплексного числа с нулевой мнимой частью (гл.3 «Комплексные числа»). В действительности существует такое же «количество» комплексных чисел, как и действительных, а именно «С». (Чтобы установить взаимнооднозначное соответствие между комплексными и действительными числами, можно, грубо говоря, просто взять действительную и мнимую части комплексного числа (записанные в десятичной форме) и перемешать через одну поразрядно цифры из мнимой части с цифрами из вещественной, образуя, тем самым, действительное число: тогда, например, 3,6781…+ i512,975… будет соответствовать действительному числу 50 132,6977851…)
Дабы избежать этой проблемы, можно было бы ограничиться только вычислимыми комплексными числами, так как мы еще в третьей главе видели, что вычислимые действительные числа — а значит, и соответствующие им комплексные — являются счетными. Однако здесь кроется одна принципиальная трудность: не существует алгоритма, с помощью которого можно было бы сравнивать два вычислимых числа, полученных алгоритмически! (Мы можем алгоритмическим образом составить их разность, но мы не в состоянии будем выяснить, равна она нулю или нет. Представьте себе два алгоритма, которые генерируют цифры 0,99999… и 1,00000…, соответственно; мы никогда не узнаем, продолжаются ли нули и девятки в них до бесконечности — так, что числа оказываются равными — или же где-то в дробной части того или другого числа могут появиться иные цифры, делая эти числа неравными.) Таким образом, мы, возможно, никогда не сможем определить, равны ли между собой такие числа. Как следствие этого — наша неспособность решить даже в таком простом случае как единичный круг в плоскости Аргана (множество точек, лежащих на расстоянии не большем единицы от начала координат — черная фигура на рис. 4.4), лежит ли комплексное число в этом круге или нет.
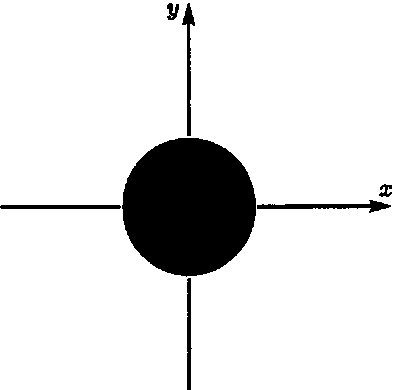
Рис. 4.4. Единичный круг, безусловно, должен рассматриваться как рекурсивное множество, но это требует определенных соглашений
Трудность возникает не с точками, лежащими внутри или снаружи, а именно с точками на самой границе круга — то есть на самой единичной окружности. Эта окружность рассматривается по условию как часть круга. Предположим, что нам уже предоставлен в распоряжение алгоритм для получения цифр вещественной и мнимой частей некоторого комплексного числа. Если мы предполагаем, что это комплексное число лежит на единичной окружности, то мы не можем с необходимостью подтвердить этот факт. Не существует алгоритма, чтобы установить, является ли вычислимое число x2 + y2 равным единице, что служит критерием для принадлежности комплексного числа х + iy данной единичной окружности.
Очевидно, это совсем не то, что нам нужно. Единичный круг, безусловно, должен рассматриваться как рекурсивное множество. Едва ли найдется сколь-нибудь значительное число множеств, более простых, чем единичный круг! Чтобы обойти эту проблему, одним из способов может быть игнорирование границы. Ведь для точек, лежащих внутри (или снаружи), безусловно существует алгоритм, устанавливающий этот факт. (Можно просто последовательно генерировать цифры числа х2+у2, и, в конце концов, мы найдем цифру, отличную от 9 в дробной части 0,9999… или отличную от 0 — в дробной части 1,00000…) В этом смысле единичный круг является рекурсивным. Но этот подход чрезвычайно неудобен для математики, поскольку там часто возникает необходимость ссылаться в рассуждениях на то, что происходит именно на границах. С другой стороны, вполне возможно, что такая точка зрения окажется применимой в области физики. Позднее нам еще придется вернуться к этому вопросу.
Существует другой метод, имеющий непосредственное отношение к данному вопросу, который не предполагает вообще обращения к вычислимым комплексным числам. Вместо того, чтобы пытаться пронумеровать комплексные числа внутри или снаружи рассматриваемого множества, мы просто будем вызывать алгоритм, который для любого наперед заданного комплексного числа будет определять, принадлежит оно нашему множеству или же его дополнению. Говоря «наперед заданный», я подразумеваю, что для каждого числа, которое мы рассматриваем, нам некоторым — быть может, «волшебным» — образом известны цифры мнимой и вещественной части, одна за другой, и в таком количестве, сколько нам нужно. Я не требую, чтобы существовал алгоритм, известный или неизвестный, для нахождения этих цифр. Множество комплексных чисел считалось бы «рекурсивно нумеруемым», если бы существовал хотя бы единственный алгоритм такой, что для любой заданной ему вышеуказанным образом последовательности цифр он бы говорил «да» после конечного числа шагов тогда и только тогда, когда комплексное число действительно принадлежит этому множеству. Оказывается, что как и в случае подхода, предложенного выше, эта точка зрение также «игнорирует» границы. Следовательно, внутренняя и внешняя области единичного диска будут каждая по отдельности считаться рекурсивно нумеруемыми в указанном смысле, тогда как сама граница — нет.
Для меня совершенно не очевидно, что какой-либо из этих методов дает то, что нам нужно[86]. Философия «игнорирования границ», будучи приложенной к множеству Мандельброта, может привести к потере большого числа тонких моментов. Одна часть этого множества состоит из «клякс» — внутренних областей, а другая — из «усиков». Наибольшие сложности при этом связаны, видимо, с «усиками», которые могут «извиваться» самым причудливым образом. Однако, «усики» не принадлежат внутренней части множества, и, тем самым, они были бы проигнорированы, используй мы любой из двух вышеприведенных подходов. Но даже при таком допущении остается неясность, можно ли считать множество Мандельброта рекурсивным в том случае, когда рассматриваются только «кляксы». Похоже, что вопрос этот связан с некоторым недоказанным предположением, касающимся самого множества, а именно: является ли оно, что называется, «локально связным»? Я не собираюсь здесь разбирать значение этого понятия или его важность для данного вопроса. Я хочу просто показать, что существует ряд трудностей, которые вызывают неразрешенные на сегодняшний день вопросы, касающиеся множества Мандельброта, чье решение — первоочередная задача для некоторых современных математических исследований.
Существуют также и другие подходы, которые могут использоваться с тем, чтобы обойти проблему несчетности комплексных чисел. Вместо того, чтобы рассматривать все вычислимые комплексные числа, можно ограничиться только подмножеством таких чисел, для любой пары которых можно вычислительным путем установить их равенство. Простым примером такого подмножества могут служить «рациональные» комплексные числа, у которых как мнимая, так и вещественная части могут быть представлены рациональными числами. Я не думаю, однако, что это дало бы многое в случае «усиков» множества Мандельброта, поскольку такая точка зрения накладывает очень значительные ограничения. Более удовлетворительным могло бы оказаться рассмотрение алгебраических чисел — тех комплексных чисел, которые являются алгебраическими решениями уравнений с целыми коэффициентами. Например, все решения z уравнения
129z7 — ЗЗz5 + 725z4 + 16z3 — 2z — 3 = 0
— это алгебраические числа. Такие числа будут счетными и вычислимыми, и задача проверки двух из них на равенство будет решатся путем прямого вычисления. (Как выясняется, многие из них будут лежать на границе единичного круга и «усиков» множества Мандельброта.) И мы можем по желанию рассматривать вопрос о рекурсивности множества Мандельброта в терминах этих чисел.
Возможно, что алгебраические числа оказались бы подходящим инструментом для двух обсуждаемых нами множеств, но они не снимают все наши трудности в общем случае. Пусть мы рассматриваем множество (темная область на рис. 4.5), определяемое неравенством
y ? ez,
где х + iy(= z) — точка в плоскости Аргана.
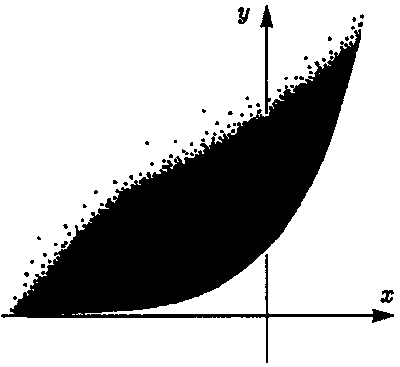
Рис. 4.5. Множество, определенное экспоненциальным соотношением у ? еz, должно также рассматриваться как рекурсивное
Внутренняя часть множества, равно как и внутренняя часть его дополнения, будут рекурсивно нумеруемыми в соответствии с любой из вышеизложенных точек зрения, но (как следует из знаменитой теоремы Ф.Линдеманна, доказанной в 1882 году) граница, у = ех, содержит только одну алгебраическую точку, а именно точку z = i. В этом случае алгебраические числа никак не могут нам помочь при исследовании алгоритмической по своей природе границы!
Несложно определить другой подкласс вычислимых чисел, которые будут подходить в данном конкретном случае, но при этом все равно останется ощущение, что правильный подход нами до сих пор так и не был найден.
- Программа Гильберта для математики
- Формальные математические системы
- Теорема Геделя
- Математическая интуиция
- Платонизм или интуиционизм?
- Теоремы геделевского типа как следствие результатов, полученных Тьюрингом
- Рекурсивно нумеруемые множества
- Является ли множество Мандельброта рекурсивным?
- Некоторые примеры нерекурсивной математики
- Похоже ли множество Мандельброта на нерекурсивную математику?
- Теория сложности
- Сложность и вычислимость в физических объектах
- Что делать, если при установке принтера появляется сообщение Невозможно завершение операции. Подсистема печати недоступн...
- При копировании с жесткого диска на «флэшку» иногда появляется сообщение о дополнительной присоединенной информации, кот...
- Является ли выбранный партнер наилучшим для вас?
- Если не работать за компьютером десять минут, на экране появляется одна и та же заставка. Как ее сменить?
- При входе в систему появляется сообщение о невозможности найти какой-то файл. Как его убрать?
- Подключаю «флэшку», она определяется Windows, но диск в Проводнике не появляется
- Вот уже в который раз при работе в сети появляется сообщение от других пользователей. Что это может быть?
- При загрузке Windows появляется сообщение – неправильный файл boot. ini. За что этот файл отвечает и как исправить данну...
- Появляется «синий экран» с ошибкой, что делать?
- При установке драйвера появляется сообщение об отсутствии у драйвера цифровой подписи
- При печати появляется сообщение об ошибке подсистемы Диспетчера очереди печати. Что делать?
- Появляется сообщение об ошибке Недостаточно виртуальной памяти, файл подкачки отсутствует или слишком мал. Что делать?




