Книга: Почему

Измерение причинности

Измерение причинности

Один из подходов к причинному осмыслению – попытка найти модель, удовлетворяющую данным или объясняющую их. Но сделать это вычислительными методами крайне сложно, и в ряде случаев мы просто хотим узнать о взаимосвязях в некоем наборе уже измеренных переменных. То есть, возможно, нам нужно всего лишь выяснить причины рабочей производительности, а не выстроить полную модель, включающую все измеренные переменные. Рандомизированные испытания занимаются именно этими вопросами (каково действие конкретного лекарства на уровень смертности?), однако эксперименты можно проводить не во всех случаях, и им свойственны собственные ограничения (см. главу 7).

Еще один вид причинно-следственных рассуждений связан с квантификацией силы индивидуальных каузальных зависимостей. Если отпуск – причина производительности, а не наоборот, то сила отпуска как причины производительности должна быть выше, а обратной посылки – ниже. Эти корреляции симметричны, но мера каузальной значимости должна учитывать асимметрию таких отношений. Кроме того, она должна в некотором смысле быть пропорциональна информативности причины относительно следствия, а также ее полезности как цели вмешательства для получения следствия. Если отпуск случайно спровоцировал производительность, при этом многочасовая работа всегда ее повышает, тогда отработанные часы имеют больше каузальной силы, чем дни отдыха. Аналогично если принуждать людей брать отпуск – эффективная стратегия повышения производительности, а заставлять работать по многу часов – нет, перерыв в работе окажется более значимой причиной производительности.

Если, однако, отпуск ведет к производительности только потому, что снижает текучку персонала, а более опытные сотрудники демонстрируют более высокую производительность труда, желательно убедиться, что весомость опыта для производительности выше, чем значимость отпуска. То есть требуется найти самые непосредственные причины (на рассмотренных нами графах это родительские переменные, а не отдаленные потомки).

Но, если мы в силах оценить причины производительности совершенно независимо от причин любой другой переменной, можно выполнить меньше тестов, причем реально проводить их параллельно друг другу (что повышает эффективность компьютерных программ для расчета этих переменных). Также это означает, что вместо применения аппроксимации[253] (например, исследования подгруппы графов, а не всех возможных), когда многократный прогон программы каждый раз дает разные результаты, расчеты будут достаточно просты, чтобы использовать точные методы.

С другой стороны, есть ограничение: без структуры, показывающей связи между всеми переменными, нельзя брать полученные результаты непосредственно для прогнозирования. Скажем, мы обнаруживаем, что партийная поддержка – это причина, по которой сенаторы голосуют за законопроекты, и поддержка избирателей тоже может быть причиной. Но это ничего не говорит о взаимодействии между этими двумя видами поддержки, а также о том, будет ли результат сильнее, чем просто сумма двух причин. Одно из решений – найти более сложные взаимосвязи. Вместо того чтобы использовать любые измеренные переменные, можно выстроить конъюнкцию («законопроект поддерживают и партии, и избиратели»), выяснить, как долго некий фактор должен быть истинным (день, месяц, год и т. д.), и найти последовательности событий (будут ли результаты одинаковыми, если начать прием первого лекарства перед вторым?).

Не вдаваясь в детали, скажем, что существуют методы как для представления, так и для тестирования такого рода сложных взаимосвязей[254].

Одна из возможных мер каузальной значимости – условная вероятность следствия при условии причины. Проще говоря, мы можем посмотреть, насколько отпуск повышает вероятность высокой производительности труда. Однако, как мы увидели в предыдущей главе, многие непричины также усиливают возможность других событий. Если отработанные часы и отпуск имеют общую причину, то они, по всей видимости, умножают вероятность друг друга.

Есть масса мер силы причинно-следственных связей[255], однако главное – каким-то образом включить сюда другую информацию и учесть общие причины. Так, допустим, мы знаем, что и отпуск, и сверхурочные увеличивают производительность труда, но, если присутствуют только сверхурочные, одно только знание об отпуске производительность не повысит.

На практике, однако, можно не измерять переменную напрямую. Возможно, мы не можем узнать точно, сколько часов люди работают, но мы в курсе, сколько времени они проводят в офисе. Некоторые из сотрудников на рабочем месте могут затягивать обеденный перерыв или тратить время на личную переписку и видеоигры. Используя только показатель офисных часов, не получится провести различие между этой категорией и теми, кто находится на месте меньше, но работает продуктивнее. С учетом этого обстоятельства такой индикатор рабочих часов не будет идеально экранировать следствия.

Подобный пример сродни тем, в которых мы изучали репрезентативность переменных (комбинации факторов против каждого отдельного) и ее влияние на результаты выводов о причинности. Итак, нам может понадобиться не только набор переменных для верного отделения причин от следствий. Также следует ожидать, что по этой и другим причинам (упущенные данные, ошибки измерений и т. д.) может иметь место некая вероятностная связь между переменными в отсутствие причинной зависимости, и придется выяснять, как с ними работать.

Если мы говорим, что отпуск – причина производительности, то имеем в виду, что факт отпуска важен для производительности. Если это действительно сильная причина, а требование эффективности не предъявляется ни к какому другому фактору (скажем, достаточный уровень дохода, чтобы отпуск не повлиял на финансы), то, независимо от значения других переменных (например, количества отработанных часов), производительность после отпуска должна повышаться.

И это не будет истинным для всех ситуаций, поскольку многие причины могут иметь как положительные, так и отрицательные следствия: к примеру, ремни безопасности в целом предотвращают летальные исходы дорожных происшествий, но иногда вызывают их, не давая выбраться из затонувшего автомобиля. Мы, однако, по-прежнему можем допустить, что даже если ремни безопасности иногда становятся причиной смерти, в среднем те, кто ими пользуется, имеют более низкие шансы погибнуть в автокатастрофе, чем остальные.

Чтобы квантифицировать (то есть выразить в численном виде) важность причин, можно в среднем вычислить, какое значение имеет причина с точки зрения вероятности ее следствий. Фактически идея заключается в том, чтобы выяснить, насколько изменяется вероятность следствия при отсутствии или наличии причины, если все остальное постоянно. Обстоятельства можно взвесить по критерию их вероятности; если причина значительно повышает вероятность следствия в часто повторяющемся сценарии, это значит больше, чем повышение вероятности в редких случаях.

Возьмем каузальную структуру на рис. 6.8, где партийная поддержка и идеология влияют на голосование политиков, но не предпочтения их избирателей. Если это истинный набор взаимоотношений, тогда в зависимости от того, поддерживают избиратели законопроект или нет, вероятность голосования «за» будет в точности такой же, хотя будут наблюдаться изменения при смене идеологии и партийных предпочтений.

Рис. 6.8. Средняя значимость избирателей для голосования будет стремиться к нулю. Обратите внимание, что графы без обведенных кружками узлов не представляют байесовские сети

Один из методов расчета причинной значимости – сразу зафиксировать значения всех переменных[256] и взглянуть на различия в следствии для каждого заданного значения. Партия может выступать за или против законопроекта, идеологические предпочтения могут совпадать с ним или нет, равно как и избиратели. Итак, мы можем взять каждую комбинацию и посмотреть, какое значение оказывает одобрение электората для любого соединения партийной поддержки и идеологических переменных. Поскольку эти две переменные полностью определяют исход голосований, разницы не будет никакой.

Однако при добавлении переменных каждый из возможных сценариев будет отмечен не слишком часто, и мы, возможно, не увидим достаточно примеров, чтобы вывести статистически значимые заключения. Более практичная мера значимости, чем разработанная мной, предусматривает наличие одновременно только одной константы, при этом для усреднения различий причина либо вводится, либо нет[257]. Для расчета этой меры причинной значимости ?_avg мы выясним, какое значение оказывают избиратели, взяв константой партийную поддержку законопроекта, а потом сделаем то же самое для идеологии и так далее, в итоге сведя все отличия воедино, чтобы получить средний показатель для значимости избирателей.

По большей части в методах, основанных на вероятностях (например, как этот), берется набор данных и высчитывается число, обозначающее причинную значимость одной переменной по сравнению с другой. Это значение может находиться в диапазоне от – 1 до 1, где –1 – сильная отрицательная причина, мешающая следствию произойти, а 1 – сильная положительная причина следствия.

Поскольку обязательно будут помехи, ошибки и упущенные данные, нельзя сделать допущение, что нечто, не оказывающееся причиной, всегда будет иметь нулевое значение. Вместо этого, как правило, необходимо определить, какие значения меры причинной значимости будут статистически значимыми (вспомним разговор о p-значениях и тестирование множественных гипотез в главе 3)[258].

К примеру, когда мы рассчитываем среднюю причинную значимость большого количества потенциальных причин, при этом нет истинных причинных взаимосвязей, распределение рейтингов значимости (значений ?_avg) будет выглядеть как колоколообразная (гауссова) кривая, или как светло-серые столбцы на рис. 6.9. Если в тестируемом наборе присутствуют некоторые истинные причинные взаимосвязи, их рейтинги значимости будут основаны на других распределениях (черные столбцы на том же рисунке). Можно применить это различие между наблюдаемым и ожидаемым, чтобы выяснить, какие значения меры могут считаться каузальными[259].

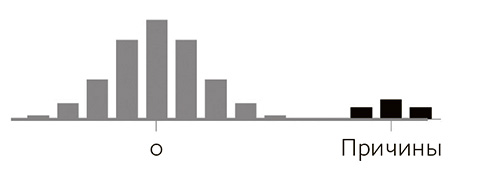
Рис. 6.9. Гистограмма рейтингов значимости для набора причинных зависимостей. Область светло-серого цвета (со средним значением 0, обозначающим незначимость) представляет ложные зависимости, черные столбцы – истинные причины. Из-за помех и иных факторов не все непричины будут иметь значимость 0, но будут распределены вокруг этой центральной области

Как обычно, чтобы высокие уровни причинной значимости соответствовали истинным причинам, нужно быть уверенными, что мы точно измерили силу (и, следовательно, вероятности репрезентативны относительно истинных значений) и, как в байесовских сетях, общие причины (или можно переоценить значимость других причин либо выявить ложные зависимости). Для этих временных рядов также понадобится сделать допущение, что отношения остаются стационарными во времени. Причина в том, что если отношения изменяются во времени, то, возможно, две переменные будут независимы для одной, но не для другой части временных рядов. Когда мы исследуем весь временной ряд сразу, отношения могут показаться слабыми, даже несмотря на их относительную силу на фоне некоторой части ряда.

Отвечая на вопрос «почему», мы часто забываем о вопросе «когда». В ряде методов можно уточнить временное запаздывание, или окно, так что нетрудно рассчитать значимость, скажем, близкого контакта с человеком, больным гриппом, для развития симптомов заболевания в период от одного до четырех дней. Но, если мы не имеем никакого понятия о том, что вызывает грипп, как поймем, что протестировали именно это «окошко»? Вот одно из слабых мест, присущих подобным подходам: если мы протестируем неверный набор временных рядов, то либо не сумеем выявить нескорые реальные причины, либо найдем только подгруппу в пределах истинного набора временных задержек.

Тестирование всех мыслимых запаздываний не слишком разумная стратегия, так как это значительно повышает сложность вычислений, при этом даже не гарантирует, что будут найдены правильные временные паттерны. Дело в том, что выборка данных часто берется неравномерно по времени и разброс может быть слишком велик (при малом количестве измерений и больших пробелах между ними), а пробелы не обладают свойством выборочного распределения.

Скажем, у нас есть результаты лабораторных испытаний для группы пациентов, а также врачебные предписания для них. Даже если лекарство однозначно повышает сахар в крови на протяжении недели, имеющиеся у нас измерения вообще (или в большей части) могли проводиться не сразу после приема препарата. Может также иметь место запаздывание от даты назначения до начала приема лекарства, так что кажущаяся длительная задержка между предписанием и повышением глюкозы на самом деле способна проявиться только через неделю после лечения. В результате для каждого отдельного временного интервала может не хватить объема наблюдений. Применение временных окошек может принести пользу (поскольку, если взять их вместе, удастся получить достаточное количество наблюдений за 5–10 дней), хотя по-прежнему не решается проблема с тем, какое именно временное окошко тестировать.

Один из способов выявления временных паттернов на основе данных – набирать потенциальные паттерны и потом корректировать, исходя из данных. Реальным этот метод делает мера значимости. Посмотрим на рис. 6.10, когда тестируемое временное окно перекрывает истинное, но отличается от него. Это и есть возможные сценарии. По мере того как окно растягивается, сужается или смещается, мы пересчитываем причинную значимость. В каждом случае, меняя некорректные окна, чтобы приблизиться к истинному, мы улучшаем рейтинг значимости. При наличии временного окна наша переменная-следствие и будет следствием, которое случается в некотором временном диапазоне. Если окно намного шире истинного, как на рис. 6.10, будет множество примеров, когда можно ожидать, что следствие произойдет, но этого не случится (следовательно, рейтинг значимости будет исключен для всех этих следствий, по видимости не случившихся после причины). С другой стороны, если окно слишком узкое, следствие будет казаться вероятным, даже когда не вызывается потенциальной тестируемой причиной. По мере того как временные паттерны приближаются к реальным, значимость возрастает, и можно доказать, что она соответствует действительной[260].

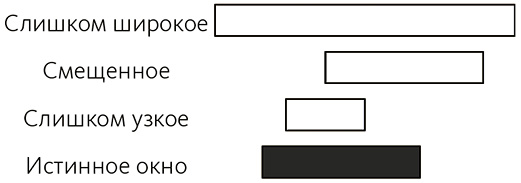
Рис. 6.10. Возможные случаи, когда временное окно причины при тестировании образует перехлест, но отличается от истинной причины, в которой производит следствие

Вероятности применяются чаще всего тогда, когда данные включают дискретные события: к примеру, наличие или отсутствие диагноза; лабораторные значения, сгруппированные по категориям «нормальное», «высокое» и «низкое». Но что, если требуется понять, как изменения в ценах на одну акцию приводят к модуляциям в объемах торгов другой ценной бумагой? Тогда на самом деле мы хотим выяснить не то, как одно ценовое значение приводит к росту объема торгов, а размеры ожидаемого роста.

В то время как вероятностные методы тестируют, насколько шансы того, что случится некое событие, меняются в зависимости от причины, мы также можем проверить, как меняется значение переменной относительно изменений в причине. Большинство методов, которые мы рассматривали до сих пор, доступны к использованию как раз подобным образом.

Хотя, строго говоря, традиционно это не считается каузальностью (по мотивам, которые мы вкратце рассмотрим), один из общеприменимых методов причинного осмысления на основе данных временных рядов с непрерывными значениями называется «причинность по Грэнджеру»[261]. Взяв за основу труды Винера (1956), который утверждал, что причины повышают предсказуемость следствий, Грэнджер разработал прикладной метод тестирования каузальности в финансовых динамических рядах, таких как прибыль от ценных бумаг. Идея в следующем: причина предоставляет некую информацию о следствии, которая не содержится в других переменных и позволяет лучше предвидеть значение следствия. И, если мы возьмем всю сумму знаний до определенного момента, вероятность того, что следствие имеет некоторое значение, будет отличаться, если мы удалим причину из этого набора сведений.

На практике мы не располагаем неограниченным набором информации и не можем использовать ее всю, даже если получим благодаря сложным вычислениям.

Не вдаваясь в детали, скажем: существуют две формы причинности по Грэнджеру, каждая из которых приводит к совершенно разным логическим заключениям. Важно понять, что ни та, ни другая по-настоящему не соответствуют причинности. Но, поскольку их часто применяют в поддержку каузальных утверждений, полезно разобраться, на что они способны, а на что нет.

Во-первых, двумерная причинность по Грэнджеру ненамного отличается от корреляции (хотя сама мера несимметрична). Она включает всего две переменные и просто сообщает, может ли одна помочь в прогнозировании другой. Так, если мы измеряем погоду, задержки авиарейсов и продажи кофе в аэропорту, то в состоянии выявить зависимости только между парами, например прогнозируя задержки авиарейсов по погоде. Даже если нет скрытых переменных, такой подход не дает никаких преимуществ для предотвращения искажений. Таким образом, двумерная причинность по Грэнджеру иногда приводит к обнаружению ложных мотивационных взаимосвязей между следствиями с общей причиной. Если плохая погода вызывает задержки отправления и самолетов, и поездов, мы можем некорректно заключить, что отложенные авиарейсы оказываются причиной запаздывания железнодорожного транспорта, и наоборот. В соответствии с этим методом легко сделать вывод, что все до единого более ранние звенья в цепочке причин становятся поводами для более поздних, вместо того чтобы выявить только непосредственные взаимосвязи. То есть если у нас есть последовательность событий, можно решить, что первое есть причина последнего, поскольку мы не принимаем в расчет промежуточные звенья.

Есть множество методов тестирования причинности по Грэнджеру, однако самый простой из них – регрессия. Скажем, требуется выяснить, что было вначале – курица или яйцо. Следуя Турману и Фишеру[262] (1988), возьмем два временных ряда: один будет показывать ежегодное производство яиц, а другой – годовую популяцию кур. В итоге получим два уравнения: одно покажет зависимость значений по курам от предыдущих значений и кур, и яиц, а другое – зависимость яиц от предыдущих значений по курам и яйцам. Количество предыдущих значений (интервалов) – это параметр, который выбирает пользователь.

Здесь возможен тест на зависимость между производством яиц в определенный год и популяцией кур в предыдущий год, два и т. д. Для каждого года производства яиц и популяции кур существует коэффициент, показывающий, насколько значение текущего года зависит от показателя предыдущего. Нулевой коэффициент означает отсутствие зависимости вообще. Итак, если коэффициенты производства яиц в уравнении для яиц отличны от нуля в некоем временном интервале, тогда куры – это грэнджеровская причина яиц (если значение для предыдущего года – два, это значит, что яйца в два раза превышают популяцию кур за предыдущий год).

Чаще всего увеличение интервалов означает повышение сложности, также может устанавливаться практический предел для тестирования, помимо ограничений, связанных с данными, например количество точек данных и детализация измерений.

Вернемся в наш аэропорт. Скажем, при прогнозировании продаж кофе мы возьмем в качестве переменных погоду, задержки вылетов и предыдущие значения продаж кофе. Это будет многомерная причинность по Грэнджеру, когда мы включаем в каждый тест все имеющиеся переменные. Нет возможности принять во внимание все сведения в мире, но нетрудно проверить, будет ли информативна некоторая переменная, если учтены все остальные, оказавшиеся в нашем распоряжении. Скажем, истинная зависимость такова: погода вызывает задержки рейсов, а задержки рейсов вызывают рост продаж кофе, потому что людям приходится ждать в аэропорту. Тогда, после включения в кофейное уравнение задержки, погода не сможет дать никакой новой информации, и ее коэффициент будет стремиться к нулю (а значит, не повлияет на прогнозирование объема продаж кофе). Нельзя утверждать, что наблюдается причинная взаимосвязь, поскольку коэффициенты все же отличны от нуля, однако нетрудно провести тесты и проверить статистическую значимость этого отличия от нуля.

Здесь мы подходим ближе к причинности, но нет гарантии, что наши выводы истинны. Что еще важнее, даже если многомерная форма гораздо сильнее и точнее, она применяется намного реже, поскольку требует слишком интенсивных вычислений[263].

Оглавление книги