Книга: Почему

Графические модели

Графические модели

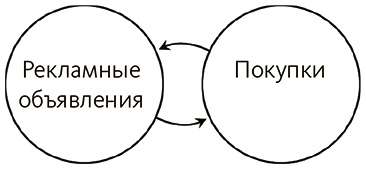
Нередко, пытаясь описать причинные взаимосвязи кому-то другому или понять, как вещи работают вместе, мы рисуем картинки. Такие изображения можно соотнести с вероятностными теориями причинности, которые разрабатывают философы. Взглянем на рисунок ниже, где показано, как вероятность одной переменной зависит от другой.

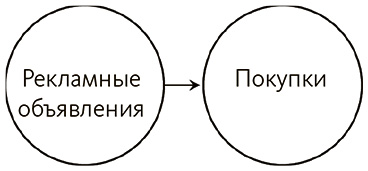
Прежде всего видно, что между рекламными объявлениями и покупательским поведением есть взаимосвязь. Мы знаем, что эта взаимосвязь действует в одном направлении – реклама влияет на покупки, а не наоборот.

А теперь добавим переменную.

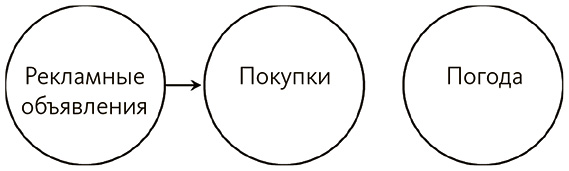
Если мы захотим предсказать, будет ли совершена покупка, что нам требуется? Способ взаимосвязи переменных говорит: все еще необходимо знать лишь о том, видел ли некто рекламу. Визуально погода стоит справа особняком, а отсутствие ориентированного ребра (стрелки) от погоды к покупке означает, что этот фактор нельзя использовать для воздействия или предсказания предполагаемого следствия.

Идея о том, что для прогнозирования переменной нужно знать только о прямых ее причинах, называется причинным условием Маркова[236]. Говоря технически, переменная не зависит от своих «непотомков» («потомки» – это следствия, следствия следствий и т. д.) при условии наличия их причин[237]. Здесь ребра идут от причины к следствию, поэтому прямые причины – те, что связаны со следствием стрелкой.

Чтобы наглядно продемонстрировать полезность этой идеи, добавим причину рекламных объявлений.

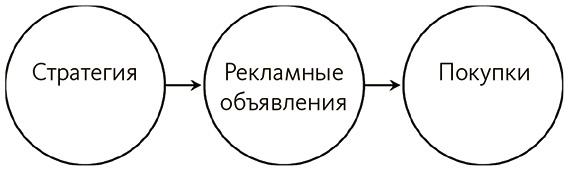
Если маркетинговые стратегии влияют на покупки только посредством рекламы, то и вероятность покупки зависит лишь от рекламы – ее прямой причины. Как только значение объявления установлено, причина его появления теряет важность. Даже если мы обнаружим множество других причин объявлений, это не изменит фактора информации, которая нужна для прогнозирования покупок, так как все воздействия других переменных работают через объявления.

Перейдем к следующему рисунку.

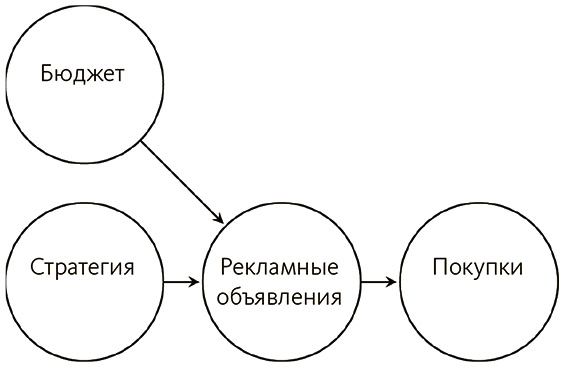
Если мы захотим что-нибудь узнать о статусе покупок, не нужно выяснять, были ли объявления частью спланированной кампании или просто запущена массированная реклама. Чтобы понять, совершится ли покупка, важно лишь знать о факте показа рекламных объявлений. Эта идея аналогична скринингу, который мы наблюдали в главе 5. В теории это говорит о том, что если мы в силах прямо воздействовать на рекламу, никак не меняя при этом маркетинговые стратегии или бюджет, увидим и изменение в покупках. Дело в том, что они полностью определяются тем, как мы установим значение рекламных объявлений. На деле, однако, может оказаться невозможным вмешаться только в одну переменную, независимо от остальных на рисунке (подробнее об этом в главе 7). Рекламу нельзя включить и отключить по мановению волшебной палочки, а вмешательства порой провоцируют непредвиденные побочные эффекты.

Рисунки такого вида не могут отобразить все возможные зависимости. Увеличение покупок также может приводить к расширению рекламы или к изменению стратегии, а это создает на изображении цикличность. Предложенные здесь иллюстрации – это графический режим представления данных, известный как байесовские сети[238],[239], а именно тип ориентированных и ациклических графов[240]. «Ациклический» означает всего лишь отсутствие петель на графе, так что нижеследующее недопустимо.

Если представить, что вы прокладываете себе путь через ациклический граф, то закончить маршрут в том узле, с которого вы начали, невозможно. Такое свойство оказывается до удивления важным, когда мы применяем эти структуры в целях упрощения вероятностных расчетов. Скажем, требуется узнать вероятность одновременно покупок и рекламы, и мы ограничимся простым случаем, когда и то и другое может быть истинным или ложным. В отсутствие цикла, когда есть только ориентированное ребро (стрелка) от рекламы к покупкам, вероятность обоих событий вместе становится простой вероятностью покупки при условии рекламы, помноженной на вероятность того, что реклама истинна[241]. То есть поскольку покупки зависят только от рекламы, просто нужно знать вероятность покупки, если известно, что реклама истинна, а затем учесть вероятность того, что происходит в действительности. К примеру, если вероятность покупки после просмотра рекламы составляет 1, но реклама имеет более низкую вероятность – скажем, 0,01, – шанс увидеть то и другое вместе будет равен 0,01.

Но если между двумя факторами есть петля обратной связи, вероятность рекламы также зависит от вероятности покупки. Это затрудняет расчеты, если мы хотим, чтобы воздействие случилось одновременно, однако проблему можно решить, добавив фактор времени.

Скажем, покупка в некоторый момент времени воздействует на рекламу с запаздыванием, не моментально. Чтобы это представить, понадобится множество графов.

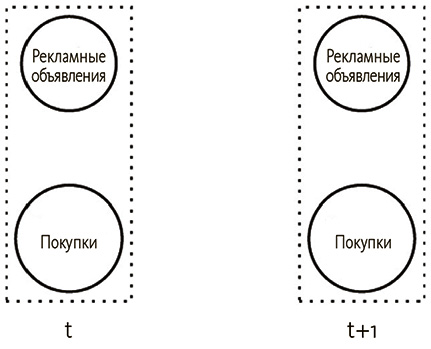
Здесь мы имеем один граф, где показано, как переменные связаны по времени t, и еще один для следующего за этим момента времени t + 1. Реклама и покупки разобщены на каждом графе, поскольку не оказывают немедленного воздействия друг на друга. Каждый из графов для отдельных временных сегментов представляет собой байесовскую сеть и, следовательно, не может иметь циклов. Однако мы можем получить моментальное следствие между рекламой и покупкой или наоборот, поскольку на одном графике и то и другое присутствовать не может. Вместо этого соединим графы по времени, чтобы отобразить обратную связь.

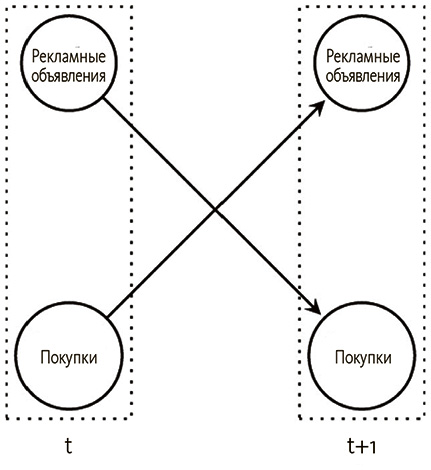
Затем эта структура неоднократно повторится во времени, так что каждый раз покупка будет зависеть от значения рекламы в предыдущий раз, и наоборот.

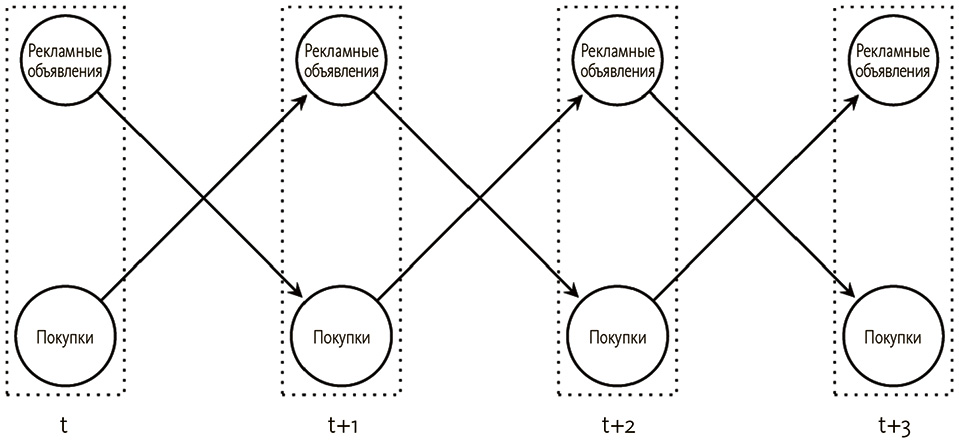
Такой граф называется динамической байесовской сетью, хотя сама структура фактически неизменна во времени[242].

Возможны более сложные структуры со множественными задержками по времени, и необязательна связь со следующим моментом на временной шкале. Задержки могут быть и более долгими (например, запаздывание между подверженностью вирусу и развитием симптомов). Главное возражение – сложность осмысления таких структур существенно возрастает по мере увеличения числа переменных и задержек по времени.

Мы можем использовать графы для представления причинно-следственных связей, но это не значит, что каждый граф, который мы создаем или о котором узнаём, имеет характер причинности. До сих пор мы всего лишь изображали, как вероятность одной вещи зависит от вероятности другой. Мы могли с такой же легкостью получить графы, показывающие, как перейти от аудиохарактеристик к распознаванию речи, фильтровать спам на основе его содержания и идентифицировать лица на изображениях. Может существовать множество графов, соответствующих набору вероятностных отношений (то есть представляющих тот же набор зависимостей).

Так как же узнать, каузальна ли графическая модель? Ответ кроется прежде всего в допущениях, связывающих графы с теориями, о которых мы уже говорили.

Первые графические модели причинных умозаключений были разработаны философами (Спиретс и др.) и специалистом по информационным технологиям (Перл), которые объединили философию причинности с графическими моделями. Скажем, реклама есть причина одновременно покупок и узнаваемости бренда, как на рис. 6.4 (а). Если бы у нас не было переменной, представляющей рекламные объявления, и мы пытались вывести зависимости из набора данных, то обнаружили бы граф на рис. 6.4 (б), где некорректно показаны покупки в качестве причины узнаваемости бренда.

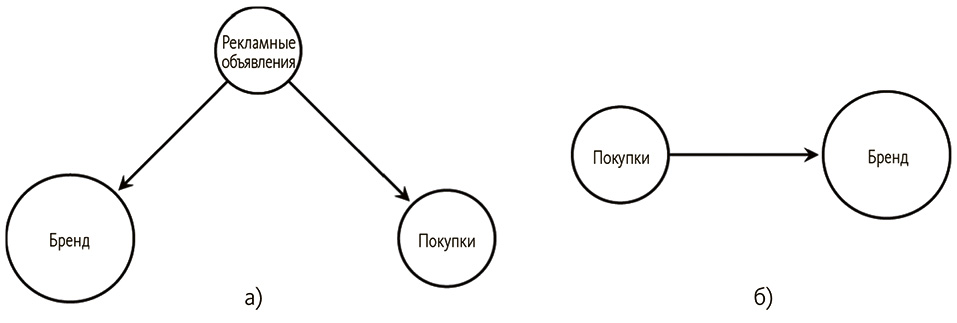
Рис. 6.4. Истинная структура показана слева. Если реклама не наблюдаемая переменная, может появиться некорректная структура справа

Вспомните допущение об отсутствии скрытых общих причин, или о каузальной достаточности, из начала этой главы. Она необходима, чтобы избежать подобных ошибок. В целом может присутствовать общая причина любого ряда переменных, и, если она не измерена, мы не можем быть уверены, что результирующие выводы о каузальности окажутся корректны.

А что будет, если наша рекламная переменная указывает, действительно ли было куплено рекламное время на ТВ, но истинная причина – это просмотр рекламы определенное количество раз?

Как уже говорилось, нам нужны правильные переменные. Каузальные взаимосвязи могут включать в себя сложные их наборы: если выкурить одну сигарету, это вряд ли приведет к раку легких, но многолетнее курение – уже более сильная причина; лекарства часто имеют порог токсичности, так что 5 мг препарата могут не вызвать опасных последствий, а вот 50 мг – уже смертельная доза; грейпфрут не вреден, но он взаимодействует со многими лекарствами, вызывая серьезные побочные эффекты. Если к числу переменных относится факт курения (а не его продолжительность), факт приема лекарства (а не доза) и потребление грейпфрутов (а не их потребление на фоне приема определенного лекарства), то можно не найти причинных зависимостей или определить их неверно.

Такие структуры представляют собой вероятностные отношения и сообщают, какие переменные необходимы для прогнозирования значения остальных, однако для фактического расчета вероятности требуется еще один элемент информации.

Байесовская сеть состоит из двух частей: это структура (то есть как именно связаны между собой переменные) и набор распределения условных вероятностей. Если не слишком вдаваться в детали, это всего лишь таблицы, которые позволяют узнать вероятность каждого значения переменной, исходя из значений ее причин. Для простого графа с рекламой и покупкой хватит двух рядов и двух колонок.

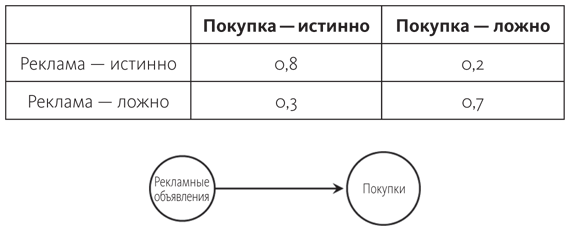
Сумма каждого ряда составляет 1, поскольку, независимо от значений, которые принимает реклама, покупка также должна иметь некое значение, а сумма вероятностей равняться 1. Колонки не суммируются до единицы, потому что они дают вероятность конкретного значения покупки при условии двух значений рекламы. Наш простой граф не завершен, так как для него нужна еще одна таблица с вероятностью рекламы. То есть теперь известно, как определить вероятность покупки с учетом значения рекламы; но как выяснить вероятность рекламы? В этой таблице будет только два числа, поскольку у рекламы в графе нет родительских переменных, и ее вероятность ни от чего не зависит (точно так же вероятность того, что бросок монеты будет иметь конкретное значение, обычно не зависит от значения другой переменной).

Для каждого узла в сети мы получим аналогичную таблицу. Знание структуры существенно упрощает расчеты, так как значение каждой переменной задается ее исходными переменными. Напротив, если мы ничего не знаем о связи между переменными, нам придется включить их все в каждую строку таблицы. Если есть N переменных, которые могут быть истинными или ложными, количество строк будет равняться 2N. Мы можем получить знание о структуре и вероятностях из имеющихся данных или создать структуру на основе уже известного и отсюда выяснить вероятности.

В обоих случаях, однако, мы должны быть уверены, что данные корректно представляют истинные зависимости между переменными. Это возвращает к допущению о репрезентативном распределении, или верности. К примеру, мы не получим варианта, когда реклама способствует покупкам только в одном направлении, но мешает, если они ведут, скажем, к усталости от принятия решений. Если такое случится, мы можем не увидеть зависимости между рекламой и покупками, даже если это присутствует в истинной структуре. Мы также можем не найти правильных вероятностей, если на графе мало точек.

Верность может не иметь места в ряде других случаев, например при парадоксе Симпсона. Или когда в зависимости от разделения данных (например, все пациенты против только мужчин или только женщин) мы могли наблюдать независимость, а в действительности ее не было (например, больше женщин принимали лекарство А, чем лекарство B) и результаты отличались (например, у женщин были лучше, чем у мужчин, независимо от лекарства).

Еще один проблематичный случай – детерминизм взаимосвязей. Скажем, каждый раз, когда приходит электронное сообщение, компьютер подает сигнал, который, в свою очередь, заставляет моего пса лаять.

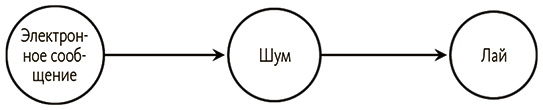
Если вероятность лая при условии сигнала равна 1 и вероятность сигнала при условии электронного сообщения также равна 1 (так что оба события происходят, когда имеют место их причины), сигнал не приводит к независимости сообщения и лая, даже если согласно структуре это должно происходить.

Представьте, что вам известно только, получено сообщение или нет. Теперь вы также знаете статус других переменных, потому что, если есть сообщение, сигнал также звучит и ведет к лаю. Вы можете некорректно заключить, что сообщение напрямую становится причиной других переменных. Эта проблема, однако, свойственна не только графическим моделям, а вообще большинству вероятностных методов.

Итак, повторим. Причинность графическим моделям придают следующие допущения.

• Вероятность переменной зависит только от ее причин (причинное условие Маркова).

• Все общие причины измерены (достаточность).

• Данные, на основе которых мы получаем знание, точно представляют реальные зависимости (верность).

Есть и другие неявные допущения, обеспечивающие корректность причинно-следственных заключений (должно быть достаточно данных, переменные должны быть корректно представлены и т. д.), но три вышеназванных допущения чаще всего становятся предметом обсуждений и отражают основные различия между графами, которые представляют и не представляют причины.

Скажем, о сотрудниках компании есть некоторые данные: о рабочих часах, отпусках, о производительности и тому подобное. Как найти сеть причинно-следственных связей между ними?[243]

Один из подходов – разработать меру для описания данных моделью, найти все возможные модели и выбрать одну с лучшим результатом. Это методы поиска и оценки[244]. Допустим, в массиве данных истинно единственное отношение: «отпуск есть причина продуктивности». Значит, модель с этим ребром должна иметь балл выше, чем имеющая и другие отношения или в которой это ребро направлено в обратную сторону (от продуктивности к отпуску). То есть граф на рис. 6.5 (а) должен иметь более высокую оценку.

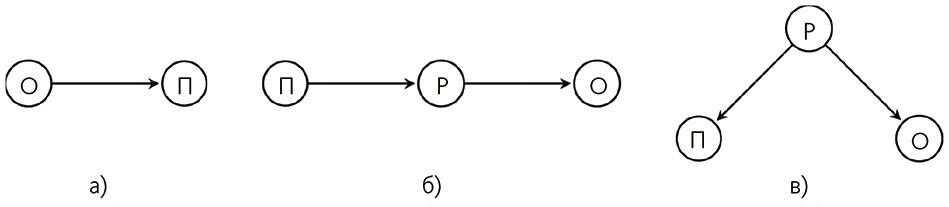
Рис. 6.5. Если О ? П, первый граф будет иметь самую высокую оценку

Имея только эти три переменные, можно перечислить все возможные графы, проверить каждый и сделать выбор. Но, чтобы выбрать, нужен способ рассчитать, какой из них лучше соответствует данным. Есть много оценочных функций[245], и в итоге всегда выявляется, насколько хорошо мы описываем данные, не подстраивая граф под помехи и специфические свойства конкретного набора. Мы можем идеально учесть каждую точку в наборе данных с очень сложной структурой, но, вместо того чтобы моделировать каждый бит помех, стоит найти модель, которая охватывает более общие взаимосвязи между ее переменными.

Итак, обычно имеется фактор, исключающий граф, когда тот становится слишком сложным. Однако мы не можем выбирать между всеми возможными графами. Для набора из 10 переменных существует более 10¹⁸ вероятных графов[246]. Это более чем в миллион раз превышает количество американской валюты[247]. При этом не стоит даже пытаться искать взаимосвязи между всеми акциями в индексе S&P 500[248]. Всего при 25 переменных количество возможных графов (свыше 10¹¹⁰) оставляет далеко позади число атомов во Вселенной (по прикидкам, их сравнительно мало – 10⁸⁰)[249]. Ни при каких обстоятельствах нельзя протестировать их все, однако на практике это и не требуется. Мы можем выборочно сгенерировать столько, сколько возможно, и выбрать лучший, хотя с учетом их количества вряд ли вероятно, что мы натолкнемся как на раз на нужный. Вместо этого для алгоритмов проще задать некоторые индикаторы важности графов.

Скажем, мы тестируем первые три графа на рис. 6.6: рис. 6.6 (в) имеет высший рейтинг. Тогда наилучшая стратегия – не выборочное генерирование четвертого графа, а исследование ближних к нему. Мы можем добавить ребро, изменить его направление или удалить и посмотреть, как изменится рейтинг. Тем не менее может случиться так, что лучшим графом окажется изображенный на рис. 6.6 (г) и мы не сможем протестировать его с помощью этой стратегии, поскольку доводим до оптимума третий граф и останавливаемся еще до получения истинной структуры. Но, не тестируя каждый граф, нельзя узнать наверняка, что лучший из них попал в диапазон проверки.

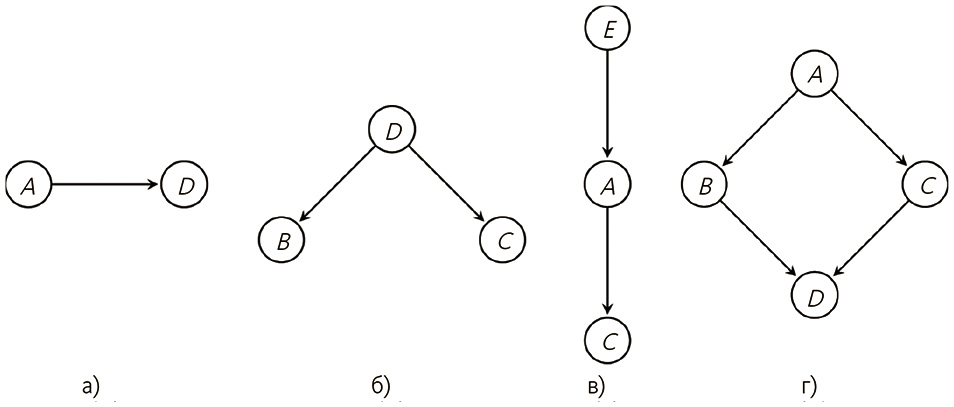
Рис. 6.6. При переменных А, В, С и D рисунки а – в отображают возможные графы для тестирования. На рисунке г показана истинная структура

На рис. 6.7 проиллюстрирована проблема локальной оптимизации. Если ось Y – это рейтинг графа и мы тестируем только графы рядом с отмеченной точкой, можно думать, что это лучший из возможных рейтингов, потому что он самый высокий. Это называется «застрять в локальном оптимуме», потому что мы оптимизировали рейтинг в конкретной области. Но это не лучший из возможных результатов.

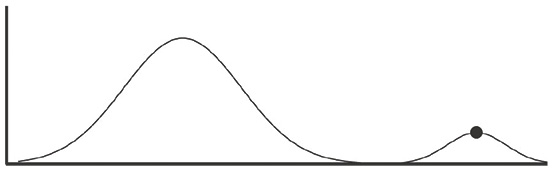
Рис. 6.7. Иллюстрация локального оптимума

Чтобы разрешить эту проблему, в алгоритмах изучения причинных структур используются «умные» методы ограничения набора графов, которые необходимо протестировать, и исследования максимально большего поискового пространства. К примеру, если нам известно, что пол – это всегда причина, но никогда не следствие, можно избежать тестирования графов, показывающих следствия.

Если у нас есть представление о видах вероятных структур, можно сгенерировать вероятностное распределение на основе набора графов и с его помощью сориентироваться по поводу возможных структур для исследования[250].

Как вариант, вместо изучения устрашающе огромного набора потенциальных графов можно использовать зависимости между переменными для построения графа. Методы на основе ограничений предназначены именно для этого: для тестирования по критерию независимости и применения результатов, чтобы добавлять, удалять или ориентировать ребра графа.

Одни методы предусматривают добавление переменных по очереди, а другие начинают со связывания всех переменных друг с другом и удаления ребер по одному[251].

Возьмем следующий граф, где три переменные соединены всеми возможными путями.

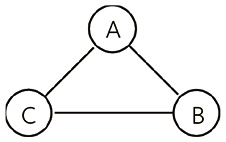
Если мы обнаружим, что А и В независимы при условии С, сможем удалить ребро между ними и продолжить поиск иных взаимосвязей, позволяющих так же снимать ориентировочные ребра. Порядок тестирования, однако, имеет значение, поэтому ошибка на первых шагах может привести к заблуждениям в последующих. Имея реальные данные, вряд ли можно обнаружить точную независимость, однако придется решить, в какой точке принять или отвергнуть гипотезу. То есть, если вероятность А при условии В в точности равна вероятности А, имеет место их независимость. Однако можно обнаружить, что вероятность А при условии В и С очень близка к вероятности только при условии С, но не равна ей.

На практике необходимо выбирать статистический порог, чтобы принять заключение об условной независимости на основе таких тестов. И если необходимо провести большое количество тестов, мы столкнемся со множеством проблем по проверке разнообразных гипотез, о которых говорилось ранее (вспомните эксперимент с дохлым лососем)[252].

Оглавление книги