Книга: Почему

Допущения

Допущения

Прежде чем переходить к методам причинного осмысления, нужно дать некоторые вводные сведения. Под термином «причинное осмысление» я имею в виду следующее. Набор измеримых переменных (например, исторические цены на акции) закладывается в компьютерную программу. На основе обработанной информации делается вывод, какие переменные оказались причиной других (к примеру, рост цен на акцию А вызывает рост цен на акцию B). Это может означать выявление силы взаимоотношений в каждой паре переменных или выяснение модели их взаимодействия. Данные могут быть временной последовательностью событий (к примеру, дневные изменения цен на акции) или взятыми на конкретный момент. Во втором случае вариация берется в пределах неких выборок вместо изучения временных изменений. Один из примеров такого рода данных – одномоментное исследование группы, а не экспертное отслеживание отдельных участников в течение долгого времени.

Допущения для различных методов слегка варьируются по критерию используемых данных, однако некоторые свойства оказываются общими практически для всех методов и влияют на любые заключения.

Вероятно, самое важное и универсальное допущение звучит так: все общие причины переменных, зависимости между которыми мы рассматриваем, измеримы. Это также называют причинной достаточностью в методах графических моделей (к ним мы вскоре перейдем).

Если мы, имея набор переменных, хотим найти между ними каузальные зависимости, то должны быть уверены, что уже измерили все общие причины этих переменных. Если истинно утверждение, что кофеин приводит к недосыпанию и повышает давление – и что это единственная взаимосвязь между сном и сердечным ритмом, – то, не измерив потребления кофеина, мы можем сделать некорректные выводы при выявлении отношений между его следствиями. Причины, отсутствующие в наборе данных, называются скрытыми или латентными переменными. Неизмеренные причины двух или более переменных, способных привести к ложным умозаключениям, именуются скрытыми общими причинами или латентными искажающими факторами, а возникающие вследствие этого проблемы называются искажением (что чаще встречается в информационных технологиях и философской литературе) и смещением из-за пропущенных переменных (что более присуще статистике и экономике). Это одно из ключевых ограничений исследований наблюдением, а также вводных данных в вычислительных методах, поскольку приводит как к выявлению ложных взаимосвязей, так и к переоценке силы причин.

Немного изменим этот пример. Кофе напрямую влияет на сон – а теперь он будет влиять на сон и через фактор частоты сердечных сокращений (ЧСС), как на рис. 6.1. Даже если ЧСС служит причиной недосыпа, мы видим, что этот фактор более/менее значим, чем если бы мы не измеряли потребление кофе. То есть, поскольку кофеин вызывает сердцебиение, высокий показатель последнего может дать нам некую информацию о статусе тонизирующего напитка (присутствие/отсутствие). В главе 7 мы увидим, как экспериментальными методами посредством рандомизации[230] можно решать эту проблему.

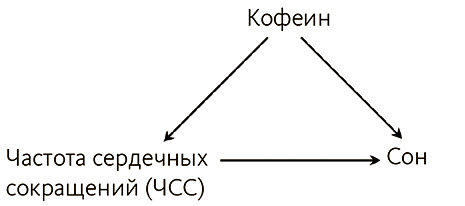
Рис. 6.1. Кофеин – общая причина учащения пульса и недосыпания, однако ЧСС также напрямую влияет на сон

Хотя практически любой метод, основанный на данных наблюдения, допускает, что нет никаких скрытых общих причин, на практике редко можно быть уверенным в этом. Заметим, однако: мы не обязаны допускать, что измерена каждая причина – только общие.

На рис. 6.2 (а) показано, что кофеин изменяет как качество сна, так и сердечный ритм; алкоголь вызывает аналогичный эффект. Не располагая данными по потреблению алкоголя, мы не сумеем выявить эту причину изменений сна, однако в результате не будут сделаны некорректные выводы об их взаимоотношениях. Аналогично, если кофе воздействует на сон посредством промежуточной переменной, отношения будут примерно такими: кофеин вызывает повышенное сердцебиение, а оно провоцирует недосып (рис. 6.2 (б)), и если при этом мы не измеряем сердцебиение, то просто найдем более неявную причину, а не некорректную структуру. Таким образом, необязательно наблюдать каждое индивидуальное звено в каузальной цепи.

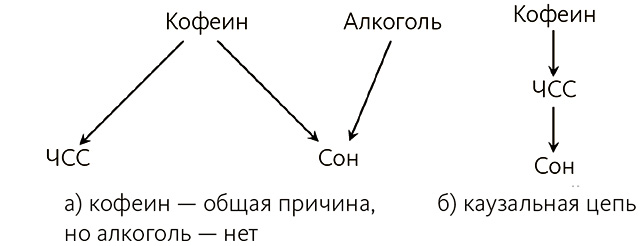
Рис. 6.2. Если алкоголь (слева) и сердцебиение (справа) не измерены, это не ведет к искажению связи между кофеином и сном

Некоторые вычислительные методы исходят из допущения, что все общие причины измерены, и определяют, в каких случаях может существовать невыявленная причина, или иногда помогают обнаружить саму причину. Однако это, как правило, возможно только при очень жестких условиях и затруднительно при наличии комплексных временных рядов[231]. Но как быть, если мы не знаем, что все общие причины измерены, и не в состоянии применить эти методы для выяснения причин?

В методах графических моделей, о которых мы поговорим далее, доступно только одно: найти все возможные модели, соответствующие данным, включая те, которые имеют скрытые переменные.

К примеру, если мы найдем видимую причинную зависимость между сном и сердцебиением и при этом будем знать, что могут существовать неизмеренные причины обоих факторов, то одной из возможных моделей будет скрытая переменная, которая вызывает оба наблюдаемых фактора. Преимущество в том, что иногда возникают некие общие для всех моделей взаимосвязи, объясняющие имеющиеся данные. Тогда, даже когда есть множество возможных структур, нетрудно вывести некие заключения относительно потенциальных корреляций.

Во всех случаях, однако, уверенность в выводах о каузальных взаимосвязях должна быть пропорциональна убежденности, что нет никакой потенциально неизмеренной причины, а заключение, сделанное на основе данных наблюдения, может стать точкой отсчета для будущих экспериментов, которые подтвердят его или опровергнут.

Помимо уверенности, что мы располагаем верным набором переменных, необходимо также знать, что наблюдаемые события отражают истинное поведение системы. По существу, если нет сведений, что наличие тревожной сигнализации становится причиной ограблений, нужно верить, что – при наших данных – ограбления зависят от отсутствия системы сигнализации.

Мы уже изучили несколько ситуаций, когда сведения не были репрезентативными: 1) анализ данных в ограниченном диапазоне не позволил выявить корреляции между интенсивностью учебы и экзаменационными баллами (глава 3); 2) парадокс Симпсона стал причиной исчезновения или обращения вспять причинно-следственных связей между лекарствами и исходом заболеваний в зависимости от того, брались данные агрегированно или изучались отдельно для мужчин и женщин (глава 5).

Также мы видели пример, как можно нивелировать взаимозависимости, чтобы выявлять причинности без корреляций. В главе 3 мы наблюдали две цепочки между занятиями бегом и потерей веса, когда бег давал положительный эффект и отрицательный, поскольку занятия спортом вызывали повышенный аппетит. При неудачном распределении это значит, что мы можем вообще не обнаружить никакой взаимосвязи между пробежками и потерей веса. Поскольку осмысление причинности зависит от наблюдения реальных зависимостей, мы, как правило, вынуждены делать допущение, что такого типа нивелирования нет. Подобное допущение часто называют верностью (речь о видах ассоциации), поскольку данные, не отражающие истинную структуру, на которой все построено, в некотором смысле ей «неверны».

Кое-кто утверждает, что такой тип нарушения связи редок[232], но на деле некоторые системы – к примеру, биологические – структурированы так, что практически гарантируют нарушение. Когда множественные гены продуцируют фенотип, даже если мы возьмем за основу неактивный ген, фенотип по-прежнему будет присутствовать, что приведет к видимой зависимости между причиной и следствием. Многие системы, вынужденные поддерживать равновесие, включают подобного рода резервные причины.

И все же нам даже не нужна точная нивелировка или вообще какая-либо зависимость, чтобы нарушить допущения о верности. Это потому, что на практике большинство вычислительных методов требует выбирать статистический предел, на основании которого зависимость будет принята или отвергнута (здесь используются p-значения или другие критерии). Вероятность следствия не должна быть в точности равна его вероятности под условием причины – просто достаточно близка, чтобы результат оставался в пределах допустимого. Например, вероятность потери веса после пробежки может не равняться вероятности потери веса вообще, без бега, однако может привести к нарушению допущения о верности, если отличие будет незначительным[233].

Еще один вариант нерепрезентативности распределения, касающегося истинного набора зависимостей, – смещение выборки. Скажем, есть данные из больницы, куда включены диагнозы и результаты лабораторных испытаний. Однако один из тестов крайне дорогой, поэтому врачи просят сделать его только в том случае, если у пациента необычная картина болезни и другим способом диагноз поставить нельзя. В большинстве случаев тест дает положительный результат. Из этих наблюдений, однако, нельзя узнать истинную вероятность такого исхода, потому что тест заказывают только при высоких шансах на положительный ответ. По результатам медицинских проверок мы, как правило, видим лишь ограниченный диапазон данных – например, когда измерения делаются только у самых больных пациентов (как инвазивный мониторинг в отделении интенсивной терапии). Диапазон наблюдаемых значений включает заболевших, состояние которых достаточно плохое для проведения подобного мониторинга. Ситуация проблематичная, поскольку это значит, что, если мы выявим причинную зависимость для такой ограниченной группы, она может не быть истинной для населения в целом. Аналогично можно не распознать истинную зависимость из-за отсутствия в выборке вариации.

Это называется проблемой упущенных данных. К искажению могут приводить упущенные переменные, но и упущенные измерения действуют аналогично, формируя нерепрезентативные распределения относительно истинного базового распределения. Упущенные значения, как правило, не результат случайного их удаления из набора данных, скорее, они зависят от других измеренных и неизмеренных переменных.

К примеру, в больнице для проведения медицинской процедуры у пациента нужно отключить несколько мониторов (что приведет к пробелу в регистрации сведений), или данные не зафиксируются из-за сбоя аппаратуры. Возможно, сахар в крови будет замеряться с меньшими интервалами, если этот показатель выходит за пределы нормы, поэтому большие пробелы в измерениях не окажутся независимыми от фактических значений, а существующие значения могут отклоняться вплоть до экстремумов. Данные, упущенные из-за скрытой причины, способны вести к искажениям, в то время как сбой аппаратуры может означать, что и другие близкие измерения также ложны (и могут искажать результаты).

В действительности мы только допускаем, что распределения отражают истинную структуру, поскольку размер выборки становится достаточно большим. Если я звоню другу и в этот момент раздается звонок в дверь, трудно сказать, повторится ли снова эта ситуация. Но что если это случается 5 или 15 раз? В общем, мы допускаем, что по мере увеличения массива данных мы все ближе подходим к наблюдению истинного распределения событий. Если бросить монетку всего несколько раз, можно не увидеть равного распределения орлов и решек; но по мере того, как число бросков будет стремиться к бесконечности, распределение приблизится к соотношению 50/50. Здесь увеличение массива данных означает снижение вероятности необычной цепочки событий, которая не будет отражать истинные базовые вероятности (такие как последовательность бросков игральных костей, когда выпадают одни шестерки).

Мы делаем аналогичное допущение для причинного осмысления: у нас достаточно данных, и мы можем усмотреть реальную вероятность (а не аномалию) того, что следствие наступает после причины. Нетрудно возразить, что для некоторых систем, например нестационарных, даже бесконечно большой набор данных может не удовлетворять этому допущению, и стоит исходить из предположения, что со временем отношения останутся стабильными. Вспомним: термин «нестационарные» означает, что свойства (например, средняя дневная прибыль от ценной бумаги) со временем меняются. На рис. 6.3 скидки (временные ряды обозначены пунктиром) и покупки горячего шоколада (сплошные линии) фактически не коррелируют по составным временным рядам, однако сильно взаимосвязаны в период, показанный серым цветом (который обозначает зимний сезон).

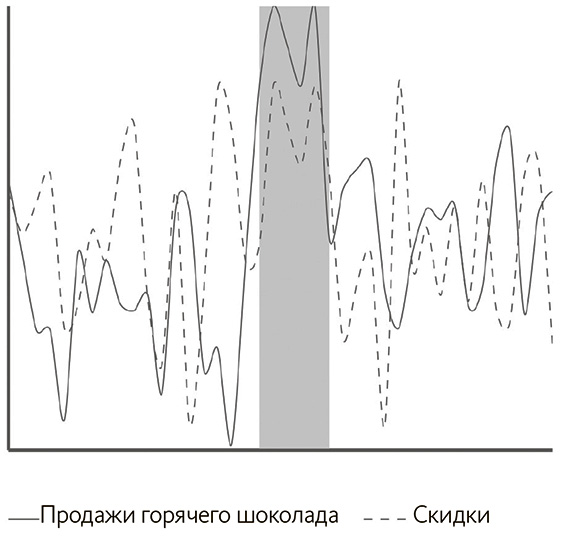
Рис. 6.3. Зависимость между двумя переменными со временем меняется, и они связаны только в период, обозначенный серым

Итак, если бы мы использовали все данные, то не выяснили бы, что скидки ведут к росту продаж горячего шоколада. Но, если бы воспользовались только сведениями по зимнему сезону, могли бы найти сильную зависимость. Стоит отметить, что увеличение объема данных не решает проблему – делать это нужно другими способами, о которых мы говорили в главе 4[234].

Задача большинства методов, основанных на логических выводах, – найти зависимости между переменными. Если вы располагаете данными по финансовым рынкам, переменными будут отдельные ценные бумаги. В политологии ими могут быть дневные пожертвования в фонд политической кампании или количество телефонных звонков.

Мы можем либо начать с набора уже измеренных факторов, либо провести некоторые измерения, и обычно мы считаем каждый измеренный фактор переменной. Однако есть некоторая неопределенность: нужно не только измерить правильные вещи, но и быть уверенными в их верном описании.

Помимо простого решения, включить в массив некие данные или нет, придется сделать множество выборов относительно организации самой информации. В рамках некоторых исследований обычное ожирение и патологическое (морбидное) могут входить в одну категорию понятий (и мы просто фиксируем, истинны эти состояния или нет для каждого человека). Но в исследованиях, посвященных лечению пациентов с ожирением, различие может оказаться критическим[235].

Измерение веса дает набор численных значений, которые заносятся на карту категорий. Возможно, самое важное здесь не вес, а то, меняется ли он, и если да, как быстро. Тогда вместо использования первичных данных о весе можно вычислить дневные или недельные отличия. Каково бы ни было решение, оно изменит результаты, поскольку они всегда относительны с точки зрения набора переменных. Если удалить некоторые переменные, может оказаться, что другие причины приобретут видимую значимость (например, снятие резервной причины может придать оставшейся больше видимой силы), а если добавить, то значимость других может снизиться (например, дополнительная общая причина может удалить ошибочную зависимость между следствиями такой причины).

Вернемся к примеру из начала главы, когда два медикамента по отдельности не повышали содержание сахара в крови, но иногда, принятые вместе, оказывали значительное воздействие на этот показатель. Вывод о причинной зависимости между отдельными переменными и разнообразными физиологическими измерениями, к примеру глюкозы, может помешать выявлению связи, но, если взять пару переменных вместе, удастся обнаружить неблагоприятное следствие. В этом случае правильная переменная – наличие двух медикаментов. Ее определение может быть проблематичным, но это единственная причина, по которой можно упустить из виду важные логические выводы, сделанные на основе определенного набора данных.

Оглавление книги