Книга: Учебное пособие по курсу «Нейроинформатика»

Простой подбор

Простой подбор

Идея метода состоит в том, что бы начав с малого числа классов постепенно увеличивать его до тех пор, пока не будет получена «хорошая» классификация. Понятие «хорошая» классификация может быть формализовано по разному. При простом подборе классов как правило оперируют таким понятием, как часто воспроизводящийся класс. Проводится достаточно большая серия классификаций с различным начальным выбором классов. Определяются классы, которые возникают в различных классификациях. Считаются частоты появления таких классов. Критерием получения «истинного» числа классов может служить снижение числа часто повторяющихся классов. То есть при числе классов k число часто повторяющихся классов заметно меньше чем при числе классов k – 1 и k + 1. Начинать следует с двух классов.

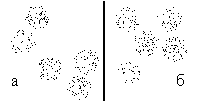
Рис. 10. Множества точек для классификации

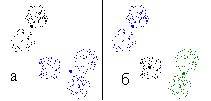
Рис. 11. Разбиение множества на два (а) и три (б) класса

Рассмотрим два примера. На рис. 10 приведены множества точек, которые будут разбиваться на классы. При каждом числе классов проводится 100 разбиений на классы. В качестве начальных значений ядер выбираются случайные точки.

Сначала рассмотрим множество точек, приведенное на рис. 10а. При классификациях на два класса во всех 100 случаях получаем классификацию, приведенную на рис. 11. Таким образом, получено устойчивое (абсолютно устойчивое) разбиение множества точек на два класса.

В принципе можно на этом остановиться. Однако возможно, что мы имеем дело с иерархической классификацией, то есть каждый (или один) из полученных на данном этапе классов может в дальнейшем разбиться на несколько классов. Для проверки этой гипотезы проведем классификацию на три класса. Во всех 100 случаях получаем одно и то же разбиение, приведенное на рис. 11б. Гипотеза об иерархической классификации получила подтверждение. Предпринимаем попытку дальнейшей детализации — строим разбиение на четыре класса. При этом возникают три различных разбиения, приведенных на рис. 12. При этом разбиение, приведенное на рис. 12в возникает всего два раза из 100. Разбиение, приведенное на рис. 12а — 51 раз, на рис. 12б — 47 раз. Если отбросить редкие классы, то получим набор из семи классов. Один из них воспроизводится 98 раз (красное множество на рис. 12а). Остальные шесть классов образуют две тройки. Каждая тройка состоит из двух классов и класса, являющегося их объединением. Из этого анализа напрашивается вывод о том, что число классов равно пяти. Проверяем это предположение.

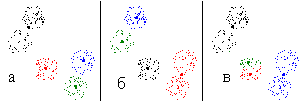
Рис. 12. Три варианта классификации на четыре класса

Результаты классификации на пять классов приведены на рис. 13. Выделенные на предыдущем этапе пять «маленьких» классов были воспроизведены 84, 67, 64, 68 и 69 раз. Два «больших» класса, выделенных на предыдущем этапе, были воспроизведены 24 и 30 раз. Остальные классы были получены не более чем 4 раза, а большинство по одному разу. Проверим классификацию на 6 классов. Малые классы были получены 75, 70, 53, 43, 44 раза. Один из больших классов — 16 раз. Из остальных классов один был воспроизведен 24 раза, второй — 19 раз. Все другие классы появлялись не более 10 раз. Всего получено 149 классов.

Рис. 13. Различные варианты классификации на пять классов

Таким образом, получена трехуровневая иерархическая классификация: Два класса первого уровня приведены на рис. 11а. Три класса второго уровня — на рис. 11б. Пять классов третьего уровня — на рис. 13а.

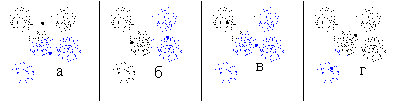
Рис. 14. Классификации на два класса

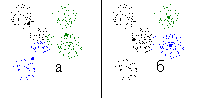
Рис. 15. Типы классификаций на три класса

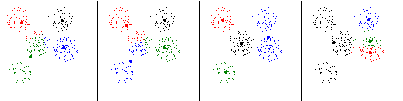
Рис. 16. Типичные классификации на четыре класса

Проведем туже процедуру для множества точек, приведенного на рис. 10б. При классификации на два класса получим четыре типичных варианта классификаций, приведенных на рис. 14. Всего получено 14 классов. Два класса были получены по 69 раз, два по 18 раз. Остальные не более 6 раз.

Проведем классификацию на три класса. Получим всего два типа классификаций, приведенных на рис. 15. Всего получено 12 классов. Одна тройка классов была воспроизведена 14 раз, вторая — 26 раз, третья — 27 и четвертая — 33 раза. После классификации на четыре класса получены четыре типичных классификации, приведенные на рис. 16. Всего получено 54 класса. Пять из них получены 36, 37, 36, 36 и 57 раз. Еще 4 класса получены 14 раз, два класса — 10 раз, остальные не более 6 раз. При классификации на пять классов получено семь типичных классификаций, приведенных на рис. 17. Всего было получено 49 классов. При этом пять классов были получены 91, 82, 87, 92 и 82 раза. Еще один класс — 8 раз. Остальные классы не более 3 раз. Увеличился разрыв между «редкими» и «частыми» классами. Сократилось число часто повторяющихся классов. Для контроля проведем классификацию на 6 классов. Всего получено 117 классов. Из них пять были получены 86, 81, 57, 76 и 69 раз. Все остальные классы были получены не более 9 раз.

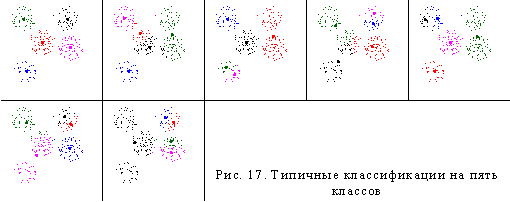
Таким образом, на основе классификаций на четыре, пять и шесть классов можно утверждать, что «реально» существует пять классов.

Оглавление книги