Книга: Учебное пособие по курсу «Нейроинформатика»

Прямой дубль второго рода

Прямой дубль второго рода

Перенумеруем входные сигналы из множества S₁={i₁,…,i_k}, k=|S₁|. Множество сигналов, являющееся прямым дублем второго рода для сигнала

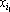
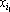
D_j=F({0},{1,…,M}{i_j}).

Полный прямой дубль второго рода получается объединением всех дублей для отдельных сигналов

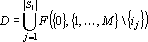
Множество повышенной надежности для прямого дубля второго рода можно записать в следующем виде:

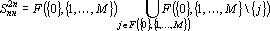
Заметим, что при построении прямого дубля второго рода не требовалось отсутствия в нем всех элементов множества S₁, как это было при построении прямого дубля первого рода. Такое снижение требований приводит к тому, что прямые дубли второго рода встречаются чаще, чем прямые дубли первого рода. Более того, прямой дубль первого рода очевидно является прямым дублем второго рода. Более точное соотношение между прямыми дублями первого и второго родов дает следующая теорема.

Теорема 2. Полный прямой дубль второго рода является прямым дублем первого рода тогда, и только тогда, когда

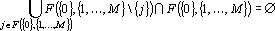
Доказательство. Построим сеть, состоящую из параллельно работающих сетей, T({0},{1,…,M}{i_j}), за которыми следует элемент, выдающтй на выход среднее арифметическое своих входов. Такая сеть очевидно будет решать задачу, а в силу соотношения (1) она будет сетью T({0},{1,…,M}{S₁}). Таким образом, если соотношение (1) верно, то прямой дубль второго рода является прямым дублем первого рода. Необходимость следует непосредственно из определения прямого дубля первого рода.

Оглавление книги