Книга: Учебное пособие по курсу «Нейроинформатика»

Построение оценки по интерпретатору

Построение оценки по интерпретатору

Если в качестве ответа нейронная сеть должна выдать число, то естественной оценкой является квадрат разности выданного сетью выходного сигнала и правильного ответа. Все остальные оценки для обучения сетей решению таких задач являются модификациями данной. Приведем пример такой модификации. Пусть при составлении задачника величина

, являющаяся ответом, измерялась с некоторой точностью e. Тогда нет смысла требовать от сети обучиться выдавать в качестве ответа именно величину
. Достаточно, если выданный сетью ответ попадет в интервал
. Оценка, удовлетворяющая этому требованию, имеет вид:

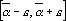
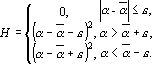
Эту оценку будем называть оценкой числа с допуском e.

Для задач классификации также можно пользоваться оценкой типа суммы квадратов отклонений выходных сигналов сети от требуемых ответов. Однако, эта оценка плоха тем, что, во-первых, требования при обучении сети не совпадают с требованиями интерпретатора, во-вторых, такая оценка не позволяет оценить уровень уверенности сети в выданном ответе. Достоинством такой оценки является ее универсальность. Опыт работы с нейронными сетями, накопленный красноярской группой НейроКомп, свидетельствует о том, что при использовании оценки, построенной по интерпретатору, в несколько раз возрастает скорость обучения.

Для оценок, построенных по интерпретатору потребуется следующая функция оценки

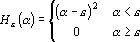
и ее производная

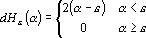
Рассмотрим построение оценок по интерпретатору для четырех рассмотренных в предыдущем разделе интерпретаторов ответа.

1. Кодирование номером канала. Знаковый интерпретатор. Пусть для рассматриваемого примера правильным ответом является k-ый класс. Тогда вектор выходных сигналов сети должен удовлетворять следующей системе неравенств:

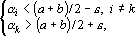
где e — уровень надежности.

Оценку, вычисляющую расстояние от точки a в пространстве выходных сигналов до множества точек, удовлетворяющих этой системе неравенств, можно записать в виде:

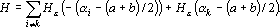
Производная оценки по i-му выходному сигналу равна

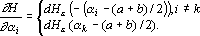
2. Кодирование номером канала. Максимальный интерпретатор. Пусть для рассматриваемого примера правильным ответом является k-ый класс. Тогда вектор выходных сигналов сети должен удовлетворять следующей системе неравенств: ?_k-e??_i при i?k. Оценкой решения сетью данного примера является расстояние от точки a в пространстве выходных сигналов до множества точек, удовлетворяющих этой системе неравенств. Для записи оценки, исключим из вектора выходных сигналов сигнал ?_k, а остальные сигналы отсортируем по убыванию. Обозначим величину ?_k-e через ?₀, а вектор отсортированных сигналов через ?₁??₂?…??N_-1. Система неравенств в этом случае приобретает вид ?₀??_i, при i>1. Множество точек удовлетворяющих этой системе неравенств обозначим через D. Очевидно, что если ?₀??₁, то точка b принадлежит множеству D. Если ?₀<?₁, то найдем проекцию точки b на гиперплоскость ?₀=?₁. Эта точка имеет координаты

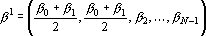
Если

, то точка ?? принадлежит множеству D. Если нет, то точку b нужно проектировать на гиперплоскость ?₀=?₁=?₂. Найдем эту точку. Ее координаты можно записать в следующем виде (b,b,b,?₃,…,?N_-1). Эта точка обладает тем свойством, что расстояние от нее до точки b минимально. Таким образом, для нахождения величины b достаточно взять производную от расстояния по b и приравнять ее к нулю:

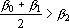
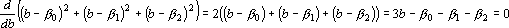
Из этого уравнения находим b и записываем координаты точки ??:

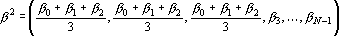
Эта процедура продолжается дальше, до тех пор, пока при некотором l не выполнится неравенство

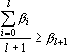
или пока l не окажется равной N–1. Оценкой является расстояние от точки b до точки

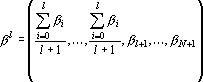
Она равна следующей величине

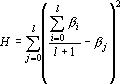
Производная оценки по выходному сигналу ?_m равна

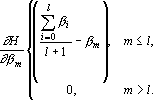
Для перехода к производным по исходным выходным сигналам ?_i необходимо обратить сделанные на первом этапе вычисления оценки преобразования.

3. Двоичный интерпретатор. Оценка для двоичного интерпретатора строится точно также как и для знакового интерпретатора при кодировании номером канала. Пусть правильным ответом является k-ый класс, тогда обозначим через K множество номеров сигналов, которым в двоичном представлении k соответствуют единицы. При уровне надежности оценка задается формулой:

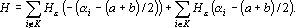
Производная оценки по i-му выходному сигналу равна:

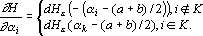
4. Порядковый интерпретатор. Для построения оценки по порядковому интерпретатору необходимо предварительно переставить компоненты вектора a в соответствии с подстановкой, кодирующей правильный ответ. Обозначим полученный в результате вектор через ??. Множество точек, удовлетворяющих условию задачи, описывается системой уравнений , где e — уровень надежности. Обозначим это множество через D. Оценка задается расстоянием от точки b до проекции этой точки на множество D. Опишем процедуру вычисления проекции.

1. Просмотрев координаты точки ??, отметим те номера координат, для которых нарушается неравенство ??_i+e???_i+1.

2. Множество отмеченных координат либо состоит из одной последовательности последовательных номеров i,i+1,…,i+l, или из нескольких таких последовательностей. Найдем точку ??, которая являлась бы проекцией точки ?? на гиперплоскость, определяемую уравнениями ??_i+e???_i+1, где i пробегает множество индексов отмеченных координат. Пусть множество отмеченных координат распадается на n последовательностей, каждая из которых имеет вид

, где m — номер последовательности. Тогда точка ?? имеет вид:

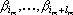
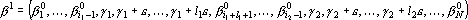
3. Точка ?? является проекцией, и следовательно, расстояние от ?? до ?? должно быть минимальным. Это расстояние равно

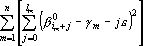
Для нахождения минимума этой функции необходимо приравнять к нулю ее производные по ?_m. Получаем систему уравнений

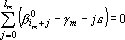
Решая ее, находим

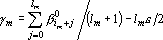
4. Если точка  удовлетворяет неравенствам, приведенным в первом пункте процедуры, то расстояние от нее до точки ?? является оценкой. В противном случае, повторяем первый шаг процедуры, используя точку ?? вместо ??; Объединяем полученный список отмеченных компонентов со списком, полученным при поиске предыдущей точки; находим точку ??, повторяя все шаги процедуры, начиная со второго.

Отметим, что в ходе процедуры число отмеченных последовательностей соседних индексов не возрастает. Некоторые последовательности могут сливаться, но новые возникать не могут. После нахождения проекции можно записать оценку:

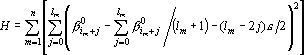
Обозначим через I_m m-ую последовательность соседних координат, выделенную при последнем исполнении первого шага процедуры вычисления оценки: I_m={i_m,i_m+1,…,i_m+l_m}. Тогда производную оценки по выходному сигналу ??_i можно записать в следующем виде:

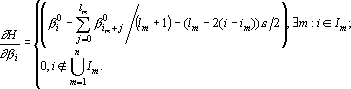
Таким образом, построение оценки по интерпретатору сводится к следующей процедуре.

1. Определяем множество допустимых точек, то есть таких точек в пространстве выходных сигналов, которые интерпретатор ответа будет интерпретировать как правильный ответ со стопроцентным уровнем уверенности.

2. Находим проекцию выданной сетью точки на это множество. Проекцией является ближайшая точка из множества.

3. Записываем оценку как расстояние от точки, выданной сетью, до ее проекции на множество допустимых точек. Оценка обучающего множества. Вес примера

В предыдущем разделе был рассмотрен ряд оценок, позволяющих оценить решение сетью конкретного примера. Однако, ситуация, когда сеть хотят обучить решению только одного примера, достаточно редка. Обычно сеть должна научиться решать все примеры обучающего множества. Ряд алгоритмов обучения, которые будут рассматриваться в главе «Учитель», требуют возможности обучать сеть решению всех примеров одновременно и, соответственно, оценивать решение сетью всех примеров обучающего множества. Как уже отмечалось, обучение нейронной сети — это процесс минимизации в пространстве обучаемых параметров функции оценки. Большинство алгоритмов обучения используют способность нейронных сетей быстро вычислять вектор градиента функции оценки по обучаемым параметрам. Обозначим оценку отдельного примера через H_i, а оценку всего обучающего множества через H_OM. Простейший способ получения H_OM из H_i — простая сумма. При этом вектор градиента вычисляется очень просто:

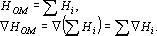
Таким образом, используя способность сети вычислять градиент функции оценки решения одного примера, можно получить градиент функции оценки всего обучающего множества.

Обучение по всему обучающему множеству позволяет задействовать дополнительные механизмы ускорения обучения. Большинство этих механизмов будет рассмотрено в главе «Учитель». В этом разделе будет рассмотрен только один из них — использование весов примеров. Использование весов примеров может быть вызвано одной из следующих причин.

Один из примеров плохо обучается.

Число примеров разных классов в обучающем множестве сильно отличаются друг от друга.

Примеры в обучающем множестве имеют различную достоверность.

Рассмотрим первую причину — пример плохо обучается. Под «плохо обучается» будем понимать медленное снижение оценки данного примера по отношению к снижению оценки по обучающему множеству. Для того чтобы ускорить обучение данного примера, ему можно приписать вес, больший, чем у остальных примеров. При этом оценка по обучающему множеству и ее градиент можно записать в следующем виде:

где w_i — вес i-го примера. Эту функцию оценки будем называть оценкой взвешенных примеров. При этом градиент, вычисленный по оценке решения сетью этого примера, войдет в суммарный градиент с большим весом, и, следовательно, сильнее повлияет на выбор направления обучения. Этот способ применим также и для коррекции проблем, связанных со второй причиной — разное число примеров разных классов. Однако в этом случае увеличиваются веса всем примерам того класса, в котором меньше примеров. Опыт показывает, что использование весов в таких ситуациях позволяет улучшить обобщающие способности сетей.

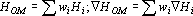
В случае различной достоверности примеров в обучающем множестве функция взвешенных примеров не применима. Действительно, если известно, что достоверность ответа в k-ом примере в два раза ниже, чем в l-ом, хотелось бы, чтобы обученная сеть выдавала для k-ого примера в два раза меньший уровень уверенности. Этого можно достичь, если при вычислении оценки k-ого примера будет использоваться в два раза меньший уровень надежности. Оценка обучающего множества в этом случае вычисляется по формуле без весов, а достоверность учитывается непосредственно при вычислении оценки по примеру. Такую оценку будем называть оценкой взвешенной достоверности.

Таким образом, каждый пример может иметь два веса: вес примера и достоверность примера. Кроме того, при решении задач классификации каждый класс может обладать собственным весом. Окончательно функцию оценки по обучающему множеству и ее градиент можно записать в следующем виде:

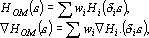
где w_i — вес примера, ?_i — его достоверность.