Книга: Introduction to Microprocessors and Microcontrollers

Floating point numbers

Eight-bit numbers are limited to a maximum value of 11111111₂ or 255₁₀. So, 0–255 means a total of 256 different numbers. Not very many. 32-bit numbers can manage about 4? billion. This is quite enough for everyday work, though Bill Gates’ bank manager may still find it limiting. The problem is that scientific studies involve extremely large numbers as found in astronomy and very small distances as in nuclear physics.

So how do we cater for these? We could wait around for a 128-bit microprocessor, and then wait for a 256-bit microprocessor and so on. No, really, the favorite option is to have a look at alternative ways of handling a wide range of numbers. Rather than write a number like 100 we could write it as 1?10?. Written this way it indicates that the number is 1 followed by two zeros and so a billion would be written as 1?10⁹. In a similar way, 0.001 is a 1 preceded by two zeros would be written as 1?10^–3 and a billionth, 0.000000001, would be 1?10^–9. The negative power of ten is one greater than the number of zeros. By using floating point numbers, we can easily go up to 1?10⁹⁹ or down to 1?10^–99 without greatly increasing the number of digits.

Fancy names

Normalizing

Changing a number from the everyday version like 275 to 2.75?10? is called normalizing the number. The first number always starts with a single digit between 1 and 9 followed by a power of ten. In binary we do the same thing except the decimal point is now called a binary point and the first number is always 1 followed by a power of two as necessary.

Three examples

1 Using the same figure of 275, this could be converted to 100010011 in binary. This number is normalized to 1.00010011?2⁸.

2 A number like 0.0001001₂ will have its binary point moved four places to the right to put the binary point just after the first figure 1 so the normalized number can be written as 1.001?2^–4.

3 The number 1.101² is already normalized so the binary point does not need to be moved so, in a formal way, it would be written as 1.101?2⁰.

Terminology

There are some more fancy names given to the parts of the number to make them really scary.

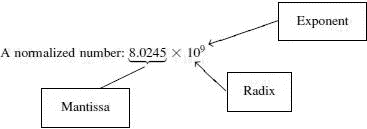
The exponent is the power of ten, in this example, 9. The mantissa, or magnitude, is the number, in this case 8.0245. The radix is the base of the number system being used, 2 for binary, 16 for hex, 10 for decimal.

Storing floating point numbers

In a microprocessor, the floating point is a binary number. Now, in the case of a binary number, the mantissa always starts with 1 followed by the binary point. For example, a five digit binary mantissa would be between 1.0000 and 1.1111.

Since all mantissas in a binary system start with the number 1 and the binary point, we can save storage space by missing them out and just assuming their presence. The range above would now be stored as 0000 to 1111.

It is usual to use a 32-bit storage area for a floating point number. How these 32 bits are organized is not standardized so be careful to check before making any assumptions. Within those 32 bits, we have to include the exponent and the mantissa which can both be positive or negative. One of the more popular methods is outlined below.

Bit 0 is used to hold the sign-bit for the mantissa using the normal convention of 0 = positive and 1 = negative.

Bits 1–23 hold the mantissa in normal binary.

Bits 24–31 hold the exponent. The eight digits are used to represent numbers from –127 to +128 using either two’s complement numbers or excess-127 notation.

We have already met two’s complement numbers earlier in this chapter so we will look at excess-127 notation now.

Excess-127 notation

This is very simple, despite its impressive name. To find the exponent just add 127 to its value then convert the result to binary. This addition will ensure that all exponents have values between 0 and 255, i.e. all positive values.

Example

If the exponent is –35 then we add 127 to give the result 92, which we can then convert to binary (01011100).

When the value is to be taken out of storage and converted back to a binary number, the above process is reversed by subtracting the 127 from the exponent.

Оглавление книги