Книга: Introduction to Microprocessors and Microcontrollers

Subtraction

Here is a question to think about: What number could we add to 50 to give an answer of 27? In mathematical terms this would be written as 50+x=27.

What number could x represent? Surely, anything we add to 50 must make the number larger unless it is a negative number like –23:

50 + (–23) = 27

The amazing thing is that there is a number that can have the same effect as a negative number, even though it has no minus sign in front of it. It is called a ‘two’s complement’ number.

Our sum now becomes:

50 + (the two’s complement of 23) = 27

This magic number is the two’s complement of 23 and finding it is very simple.

How to find the two’s complement of any binary number

All we have to do is to take the number we want to subtract (in its binary form) and invert each bit so every one becomes a zero and each zero becomes a one. Note: technically the result of this inversion is called the ‘one’s complement’ of 23. The mechanics of doing it will be discussed in the next chapter but it is very simple and the facility is built into all microprocessors at virtually zero cost.

Converting the 23 into a binary number gives the result of 00010111₂ (using eight bits). Then invert each bit to give the number 11101000₂ then add 1. The resulting number is then referred to as the ‘two’s complement’ of 23.

Introduction to Microprocessors and Microcontrollers In this example, we used 8-bit numbers but the arithmetic would be exactly the same with 16 bits or indeed 32 or 64 bits or any other number.

Doing the sum

We now simply add the 50 and the two’s complement of 23:

50 + (the two’s complement of 23) = 27

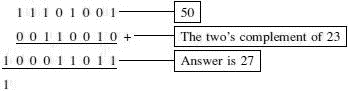
The answer is 100011011.

Count the bits. There are nine! We have had a carry in the last column that has created a ninth column. Inside the microprocessor, there is only space for eight bits so the ninth one is not used. If we were to ask the microprocessor for the answer to this addition, it would only give us the 8-bit answer: 00011011₂ or in denary, 27. We’ve done it! We’ve got the right answer!

It was quite a struggle so let’s make a quick summary of what we did.

1 Convert both numbers to binary.

2 Find the two’s complement of the number you are taking away.

3 Add the two numbers.

4 Delete the msb of the answer.

Done.

A few reminders

1 Only find the two’s complement of the number you are taking away – NOT both numbers.

2 If you have done the arithmetic correctly, the answer will always have an extra column to be deleted.

3 If the numbers do not have the same number of bits, add leading zeros as necessary as a first job. Don’t leave until later. Both of the numbers must have the same number of bits. They can be 8-bit numbers as we used, or 16, or 32 or anything else so long as they are equal.

Оглавление книги