Книга: Программирование игр и головоломок

5. Стратегия без игры (выигрывающие стратегии)

5. Стратегия без игры (выигрывающие стратегии)

Я объединил в этой главе несколько игр, которые можно найти на рынке и для которых существует стратегия решения. Как только она становится известной, игра теряет всякий интерес. Единственное связанное с такими играми удовольствие — обнаружить, как с ними покончить. Поэтому напишите программу — это наилучший способ сформулировать выигрышную стратегию, а затем забудьте игру, она вам больше ничего не принесет. И тем хуже, если продавцы этих игр не согласятся со мной… Некоторые из этих игр являются классическими среди информатиков. Я попытался их немного подновить. Многие стратегии могут быть элегантно запрограммированы с помощью рекурсивных процедур, но на языке Бейсик это невозможно. Всегда наступает день, когда фанатики этого языка, такого удобного для первых шагов, начинают понимать его ограниченность… Рекурсивность допустима в языках LSE и Паскаль.

? Игра 27. Бездельник.

Эта игра на рынке есть. Она имеет вид дощечки, в которую продето n гвоздей, скользящих через соответствующее отверстие, причем концы гвоздей расплющены и в каждом просверлено отверстие, в которое продето кольцо. Вы безусловно можете изготовить все это сами, используя достаточно толстые гвозди (диаметром порядка четырех миллиметров). Пропустите гвоздь в отверстие в 5 миллиметров в дощечке, а затем расплющите острие молотком. Просверлите головку наконечника, образовавшуюся у конца гвоздя, и вставьте туда кольцо для ключей. Каждое кольцо должно проходить вокруг предыдущего гвоздя. Трудность игры зависит от n. Для n = 6 она довольно быстро приходит к концу. Для n = 8 она требуем долгих минут. Она почти невыполнима, если n больше восьми.

Через кольца проходит челнок, длинный замкнутый контур, представленный на рисунке. Дело в том, чтобы его вынуть и, таким образом, освободить от колец (рис. 17).

Первое, что нужно сделать — это научиться, как пропускать одно кольцо через челнок, или как его оттуда вынуть. Несколько манипуляций — и вы быстро убеждаетесь, что в какой стадии ни была бы игра, всегда можно надеть или снять первое кольцо, которое свободно (не проходит вокруг какого-либо гвоздя). Можно также освободить кольцо, которое следует за первым занятым кольцом (если оно проходит вокруг челнока), или одеть его на челнок, если оно не одето. Таким образом, игру «бездельник» можно заменить равносильной игрой, которую легче представить на компьютере.

Эта игра ведется на таблице, разделенной на несколько полей (8 полей на рисунке). В начальном состоянии каждое поле покрыто шашкой. Поля размечены цифрами. Играть на данном поле — значит, поставить туда шашку, если поле пусто, и удалить шашку, стоящую на этом поле — в противоположном случае. Правила игры следующие:

— можно всегда играть на первом поле,

— можно играть на поле, которое следует за первым занятым полем.

Есть две возможных игры:

НАДЕВАТЬ: игровое поле вначале пусто. Заполнить все поля.

СНИМАТЬ: игровое поле вначале наполнено шашками на каждой клетке. Нужно все убрать,

Эта задача имеет очень элегантное рекурсивное решение. Но если вы немного подумаете, то вы сможете также найти очень простое итеративное решение, причем игра НАДЕВАТЬ оказывается более простой, чем игра СНИМАТЬ.

Вот другая интерпретация этой игры — для тех, кто любит арифметику. Вы можете считать, что каждое поле может принимать два состояния (свободное и занятое), что эквивалентно двоичным числам — например, 0 для свободного и 1 для занятого полей. Тогда каждая конфигурация является представлением целого числа по основанию 2. Таким образом, рис. 18 представляет целое число 11111111 в качестве начального состояния и 01011011 в качестве промежуточного состояния. Ниже нам будет удобно читать эти слова в обратном порядке, так что в этих новых обозначениях промежуточное состояние соответствует двоичному числу 11011010.

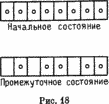
Ясно, что эта игра порождает последовательность чисел (в приведенном выше примере число равно 218 в десятичной записи). При переходе от одного числа к следующему меняется лишь одна двоичная цифра. Можете ли вы сказать, какая последовательность порождается таким образом в каждой из игр?

?* Игра 28. Зануда,

Эта игра называется также «игра в лягушек». У нее была версия, использованная в материалах лицеев, но в ней было не все, что я вам сейчас предлагаю. Игровое поле снова имеет вид прямоугольной площадки, разделенной на поля. Число полей должно быть нечетным (9 на рис. 19). Поля слева покрыты шашками некоторого цвета (я представил их ноликами), поля справа — шашками другого цвета (здесь — крестиками). Среднее поле свободно. Крестики могут передвигаться только влево, нолики — только вправо. Шашка может быть либо подвинута на один шаг, если следующее поле в направлении ее перемещения свободно, либо перепрыгнуть через шашку другого рода, если следующее за ней поле свободно. Рисунок 20 иллюстрирует два возможных хода в партии с начальным положением на рис. 19.

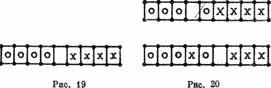
Цель игры состоит в том, чтобы привести все X влево, а все 0 вправо, так что конечное состояние должно быть похоже на начальное, и шашки должны поменяться местами (крестики справа, нолики слева).

Программа, которую вы должны составить, должна описывать последовательность перемещений шашек для произвольного (но, конечно, нечетного) числа полей. Вы можете получить решение в виде пары рекурсивных процедур или в виде одной итеративной программы. Как только вы найдёте стратегию, зануда не будет больше представлять никакого интереса. Как это случилось с теми, с кем я занимался на Митра 15, в лицее, требуя, чтобы игрок сидел за своей клавиатурой и переставлял шашки. Но если не знать стратегии и действовать случайным образом, то выиграть нельзя вследствие теоремы Дюнойе: «Если какой-то выбор вы делаете случайным образом, то вы всегда проигрываете». Это нам постоянно повторял наш учитель математики, когда я был в подготовительном классе Политехнической школы. Мы придумали следствие: поскольку мы всегда проигрываем при случайном выборе, то достаточно после этого выбора выбрать другую сторону альтернативы. Но это дает выход из парадокса Дюнойе (я совершенно не знаю, кто такой Дюнойе. Это — существенный момент истории науки, который следовало бы прояснить. Всегда цитируют Мэрфи и его знаменитые законы: если в некотором опыте что-то может разладиться, то можно быть уверенным, что это обязательно произойдет. Если, кроме того, при этом в комнате есть посторонний наблюдатель, то он прибавит «ну, я же так и говорил…». Дюнойе — предшественник Мэрфи), Вот в чем парадокс. Есть альтернатива. Вы выбрали случайным образом и обманулись. Следовательно, если вы взяли другую сторону альтернативы, то вы оказались правы. Но это — тоже случайный выбор, поэтому вы опять обманулись…

?* Игра 29. Б — А — БА.

Эта игра вовсе не потому самая простая среди всех игр этого сорта, что она называется б—а—ба. Согласно [BAL], она имеет японское происхождение. Ее можно сформулировать следующим образом. Игра разыгрывается на площадке, разделенной на клетки, на этот раз в четном числе. Есть шашки двух сортов, скажем, крестики и нолики — как в «зануде». В начале игры два левых поля свободны, остальные заняты поочередно 0 и X, как указано на рис. 21. При каждом ходе вы можете переместить пару смежных шашек, перенося ее на пару смежных свободных клеток. Вы выиграете, когда все X будут вместе стоять на левых полях, затем будут нолики, а два правых поля останутся свободными.

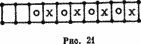
Можно также представить это другим способом. Свободные поля представляются точками (рис. 22), остальные заняты буквами а и б (вот вам и б — а — ба).

Пара шашек, которая переносится при данном ходе, абсолютно произвольна: две одинаковых буквы, две разных буквы, все равно в каком порядке…

Начните с решения задачи для 8 букв и 10 полей, как на рисунке. Это очень просто и у вас нет необходимости » компьютере. Попробуйте затем решить ее для бо?льшего числа полей.

Честно говоря, я соответствующую программу не написал, потому что ее использование на компьютере меня ничему новому не научило бы. То, что здесь приведено, подходит программисту, который на что-то рассчитывает. Если у вас есть склонность к программированию, то вы найдете способ решить задачу для всех случаев,

* Игра 30. Отшельник.

Может быть, мне и не следовало бы помещать «Отшельника» в эту главу, Классификация игр полностью основана на оттенках и на индивидуальных оценках. Я провел немало времени в забавах с «Отшельником», но все же верно, что едва только удается обнаружить хорошую стратегию, как интерес уменьшается. Возможность его программирования связана с улучшениями. «Отшельник» разыгрывается на площадке с проделанными в ней отверстиями, в которых могут быть размещены шашки. Но можно также использовать доску, на которой нарисованы поля, а можно также все это очень хорошо нарисовать на земле и использовать камешки в качестве шашек — точно так же, как я рассказывал при игре в лис и кур. Впрочем, может оказаться, что «отшельник» был изобретен каким-нибудь знатным французом, заключенным в Бастилию, который модифицировал игру в лиси кур.

Рисунок 23 представляет одно из состояний игры в «Отшельника». Свободные места представлены точками, шашки — знаком ?. Как показывает название, это — игра для одного-единственного лица. При каждом ходе нужно съесть шашку, заставляя перепрыгнуть через нее другую шашку так, чтобы попасть на свободное поле — либо горизонтально, либо вертикально. Так, на рис. 23 имеется 4 возможных хода:

— шашка, лежащая на пересечении планок креста, может ваять шашку, расположенную непосредственно над ней, и попасть в середину верхней строки (шашка, через которую перепрыгнули, а именно, расположенная в вершине креста, удаляется из игры);

— та же шашка может взять шашку слева;

— или шашку справа;

— наконец, шашка в центре игрового поля может взять шашку под ней, расположенную в низу креста.

Цель игры состоит в том, чтобы удалить все шашки, кроме одной. Число необходимых для этого ходов легко подсчитать: поскольку при каждом ходе берется одна шашка, то число ходов равно числу подлежащих удалению шашек. В случае креста на рис. 23 вам осталось сделать до конца еще 5 ходов.

Составьте программу для отшельника. Вы даете компьютеру начальную конфигурацию, например крест на рис. 23. Он сообщает вам ходы, которые приводят к решению.

Другие конфигурации приведены на рис. 24.

В своей наиболее общей форме эта игра начинается с игрового доля, полностью покрытого шашками, кроме единственного остающегося свободным поля. Попробуйте заставить вашу программу работать и в этом случае. У вас появится новая трудность, связанная с симметрией игры: есть много решений, эквивалентных с точностью до симметрии.

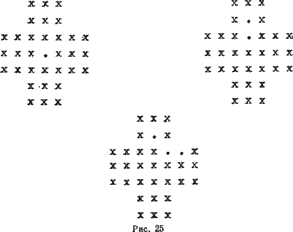
На рис. 25 сначала изображена исходная конфигурация. Есть 4 различных хода — шашка из перекладины креста прыгает в центр игрового поля. Эти 4 хода начинают 4 решения, эквивалентных с точностью до поворота на прямые углы. После этого остаются еще две возможности эквивалентности с помощью симметрии относительно вертикальной оси игры. Нижняя конфигурация показывает результат одного из этих ходов.

В позиции, к которой мы пришли, никакой симметрии уже нет. Ее-то и возьмите как исходную.

Ваша программа дает только одно решение или все возможные решения?

Очень мало говорят о печальном конце Паскаля Младшего. Его бывшие коллеги знали, что у него возникли проблемы, заставившие поместить его в психиатрический госпиталь. Теперь когда он умер, я могу опубликовать письмо, которое он мне послал в свое время; оно уже больше не может причинить ему вреда…

«Господин профессор,

Я не знаю, помните ли вы меня: я был вашим учеником в Институте программирования. Конечно, у вас их столько было… После того, как я окончил институт, я поступил на работу программистом-аналитиком в бюро обслуживания. Я был на очень хорошем счету. Я следовал вашим урокам: использовал программирование «сверху-вниз», я выводил свои циклы в программах, используя пост- и предусловия и инварианты. Мои программы работали верно с первого запуска, с точностью до опечаток. Короче, по прошествии нескольких лет я сказал себе, что у меня будет более интересная работа, если я буду вести ее на свой собственный счет. Поэтому я нее подготовил, нашел помещение. Я подал в отставку и взял все отложенные отгулы, на которые я имел право. Будучи холостым, я, вообще говоря, брал очень мало выходных дней, настолько меня захватывала моя работа. Но, собираясь испытать счастья в большом деле и становясь своим собственным работодателем, я хотел получить настоящий отдых.

Право, я не знаю, как это меня по рекламному объявлению занесло в бюро путешествий «Посетите таинственную Индию». И вот я отправился с тремя десятками других в организованное путешествие. Конечно, я должен был задуматься раньше, то ли я выбрал, что мне нужно. Оказалось, что я с трудом переношу беспрерывную болтовню то одних, то других; это мешало мне думать о чем-нибудь своем. Мне пришлось примириться с тем, что мне придется думать о чем-то еще, кроме написания какой-то упирающейся программы! Детали этого путешествия несущественны вплоть до дня, когда нас привезли в монастырь в предгорьях Гималаев.

Монах, который нас принял, говорил на отличном французском. Сообщение, которое он сделал о монастыре, свидетельствовало о свободном владении нашим языком. Это должно было показаться мне подозрительным. Он ввел нас в помещение и, с того момента как я вошел, я смог только выдавить «ох» изумления: мы увидели монаха, который занимался знаменитейшей игрой в Ханойские башни. Диски были, очевидно, из золота, и я сразу угадал, даже не считая, их ровно 50. Монах объяснял игру посетителям:

«Как вы видите, игра состоит из круглой подставки с тремя стержнями. На стержни нанизаны диски различных диаметров. (Рис. 26 представляет конфигурацию игры с семью дисками.) На каждом стержне диски сложены, в стопку по возрастанию диаметра: никогда ни один диск не кладется на другой диск меньшего диаметра, В начале игры, это было много лет назад, даже много веков, все пятьдесят дисков находились на первом стержне. Монах перекладывает эти диски один за другим, следуя методу, который мы тщательно продумали. Когда все диски соберутся снова на одном стержне, отличающемся от исходного, игра кончится. Великий труд, который боги наложили на людей, будет завершен, и сможет наступить конец света…»

Я решил насмешливо добавить вполголоса: ну, это еще не завтра… Это стоило мне разгневанного взгляда гида, который продолжал:

«Как только что заметил один из вас, это занятие потребует еще многих столетий, несмотря на большую сноровку монахов, которые перекладывают каждый диск приблизительно за одну секунду». Я снова продемонстрировал свое раздражение, Разумеется, я предполагал, что из-за меня посещение будет сокращено. Но не для того же я сюда приехал, чтобы надо мной, как и над остальными путешественниками, насмехались? Мы хорошо знаем, что игра в ханойские башни была изобретена в конце прошлого века преподавателем математики в лицее Сент- Луи по имени Люка, который под этим соусом ее и пустил в свет, окружив легендой, согласно которой монахи где-то в Индии суетятся вокруг игры в 50 дисков, по окончании которой наступит конец света. Эта легенда делала естественной задачу о подсчете числа ходов, Необходимых для завершения игры. Что же касается того, что каждый диск перекладывается за секунду, то это элементарно, и мы знаем итеративную стратегию, которая позволяет нам просто играть, ни о чем не думая — вы ее нам сами давали в вашем курсе в институте…

Когда мы покидали монастырь, наш гид подошел ко мне и спросил меня, не хочу ли я оказать его настоятелю большую честь своим посещением. Обсуждение с руководителем группы. Назавтра мы не должны были уезжать рано, и поэтому я принял приглашение снова прийти туда до нашего отъезда. Настоятель принял меня очень любезно и предвосхитил мои упреки: «Несомненно, вы уже знакомы с башнями Брахмы. Мы знаем, что они были введены во Франции много лет назад М. Люка. Он никогда не говорил, что он сам придумал эту игру. Совсем наоборот, он очень добросовестно изложил то, что мы делаем. И разве мы виноваты в том, что вы вбили себе в голову, что с его стороны это была чистейшая уловка, чтобы придать больший блеск своему мнимому открытию? А это была и в самом деле чистейшая уловка, потому что ему приписали создание этой игры, в то время как он всего лишь пересказал то, что ему описал один путешественник… Нас тревожит то невероятное время, которое нужно для окончания игры. Мы очень терпеливы, однако мы ищем, как двигаться быстрее. Один наш посетитель, приехавший из американского университета, предложил нам сконструировать робота-манипулятора, управляемого компьютером. Мы со своей стороны финансировали это исследование. Но робот не мог двигаться быстрее, чем наши монахи, натренированные до совершенства и действовавшие безошибочно». Когда же я высказал замечание, что при таком решении проблемы игру будут вести уже не люди, а машина, настоятель решительно возразил мне, сказав: «Мы прекрасно пользуемся молитвенными мельницами. Во всяком случае, машина делается людьми и управляется программой, написанной людьми…»

Он также сказал мне, каким образом это исследование к тому же открывает новые перспективы. Были времена, когда монахи пытались присоединить к игре четвертый стержень. Правила оставались такими же: перемещать за один раз не более одного диска и никогда не класть диск на другой диск меньшего диаметра. Конечно, манипуляция игрой с 50 дисками до сих пор не удалась. Они вывели, что при этом требуется гораздо меньше ходов, но стратегия манипулирования становится много сложнее. Монахи терялись, часто оказывалось, что они ошибаются, они снова попадали в уже пройденные конфигурации, так что не было никакой уверенности в том, что удастся дойти до конца, если постоянно приходится начинать сначала… «Не могли бы вы взяться за решение проблемы башен Брамы с четырьмя стержнями, составить программу для соответствующего компьютера и использовать его для управления роботом, манипулирующим игрой? Ведь даже если каждый ход отнимет много секунд, конец должен будет наступить намного быстрее. А нам, таким образом, выпадет величайшая радость — стать теми, кто выполнил волю богов. Мы увидим, что мир достиг своего конца, и вступим в счастье, которое никогда не кончится…»

Это дело показалось мне выполнимым, Договорились, что я реализую информативную систему и передам ее им. Настоятель вручил мне в качестве оплаты авансом игру, сделанную из серебра. Это было настоящее богатство. Ну, как тут устоять?

Вернувшись во Францию, я взялся за работу. Больших трудностей она не представляла. Вначале я составил рекурсивную процедуру для решения игры с четырьмя стержнями. Поскольку я искал оптимальную стратегию, я сделал по ней итеративную версию. Для этой маленькой программы был достаточен микрокомпьютер. Я использовал ручной манипулятор, оснащенной электромагнитом в форме кольца. Я работал с деревянной игрой, каждый диск которой был снабжен маленьким кольцом из мягкого железа, позволявшим ручному манипулятору брать его, и притом не возникало необходимости чрезвычайно точно этот диск устанавливать.

И я был всем очень доволен, пока не понял внезапно, что я без раздумий бросился в ужасное предприятие. А что, если монахи говорили правду? Какую пользу мне принесет обладание богатством (ибо они должны были заплатить мне еще, если программа будет работать правильно), если вскоре наступит конец света? Безусловно, будучи убежденным рационалистом, я не очень-то всерьез принимал их истории. Но, в конце концов, это — новая форма пари Паскаля[15]. Даже если шанс, что все это верно, бесконечно мал, я не испытывал ни малейшего желания ускорять конец света. Но прошлое вернуть нельзя, и их плату я уже получил,

Мне пришла в голову поистине дьявольская мысль: эти прекрасные монахи желали конца света, чтобы как можно скорее достичь вечного счастья, вот уж я его им обеспечу, В корпус компьютера я добавил выдвижной ящик, который окрестил «концом света». В нем были под видом блока питания толстые цилиндры, на корпусах которых была маркировка конденсаторов, но в которых находились пластиковые бомбы. Маленькое изменение программы должно было вызвать взрыв сразу же после того, как наименьший диск покидал свой стержень и перед тем, как он достигал места своего назначения. Таким образом, игра никогда не должна была кончиться. Что до монахов, то они будут с восторгом представлять себе конец света в тот момент, когда завершится игра. В тот момент чудовищность моего поступка меня не шокировала. Наоборот, я был в восторге: монахи будут счастливы, а я уберегу весь мир от конца. Я дошел до того, что смотрел на себя как на благодетеля человечества. Конечно, я брал на себя риск. Программу, без сомнения, нужно было испытать. Но, как я вам уже говорил, я прошел хорошую школу — Вашу школу — и я программировал правильно.

Когда все было закончено, я отправился вручить свое произведение сияющим монахам. Она была испытана на игре в 20 дисков. Затем аппарат был пущен в работу для игры с 50 дисками и 4 стержнями. Тут я попросил у монахов разрешения удалиться: ведь мне хотелось бы привести свои дела в порядок в то небольшое время, которое осталось нам жить, что они очень хорошо понимали. Я вое Братался с полными пригоршнями золота.

Через некоторое время сообщили, что ужасный взрыв неизвестного происхождения разрушил монастырь в Индии. В живых не осталось никого. Моя программа была правильной…

Уже позже меня стали одолевать сомнения. Не были ли монахи правы? Не я ли тот, кто помешал воле богов? Не воспрепятствовал ли я выполнению работы, которая была доверена людям? Не должен ли я сконструировать игру в 50 дисков, и не следует ли ее разыграть, чтобы искупить свою вину?

С этих пор я живу в ужасе. Если я ничего не делаю, я несу на себе груз того, что я препятствую воле богов. Если я сделаю игру, что для меня не составляет никакого труда, то именно я и приведу мир к гибели… Я никому не могу довериться. Я умоляю вас, помогите мне…»

Я не стал вмешиваться. Душа Паскаля Младшего не могла сопротивляться этому удару. Он впал в безумие и немного спустя умер…

Игра 31. Рекурсивная форма.

Письмо Паскаля Младшего ставит много задач по программированию. Я не осмеливаюсь предложить вам написать рекурсивную процедуру, которая перечисляет последовательность движений дисков в игре с тремя стержнями, помеченными номерами 0, 1 и 2 (например, в форме последовательности строк ДИСК 2 ИДЕТ С 1 НА 0, дающих номер перемещаемого диска, если наименьший диск имеет номер 1, номер стержня, с которого диск снимается, и номер стержня, на котором этот диск оказывается).

Тем не менее эта процедура была бы для вас очень полезна как для наблюдения за перемещениями в течение партии, так и для изучения свойств игры.

Можете ли вы вычислить число f(n) ходов, необходимое для проведения партии в игре с n дисками? Сколько веков потребуется для проведения игры в 50 дисков, если каждый ход делается за секунду?

Я использовал игру из дерева, в которой диски были обтесаны из двух разных пород дерева, поочередно светлых и темных. Проводя игру, можно убедиться, что два диска одного и того же цвета никогда не оказываются друг на друге. Сумеете ли вы показать это с помощью рассуждения, основанного на рекурсивной процедуре? Заметьте, что это сводится к вопросу четности. Если диски занумерованы так, как это было описано выше, то диски с номерами одинаковой четности никогда не попадают друг на друга.

* Игра 32. Рисунок игры.

Напишите простую рекурсивную процедуру, наиболее образно дающую возможность увидеть движение дисков. Очень общий способ состоит в том, чтобы изобразить три стержня в виде трех строк, на которых последовательно поставлены номера дисков. Таким образом, рис. 27 представляет начальное состояние и промежуточное состояние игры с 5 дисками.

Внимание: ваша программа работает слишком быстро, и вы не видите перемещений. Вставьте цикл ожидания, чтобы замедлить игру…

Более хитрый способ представляет стержни вертикально либо как последовательность номеров, либо — что еще лучше — если у вас есть графическая система, стилизованным образом, как на рис. 26. Это труднее…

? Игра 33. Итеративная стратегия.

Таких стратегий много. Сумеете ли вы предложить такую, которая позволила бы играть по ходу в. секунду, как у монахов…

??? Игра 34. Игра с 4 стержнями.

Составьте рекурсивную программу для игры с 4 стержнями, не занимаясь представлением дисков на экране каким-либо хитрым образом. Вам и бее этого будет достаточно работы. Даже если ваш компьютер не предоставляет вам возможности вычислять рекурсивные процедуры, это поможет вам ясно увидеть задачу и найти стратегию.

Найдите способ действовать, минимизируя число ходов, и найдите их необходимое число для малых значений n. Из письма Паскаля Младшего неясно, сколько времени нужно — если каждый ход совершается за секунду — для завершения игры с 4 стержнями и 50 дисками. Вычислите его.

??** Игра 35. Составьте итеративную программу для игры с 4 стержнями.

Если теперь добавить пятый стержень, то нужно все начинать сначала, или результаты, полученные для 4 стержней, допускают немедленную экстраполяцию на случай 5 стержней?

??? Игра 36. Спички Бергсона.

Эта игра была предложена выше (игра 23). Тогда требовалось только дать компьютеру указание, что он должен будет сделать, чтобы выиграть наверняка, если исходить из 50 спичек. Теперь нужно заглянуть глубже и изучить выигрывающую стратегию в полной общности.

Как и во многих играх, есть ситуации, которые позволяют игроку выиграть наверняка (если он их знает), и другие ситуации, исходя из которых выиграть невозможно. Пусть П обозначает ситуацию, благоприятную первому игроку (или предыдущему. П — это первая буква слова «позитивный», как это заметил Роуэ Болл [BAL]). Эта ситуация хороша для меня, если это такая ситуация, которой я достигаю после своего хода. Ситуация Н благоприятна второму, «новому», игроку (неблагоприятна первому, негативна). Она хороша для меня, если это — та ситуация, которую я застаю в момент своей игры. Вся моя стратегия есть переход от ситуации Н в ситуацию П.

Это все работает, если, исходя из ситуации Н, я всегда могу достичь ситуации П с помощью разрешенного хода, и если, с другой стороны, налицо ситуация П, то я не могу достичь никакой ситуации П с помощью дозволенного мне хода. Итак:

— из ситуации Н всегда можно достичь ситуации П,

— из ситуации П можно достичь только ситуаций Н,

— выигрывающая ситуация есть ситуация П.

Игра происходит переходами между ситуациями Н и П. Победитель определяется природой — принадлежностью классу Н или П — начальной ситуации и, таким образом, определяется тем, кто начинает.

В игре в спички Бергсона ситуация характеризуется двумя целыми числами p, q:

p — число спичек, оставшихся в куче;

q — число спичек, взятых на предыдущем шаге. Тогда можно взять от 1 до 2q спичек.

Ситуация 0, q — выигрывающая для любого q.

Ситуации 1, q и 2, q суть ситуации Н. Исходя из них,; можно взять последнюю спичку. Ситуация 3, 1 есть П: исходя из нее, нельзя получить ничего, кроме 2, 1 и 1, 2, и обе эти ситуации относятся к классу Н.

Составьте программу, перечисляющую положения П вплоть до некоторого уровня.

Понаблюдайте за результатами. Попытайтесь угнать их свойства и, если вам хватит смелости, проверить их.

Вы наверняка знаете числа Фибоначчи: они определяются рекуррентным соотношением

f(n) = f(n ? 1) + f(n ? 2)

и единичными значениями двух первых чисел. Какой черт их сюда занес…

Оглавление книги