Книга: Программирование игр и головоломок
4. Игры со стратегией
4. Игры со стратегией
В этом разделе мы предлагаем программировать игры, главная трудность которых заключается в том, чтобы дать компьютеру хорошую стратегию. Разделение па игры со стратегией и без нее до некоторой степени произвольно. Уже по поводу случайных чисел мы предлагали игру со стратегией (игра 2). Конечно, совершенно необходимо, чтобы вы могли хоть немного развлечься… Некоторые из игр, с которыми вы познакомитесь, требуют не намного больше размышлений, чем игра в лис и кур. На самом деле это во многом зависит от особенностей вашего ума: стратегия, очевидная для одного, является головоломкой для другого.
Можно также упрекнуть некоторые игры в том, что они теряют всякую привлекательность, поскольку компьютер располагает выигрывающей стратегией. Если партнер компьютера не знает этой стратегии, то он проигрывает все партии. Если же он ее знает, то тот, кто делает выигрывающий начальный ход, неминуемо становится победителем.
Наконец, некоторые игры настолько распространены, что я постеснялся их здесь предлагать: такова, например, игра Отелло. Не пытайтесь браться за шашки или шахматы. Слишком трудно!
В этом разделе вам предстоит встретиться с двумя трудностями:
— найти стратегию для компьютера;
— запрограммировать ее.
Именно потому, что есть так много опубликованных плохих программ, я, не ссылаясь на эти публикации, добавил игру Нима, Сочувствую всем тем, кто может оказаться обиженным. Но тот, кто публикует программы, всегда рискует. Таковы правила этой игры.
Игра 16. Чтобы войти в курс дела,
Это — крайне простая игра, которую Роуз-Бол [BAL] относит к средневековым играм, поскольку ей действительно более 500 лет.
Вы выкладываете на стол 50 спичек. Каждый игрок по очереди вынимает спички из кучи, по меньшей мера 1 и не более 6. Кто берет последнюю спичку, выигрывает.
Вы можете реализовать ее, заставляя компьютер сообщать число оставшихся спичек, Когда очередь хода за компьютером, он делает ход настолько быстро, что игрок не успевает увидеть происходящего. Включите в вашу программу «цикл ожидания», чтобы замедлить игру компьютера (цикл от 1 до нескольких тысяч, в котором ничего не происходит:
ДЛЯ i = 1 ДО 2000 ВЫПОЛНЯТЬ ВЕРНУТЬСЯ)
Вы можете изменить игру, взяв в качестве допускающих изменение данных — начальное число спичек и максимальное число спичек( которое можно вытащить на каждом ходе.
? Игра 17. Игра дат.
Эта игра предложена Берлокеном [BER]. Номер года в ней не очень существен, но предполагается, что год не високосный: в феврале 28 дней. Первый игрок сообщает какую-нибудь дату января. Каждый игрок на своем ходе называет более позднюю дату, увеличивая либо календарную дату в месяце, либо месяц, но не то и другое сразу. Если, например, начальной датой было 8 января, то можно перейти к 8 марта или к 12 января. Можно увеличить меньше: 9 января или 8 февраля; можно перейти сразу к 8 декабря или 31 января. Внимание: если вы переходите к 31 января, то ваш противник сможет в дальнейшем менять только месяцы, и притом лишь месяцы с 31 днем.
Первый, кто доберется до 31 декабря, выигрывает.
У вас не должно возникнуть никаких затруднений ни в определении стратегии, ни в программировании этой игры. Подумайте о проверке осмысленности предлагаемых дат… Кроме того, вставьте цикл ожидания, чтобы дать игроку время для ответных действий. Компьютер должен быть вежлив и должен спросить, кто будет начинать, по крайней мере, бросить «орла» или «решку», чтобы узнать, кому начинать…
?** Игра 18. Игра с 24 картами.
Расположим на столе 24 раскрытые карты: все карты с номерами от 1 до 6 обычной колоды, где туз считается за 1. Масти карт несущественны: двойка бубен имеет то же значение, что и двойка треф.
Каждый игрок при своем ходе берет со стола карту и складывает ее значение с суммой тех, которые были взяты ранее[14]. Первый, кто берет в точности 50 очков, выигрывает. Внимание: если при вашем ходе вы, взяв карту, не можете не превысить 50 очков, то вы проиграли. Если, например, ваш партнер увеличил сумму до 49 очков, а все тузы уже взяты, то вы проиграли: карту нужно брать, а ее значение больше единицы.
Это — вариант средневековой игры. Стратегия гораздо сложнее, потому что карт каждого сорта только 4. К этой игре нужно привыкнуть. Сперва компьютер выигрывает все партии подряд (любопытна реакция программиста: я счастлив, что моя программа меня обыгрывает). Но по прошествии нескольких партий уже я выигрываю. Тогда программу нужно улучшить.
?** Игра 19. Игра города Нима.
Ах! Эта нимская игра… кто ее не знает. Существует немало запрограммированных вариантов в большом числе публикаций и обзоров. Читатель может сказать мне, что этой игре здесь не место: если моя цель — заставить читателя программировать, то я проиграл с самого начала.
Ну, нет. Поскольку решения, предложенные в вышеупомянутых книгах (и, поскольку перечитывать их бесполезно, то я их имена и не указываю), очень плохо запрограммированы и совершенно не объяснены. Вам придется сделать лучше. Если вы знаете выигрывающую стратегию, то вам придется ее испытать, чтобы её проверить. Если вы ее не знаете, вы должны попробовать ее изобрести. Во всех случаях нужно программировать очень тщательно, чтобы не делать ненужных вычислений.
Напомним даже саму игру на тот очень мало правдоподобный случай, если вы ее еще не знаете. Это игра для двоих, и компьютер будет вашим партнером. На столе — кучи спичек в некотором количестве, и в каждой куче — некоторое количество спичек. Например, есть 5 кучек с 8, 13, 7, 5, 9 спичками.
Каждый игрок на своем ходе берет столько спичек, сколько хочет, из одной кучки, но он обязан взять хотя бы одну. Выигрывает тот, кто берет последнюю спичку. Вот партия, сыгранная от начала до конца. Компьютер начинает.
Исходное положение: 8, 13, 7, 5, 9
| Ход компьютера | Ваш ход |
| б, 13, 7, 5, 9 | 6, 3, 7, 5, 9 |
| б, 3, 7, 5, 7 | 2, 3, 7, 5, 7 |
| 2, 3, 7, 1, 7 | 2, 0, 7, 1, 7 |
| 2, 0, 4, 1, 7 | 2, 0, 3, 1, 7 |
| 2, 0, 3, 1, 0 | 2, 0, 2, 1, 0 |
| 2, 0, 2, 0, 0 |
Вы проиграли. Если вы возьмете две спички из одной кучки, то компьютер возьмет две из другой, так что и последнюю и потому выиграет. Если же вы возьмете одну спичку из одной кучки, то он возьмет одну из другой, и вы проигрываете на следующем ходе.
Мариенбадская игра является простым вариантом этой: проигрывает тот, кто берет последнюю спичку…
Этот род игр можно решительно осудить. Это — совершенно несправедливая игра. Выигрывающая стратегия существует. Если ваш противник ее не знает (как было в приведенном выше примере), то он обязательно проигрывает. Если же он ее знает, то он первый воспользуется усвоенной им выигрывающей стратегией, и вы ничего не сможете сделать. С другой стороны, даже если вы знаете выигрывающую стратегию, вы рискуете проиграть компьютеру, потому что вы не так хорошо считаете…
?** Игра 20. Игра Норткотта.
Вот менее известная игра, которую, однако, гораздо труднее программировать. Эта игра разыгрывается двумя участниками на прямоугольной площадке, разделенной на поля, как показано на рис. 12.
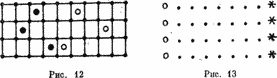
Каждый игрок располагает по шашке на каждой стропе, В начале черные шашки находятся на левых полях, белые — на правых. При каждом ходе игрок перемещает одну из своих шашек направо или налево на столько полей, сколько он хочет; но он не может переходить край игрового поля, и не может переходить за клетку, предшествующую противоположной шашке; шашки друг друга не берут и нельзя переходить занятое поле. Проигрывает тот, кто не может пошевелиться, потому что все его шашки загнаны между краем и противоположными шашками.
Размер игры значит очень мало. Я предпочитаю игру с тремя строками, но 4 и 5 — тоже очень хорошие числа. Длина строк несущественна. Выберите ее так, чтобы игра хорошо смотрелась.
На экране вы можете воспользоваться техникой, которая нам так часто служила. Пусть свободные клетки будут представлены точками, шашки одного из игроков — звездочками, а другого — 0. На рис. 13 воспроизведено начальное положение (4 строки, 9 полей на строке). Ход компьютера состоит просто в перемещении одной из его шашек (внимание: если ответ будет слишком быстрым, его, может статься, будет трудно воспринимать. Подумайте, как использовать цикл ожидания). Ход игрока может быть дан компьютеру в вг-де указания, на какой строке нужно переставить шашку и число полей при перемещении; положительное число указывает на приближение к противнику, отрицательное число означает отход к краю игрового поля. Все это очень просто,
?* Игра 21. Игра Кейлеса.
В наиболее простой форме эта игра разыгрывается со спичками, положенными в один ряд. Каждый игрок на своем ходе вынимает либо какую-то одну спичку из строки, либо две смежные спички. Это может разломать исходный ряд на несколько меньших рядов. Вот, например, начальная конфигурация (спички обозначены нулями), а затем — состояние игры через несколько ходов (точки обозначают места, оставшиеся пустыми).
Вначале:
0000000000000
После нескольких ходов;
.000..00.0000..
Выигрывает тот, кто берет последнюю спичку.
Игру можно легко распространить на случай нескольких исходных линий спичек. На каждом ходе игрок берет либо одну спичку, либо две соседние спички на линии, которую он выбрал.
Как и в предыдущих играх, подумайте о применении цикла, ожидания, чтобы у вас было время увидеть ответ компьютера. Как и в играх Нима и Норткотта, эта игра не очень-то справедлива. Компьютер выигрывает все партии, до крайней мере, если его противник не знает выигрывающей стратегии…
* Игра 22. Игра Сима.
Еще одна игра, тоже совершенно не равноправная для двух игроков — для компьютера и для вас.
Игра разыгрывается на листе бумаги, на котором обозначены 6 точек, являющихся вершинами правильного шестиугольника, помеченные буквами A, B, C, D, E, F. Естественно ожидать, что вашим партнером будет компьютер, и ему никакой бумаги не нужно, так что 6 точек появятся на экране.
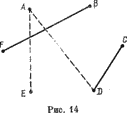
Каждый игрок при своем ходе проводит отрезок прямой, соединяющий еще не соединенные вершины. Нужно, чтобы следы отрезков, проведенных различными игроками, можно было отличить. На рис. 14 следы одного — сплошные, а у другого — штриховые. В запрограммированной игре именно компьютер берет на себя проведение отрезков. Скажите ему только названия вершин, которые вы хотите соединить. Он и проведет отрезок, причем такого типа, который вам присвоен. Затем он выберет вершины, которые он захочет соединить, и проведет свой собственный отрезок.
Проигрывает тот, кто первым построит треугольник из своих собственных отрезков. Так, на рис. 14 тот, кто проведет отрезок из тире между D и E, проигрывает, потому что он образует отрезок AED из тире, между тем как отрезок AC из тире безопасен: он образует, конечно, треугольник ACD, но одна из его сторон — сплошная, и поэтому он безвреден для обоих игроков.
Сумеете ли вы показать, что в этой игре всегда есть проигравший? (Нельзя так расположить все возможные отрезки, чтобы никакие три стороны их, одинаковым образом выполненные, не образовывали бы треугольника.) Сумеете ли вы предложить хорошую стратегию для компьютера? Если компьютер и игрок играют в равную силу и не совершают никаких ошибок, кто тогда выиграет? Начинающий? Или другой?
На моем микрокомпьютере, не имеющем графических средств, я был вынужден удовлетвориться проведением отрезков с помощью выстраивания в ряд букв там, где компьютер считал нужным их поставить. Картина получалась не очень красивой, но игра оставалась осуществимой и интересной. С графическим да еще с цветным экраном у вас должно получиться просто загляденье, Но не забывайте поговорку Анри Ледгара [LED]:
Не занимайтесь формой вывода результатов, пока ваша программа не окажется правильной.
Когда ваша программа окажется правильной, тщательно отработайте форму вывода результатов.
? Игра 23. Спички Бергсона.
Нет, этот великий философ не играл в такие игры — по крайней мере, насколько я знаю. Эту игру предложил мне М. Дюма,: профессор лицея Бергсона. Еще одна игра для двоих, в которой компьютер — ваш неумолимый партнер. Потому что если вы обнаружите выигрывающую стратегию, то компьютер не оставит вам никаких шансов, ведь у него и память есть…
На столе — кучка спичек (достаточно большая: вначале — по крайней мере 50). Каждый игрок при своем ходе берет спички из кучки. Нужно взять по крайней мере одну и не более чем вдвое больше, чем взял предыдущий игрок. На первом ходе можно взять одну или две спички. Выигрывает тот, кто берет последнюю спичку.
Вот последовательность возможных ходов. Вначале — 50 спичек.
| Игрок А берет | Остается | Игрок Б берет | Остается |
| 1 | 49 | 2 | 47 |
| 4 | 43 | 8 | 35 |
| 16 | 19 | 19 | выиграл |
На каждом ходе, кроме последнего, каждый из игроков брал максимальное возможное количество, и игрок Б легко выиграл, взяв на последнем ходе 19 спичек, на что имел полное право, так как 1 ? 19 ? 2 ? 16 = 32. Конечно, это очень плохая стратегия. Вот другая партия:
| Игрок А берет | Остается Игрок Б берет | Остается |
| 3 | 47 | 4 43 |
| 1 | 42 | 2 40 |
| 1 | 39 | 1 38 |
| 1 | 37 | 2 35 |
| 1 | 34 | 2 32 |
| 3 | 29 | 6 23 |
| 2 | 21 | 4 17 |
| 4 | 13 | 2 11 |
| 3 | 8 |
Игрок А близок к победе. Если Б возьмет 3 спички и останется 5, то А имеет право взять последнюю. Это тем более верно, если Б возьмет более чем 3 спички (4, 5 или 6). Игрок Б не может взять больше и во всех случаях дает игроку А все права, чтобы он мог взять последнюю спичку). Единственными случаями, подлежащими обсуждению, остаются поэтому случаи, когда Б берет одну или две спички.
Если Б берет одну, то остается 7, А берет 2 и остается 5. Если Б после этого берет более одной, то А берет последнюю; если Б берет одну и остается 4, то А берет одну и остается 3; Б может взять только одну или две, и кончает игру А.
Если Б берет 2 и остается 6, то. А берет одну и остается 5, и А выигрывает тем же способом.
Я так подробно разбирал этот пример, чтобы познакомить вас с основными идеями. Тщательно изучите этот пример. Всегда ли игрок А заведомо выигрывает, как только он оставляет в куче 8 спичек…
Не предпринимайте здесь слишком глубокого изучения выигрывающей стратегии. Мы к ней еще вернемся ниже. Устройте только, чтобы ваш компьютер выигрывал при приведенных выше условиях, если старт для него благоприятен…
Вы легко сообразите, как представить эту игру на экране,
??** Игра 24. Гениальный отгадчик.
Вы уже сделали гениального ответчика; эта игра сложнее. Составьте программу для отыскания комбинаций, задуманных гениальному отгадчику. Вы можете идти двумя путями:
— вы выбрали комбинацию. Компьютер предлагает вам свою, затем читает число черных и белых шашек, которые получаются из того, что он вам предложил. Он должен найти ответ за наименьшее возможное число ходов;
— вы выбрали исходную комбинацию и сообщили ее компьютеру. Дальше все идет автоматически. Он выбирает некоторую комбинацию, определяет число черных и белых шашек, сообщает это все, затем переходит к следующей комбинации — пока не найдет ответ. Компьютер честен и не хитрит: он не использует того, что он знает задуманную комбинацию…
Вы скажете, что это неинтересно. Но это не так. Во-первых, стратегия поиска является вызовом для способности мышления. Мне пришлось немного подумать, чтобы получить в свое время разумный ответ с 6 позициями и 8 цветами. Попробуйте сами и убедитесь! С другой стороны, для гениального отгадчика существует проблема эффективного начала, В программе, составленной мною, я сам выбираю первые испытательные комбинации. Я смотрел, сколько было систематических попыток и каковы они были. Это позволило понять, насколько важен начальный выбор и может ли он сильно влиять на результаты. Это — хорошее орудие экспериментирования. И это очень легко устроить. Компьютер запрашивает вас, сколько опытов априори вы хотите осуществить. Затем он запрашивает у вас начальные комбинации, число которых он только что прочел. После этого компьютер предпринимает систематическое исследование, какая из предложенных комбинаций должна быть оставлена.
Чтобы преуспеть, вам нужен хороший метод, и программировать нужно очень тщательно.
?** Игра 25. Погоня за сокровищем.
Любой начинающий в информатике мечтает сделать программу — чемпиона мира по шахматам… Я и сам видел несознательных, бросавшихся на эту задачу. Чтобы утешить их, нужно сказать, что это — одно из больных мест истории информатики. Компьютеры были еще электронными монстрами, напичканными радиолампами, которые приходилось охлаждать кубическими метрами воды, когда Герберт Симон (недавний Нобелевский лауреат по экономике) уже сделал примечательные предсказания:
— через 10 лет чемпионом мира по игре в шахматы станет компьютер, по крайней мере если правила не будут запрещать им участвовать в соревнованиях;
— через 10 лет компьютер обнаружит и докажет новую важную математическую теорему;
— через 10 лет большая часть диссертаций, выпускаемых по психологии, будет облечена в форму программ для компьютеров или качественных комментариев к примечательным особенностям компьютерных программ (Герберт А. Симон, Аллан Кьюзлл: Эвристическое решение задач: следующее продвижение в исследовании операций. «Operations research», т. 6, январь-февраль 1958, с. 6),
И через 25 лет с момента предсказания у нас не возникло проблемы запрещать доступ компьютеров к шахматным чемпионатам, они не представляют серьезной угрозы. Да, одна из программ выиграла партию у чемпиона (каждый человек имеет право ошибиться; конечно, это относится и к чемпиону. Он был очень усталым). Ни одна важная теорема машиной не обнаружена, Что же касается диссертаций по психологии, то, может быть, даже хорошо, что предсказание Симона не оправдалось… Очень больно видеть, до какой степени информатика является благоприятным местом для ложных предсказаний. Сколько их нам обещали, этих чудес, которых мы так никогда и не увидели! Два года тому назад, во время Сикоба, журналист первой программы Французского телевидения показывал чудесную машину. Она была удивительно похожа на фотокопировальную. Он приподнял крышку, нашел там букву, нажал кнопку «и теперь буква зарегистрирована и мы ее легко узнаем, когда это потребуется». Фантастика! Покончим с этими мучительными сеансами поисков буквы этим господином, который два месяца назад подписал по этому делу контракт, номер которого я забыл… Но это был не господин, это была дама, и это было не два месяца назад, это был прошлый февраль. Больше никто не говорил об этой волшебной машине. Как же может случиться, что молодые люди не имеют никакого здравого смысла в информатике, так что можно без опаски предсказывать самые фантастические и самые неправдоподобные вещи, не вызывая ни смеха, ни краски стыда. «Мы подготовим 100000 преподавателей за пять лет…» Но это — совсем другая история, как говорил Киплинг.
Вернемся-ка к шахматам. Речи нет о лом, чтобы вы ими занялись; это выше понимания любителя, даже самого талантливого. Но я хочу предложить вам нечто, что все же имеет какое-то отношение к шахматам и одновременно может позволить упражняться в постановке пьесы.

Я представляю шахматную доску на рис. 15 как на экране своего микрокомпьютера в виде квадратной таблицы с 64 полями, которые представлены точками. На шахматной доске в левом верхнем углу расположена черная ладья (помеченная крестом), а в нижнем правом углу — белая ладья (помеченная звездочкой). Тринадцать шашек, помеченных маленькими кружочками, случайным образом расположены на игровом поле. Компьютер перемещает черную ладью ?, а вы — белую ладью *. Каждый игрок на своем ходе передвигает ладью, как при игре в шахматы; только на поля на той же строке или в том же столбце. Можно взять шашку и встать на место, которое она занимала; тогда эта шашка выходит из игры. Можно, взять противоположную ладью, если оказывается возможным попасть на занимаемое ею место. Тогда игра останавливается, и тот, кто взял чужую ладью, и есть победитель. В противном случае игра останавливается, когда больше шашек нет. Тот, кто взял больше шашек, и есть победитель.
Вам необходимо указывать компьютеру, какой именно ход вы хотите сделать. Вы можете, например, отметить строки цифрами, а столбцы — буквами, как на рисунке. Ваш первый ход будет, без сомнения, на H2 или B1…
Стратегия совершенно не очевидна. У вас много возможностей. Не так много, конечно, как в шахматной игре, но достаточно для того, чтобы вам пришлось заняться всерьез, что бы написать программу, которую было бы трудно побить.
Если вы при этом достигли совершенства, почему бы не попробовать ее вариант, который не должен вызывать намного больше затруднений (???): та же задача, но ладьи заменены конями.
*** Игра 26. Могущественная четверка.
Эта игра продается на рынке в другой форме. Она происходит в прямоугольном пространстве с 5 строками и 7 столбцами. Игра ориентирована, у нее есть низ и верх. Игровые позиции суть наинизшие свободные места в каждом столбце. Каждый игрок на своем ходе помещает свой отличительный знак на одно из игровых полей: например, один ставит крестики (+), другой — нолики (0). Первый, кто поставит на одной линии четыре принадлежащих ему знака — либо горизонтально, либо вертикально, либо по диагонали — выигрывает. На рис. 16 будем считать, что нолики при игре ставит тот игрок, чей ход именно сейчас. Если он не сыграет немедленно в пятом столбце, то его противник выиграет следующим ходом. По диагонали, начинающейся у основания четвертого столбца и идущей влево и вверх, есть три нолика, но единственное игровое поле в первом столбце обозначено точкой, и немедленно реализовать продолжение линии поэтому нельзя. Очевидно, что его противник не имеет никакого желания служить ему подставкой при пополнении первого столбца вместо того, чтобы заниматься разыгрыванием мест, допускающих продолжение линии…
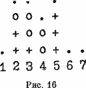
Эту игру, производную от вошек, программировать намного проще, потому что всего полей только 35, и только 7 из них являются игровыми полями на каждом ходе. Это существенно ограничивает работу. В реализованной мною версии ответ микрокомпьютера практически мгновенный (порядка секунды). Я не думаю, что я располагаю программой-чемпионом, я не очень хорошо знаком с атим родом игр…
- Азартные игры
- Могу ли я изменить или отключить звуки, которые проигрываются при запуске Windows, щелчке кнопкой мыши на папке и т. д.?
- При попытке скачать из Интернета МР3-файл запускается Проигрыватель Windows Media. Но мне нужно просто скачать файл. Как...
- 8.4. Оформляем интерфейс проигрывателя
- Не могу просматривать DVD-фильмы, хотя игры на DVD работают. В чем дело?
- Как просмотреть фильм другим проигрывателем, не тем, который установлен по умолчанию?
- Запуск игры
- 5. Стратегия без игры (выигрывающие стратегии)
- Урок 4.5. Проигрыватель Windows Media
- Основные возможности проигрывателя
- Режимы работы проигрывателя




