Книга: Основы классической криптологии. Секреты шифров и кодов
Квадрат Эйлера
Квадрат Эйлера
Известный математик, астролог и криптограф Леонард Эйлер, долгое время работавший в России в XVIII веке, является автором известной таблицы, состоящей из восьми столбцов и восьми строк.
Все клетки так называемого квадрата Эйлера заполнены числами от 1 до 64 так, что сумма всех чисел, расположенных в одном столбце и в одной строке, составляет одно и то же число, а именно 260. Более того, если данную таблицу разделить на четыре квадратные таблицы, то и в каждой из них сумма чисел в ячейках одного столбца и одной строки также будет одинакова и составит 130. Таким же свойством обладает и квадрат размером 4x4, составленный из ячеек, расположенных в центральной части большой таблицы.
Порядок заполнения ячеек в квадрате Эйлера выглядит следующим образом:
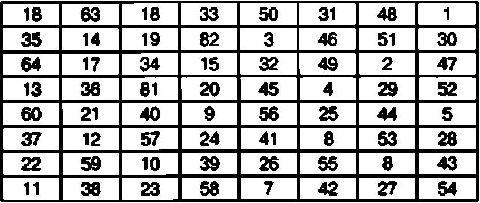
Нетрудно заметить, что с математической точки зрения данная таблица не является классическим магическим квадратом, поскольку суммы чисел в ячейках, образующих диагонали, не равны между собой. В то же время квадрат Эйлера можно использовать для шифрования сравнительно длинных сообщений, используя алгоритм шифрования, рассмотренный ранее для классических магических квадратов.
- Простой числовой шифр
- Шифр гласных букв
- Календарный шифр
- 5.5. Книжные шифры
- Простой книжный шифр
- Усовершенствованный книжный шифр
- 5.6. Тайны решеток и таблиц
- Простая шифровальная таблица
- Таблица с паролем
- Квадрат Полибия
- Шифр «Большой крест»
- 5.7. Перестановки в таблицах
- Простая перестановка
- Перестановка с паролем
- Двойная перестановка
- 5.8. Магические квадраты
- Простейший магический квадрат
- Индийский квадрат
- Квадрат Эйлера
- Магический квадрат 9x9
- 5.9. Трафарет в системах шифрования
- Простой шифр с трафаретом
- Решетка Кардано
- 5.10. Биграммные шифры
- Шифр «Двойной квадрат»
- Магический квадрат 9x9
- Квадрат возражений
- 20. Квадратный трехчлен, или Пакет Для Алгебраических Вычислений
- 22. ? эр Квадрат, или Арифметические вычисления с высокой точностью
- 7. Магический квадрат
- 8. Магический квадрат из простых чисел
- Квадрат Полибия
- Критерий хи-квадрат
- Метод средних квадратов
- Квадратичное зондирование
- Новое и последовательное – квадратура круга?
- 1.2. «Квадратная» организация




