Книга: Основы классической криптологии. Секреты шифров и кодов

Индийский квадрат

В одном из древних индийских храмов исследователи обнаружили квадратную таблицу, которая при более подробном изучении оказалась одним из самых первых известных магических квадратов. По мнению некоторых историков, эта таблица была создана в XII веке.

Ячейки данной таблицы, состоящей из четырех столбцов и четырех строк, заполнены числами от 1 до 16 так, что сумма всех чисел, расположенных в одном столбце, в одной строке и на одной диагонали, составляет одно и то же число, а именно 34. Более того, сумма чисел в четырех ячейках, образующих квадратные таблицы внутри данного магического квадрата, также составляет 34.

Порядок заполнения ячеек в этой таблице выглядит следующим образом:

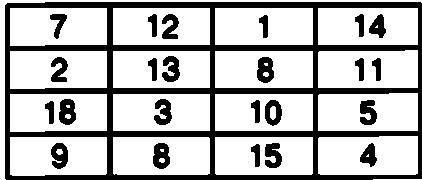
Естественно, что такой магический квадрат также можно использовать для шифровки короткого сообщения, содержащего до шестнадцати знаков.

В качестве примера зашифруем, например, открытый текст СЕКРЕТНАЯ ВСТРЕЧА. Для шифрования данного сообщения с использованием рассмотренного ранее алгоритма необходимо сначала вставить в ячейки таблицы вместо цифр буквы открытого текста. При этом вместо цифры 1 в соответствующую ячейку следует вставить первую букву открытого текста, в рассматриваемом примере это будет буква С. Вместо цифры 2 в соответствующую ячейку следует вставить вторую букву открытого текста, то есть букву Е, и так далее.

В результате такой замены шифровальная таблица примет следующий вид:

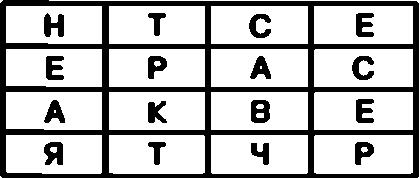
Теперь для создания криптограммы достаточно последовательно выписать буквы из ячеек первой строки, затем из ячеек второй строки и так далее.

В окончательном виде криптограмма для открытого текста СЕКРЕТНАЯ ВСТРЕЧА будет выглядеть так:

НТСЕ ЕРАС АКВЕ ЯТЧР

Для того чтобы расшифровать эту шифрограмму, получатель сообщения должен сначала заполнить таблицу известных ему размеров буквами криптограммы, а затем из соответствующих ячеек выписать буквы открытого текста в порядке, определяемом цифрами используемого магического квадрата.

По утверждению некоторых источников, классических магических квадратов размером 4x4 существует всего 12. При этом другие магические квадраты тех же размеров могут быть образованы из первоначального, например с помощью поворота таблицы или отражения строк и столбцов. Общее число таких производных магических квадратов разными специалистами оценивается от нескольких сотен до нескольких тысяч. С учетом того, что любой из упомянутых магических квадратов может быть использован для шифрования сообщения, задача взлома шифра для незаконного пользователя с помощью подбора необходимой таблицы вручную становится практически невыполнимой.

Оглавление книги