Книга: Фундаментальные алгоритмы и структуры данных в Delphi

Критерий хи-квадрат

Критерий хи-квадрат

Представьте себе, что есть две монеты, над которыми поработал мошенник. Каким образом можно доказать, что монеты имеют смещенный центр тяжести? Конечно, наш предполагаемый мошенник мог быть достаточно глупым и просто сбалансировать монеты таким образом, чтобы они всегда падали решкой вверх. Но такой мошенник был бы давным-давно пойман, а более изобретательный мошенник вполне мог бы остаться на свободе. Давайте бросим две монеты, скажем, 100 раз, и внесем полученные данные в таблицу. Полученная таблица может выглядеть следующим образом (см. табл. 6.1):

Таблица 6.1. Результаты бросания 100 раз двух монет со смещенным центром тяжести

В таблице 6.1 для каждого возможного события приведена вероятность его возникновения и, кроме того, указано ожидаемое количество появлений каждого из событий для 100 бросков. (Ожидаемое количество появлений событий представляет собой просто результат умножения вероятности на общее количество событий.)

Одного взгляда достаточно, чтобы сказать, что две решки выпадают чаще, чем этого следует ожидать, однако достаточно ли велико отклонение, чтобы можно было сказать, что монеты имеют смещенный центр тяжести? Давайте посмотрим на разброс (т.е. отличие) полученных и ожидаемых результатов. Чтобы выделить разности и избавиться от отрицательных значений, возведем их в квадрат. Сумма полученных квадратов разностей и будет служить оценкой случайности результатов проведенных тестов. В нашем случае вычисление суммы квадратов разностей дает 26 (= 3(^2^) +1(^2^) + (-4)(^2^)). Но подождите-ка минутку, нам нужно каким-то образом учесть вероятность возникновения каждого события. Так для события "орел и решка" квадрат разности должен быть больше, чем для события "две решки", хотя бы только потому, что первое событие должно происходить чаще. Другими словами, разница 3 для события "две решки" будет намного более значительна, чем разница 1 для события "орел и решка". Поэтому давайте разделим каждый квадрат разности на ожидаемое количество появлений соответствующего события. Новая сумма будет вычисляться следующим образом:

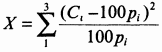
где С(_i_) - наблюдаемое количество, a p(_i_) - вероятность возникновения события i. Для наших данных значение X будет равно 1.02. Полученная нами сумма известна под названием критерия хи-квадрат (chi-squared value). Полученное значение можно найти в таблице стандартного распределения хи-квадрат (см. табл. 6.2).

Таблица 6.2. Процентные точки распределения хи-квадрат

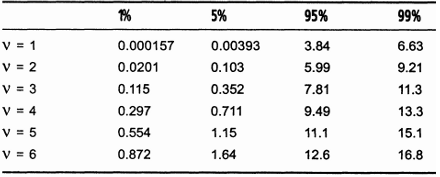
Вид таблицы слегка пугает, но понять ее совсем не сложно. Значения, приведенные в таблице, представляют собой значения распределения хи-квадрат для v степеней свободы (греческая буква v - это стандартный символ для обозначения степеней свободы). В свободной интерпретации можно сказать, что значение степеней свободы на единицу меньше количества возможных типов событий. В нашем случае возможны три типа событий: "две решки", "орел и решка" и "два орла". Следовательно, для нашего эксперимента количество степеней свободы будет равно 2. Строка для v = 2 содержит четыре значения - по одному значению в каждом из четырех столбцов. Значение в столбце 1% (0.0201) можно интерпретировать следующим образом: "Значение критерия X должно быть меньше 0.0201 только 1% времени". Другими словами, при повторении эксперимента 100 раз только примерно в одном из них будет получено значение X, меньшее 0.0201. Если будет обнаружено, что во многих экспериментах будет получено значение меньше 0.0201, можно будет с достаточно высокой степенью уверенности сказать, что бросание монет не является случайным событием, т.е. монеты имеют смещенный центр тяжести. То же самое можно сказать и для столбца 5%. О столбце 95% можно сказать, что значение параметра X должно быть меньше 5.99 примерно 95% времени или, что эквивалентно, значение параметра X должно быть больше 5.99 примерно 5% времени. Аналогичные рассуждения справедливы и для столбца 99%.

Полученное нами значение параметра X попадает в диапазон от 5% до 95%, т.е. на его основе мы не можем прийти к четкому заключению о смещенном центре тяжести монет. Приходится предполагать, что монеты являются настоящими (без всяких "хитростей"). Если же, с другой стороны, значение X было равно 10, можно было бы сказать, что такая ситуация может складываться не более чем в 1% экспериментов (10 больше чем 9.21 - значения для столбца 99%). Это послужило бы веским доказательством того, что монеты имеют смещенный центр тяжести. Конечно, потребуется провести большее количество экспериментов, и посмотреть, каким образом получаемые данные соотносятся со стандартным распределением хи-квадрат. По такому расширенному набору данных можно будет более точно оценить случайность получаемых данных. Не хотелось бы делать выводы, основываясь на результатах, которые согласно теории вероятностей, хотя и редко, но все же могут быть получены.

Как правило, при оценке случайного характера получаемых результатов берется одна и та же граница с каждого конца распределения хи-квадрат, скажем, 5% и 95%, и утверждается, что эксперимент является достоверным на уровне 5%, если данные эксперимента не попадают в эти границы, и недостоверным на уровне 5% - в противном случае.

До сих пор мы не упоминали еще один аспект: какое количество отдельных событий нужно генерировать? В нашем примере с монетами их было 100. Достаточно ли такого количества? Или можно обойтись и меньшим объемом экспериментов? Или же количество событий должно быть больше? К сожалению, четкого ответа на поставленные вопросы не существует. Кнут (Knuth) утверждает, что хорошим практическим методом для определения достаточности объема экспериментов является следующее: количество ожидаемых событий каждого типа должно быть не менее пяти (в нашем случае ожидаемыми значениями являются 25, 50 и 25, следовательно, объем нашего эксперимента вполне достаточен для оценки случайности результатов), но чем больше событий каждого типа, тем лучше [11].

Давайте оставим наши монеты в покое и вернемся к гипотетической последовательности случайных чисел. Воспользуемся всеми только что полученными знаниями. Определим количество вхождений каждого числа, вычислим значение параметра X и посмотрим, как оно соответствует распределению хи-квадрат с девятью степенями свободы (для последовательности однозначных чисел возможно выпадение одного из 10 чисел;

таком образом, количество степеней свободы будет на единицу меньше, т.е. 9). Минимальный объем экспериментов должен составлять, по крайней мере, 50 чисел (чтобы количество разных чисел было не менее 5), хотя чем длиннее последовательность, тем лучше.

Можно пойти даже дальше. Если рассматривать последовательность как серию пар чисел от 00 до 99, считая каждую пару отдельным событием, ее можно будет разбить на 100 типов событий. Следовательно, количество степеней свободы будет равно 99. Вероятность выпадения каждой пары составляет 1:100. Таким образом, для обеспечения возможности оценки случайности последовательности она должна содержать не менее 500 пар (1000 чисел).

Более того, можно использовать не пары чисел, а тройки, но в этом случае понадобится проводить еще больший объем экспериментов. Существуют и другие виды тестов, но перед их рассмотрением давайте выясним, как можно генерировать случайные числа. После изучения нескольких генераторов последовательностей случайных чисел можно будет прогнать тесты на результатах их работы.

Еще раз хотелось бы повторить, что детерминированные алгоритмы не могут генерировать последовательности случайных чисел, аналогичные получаемым при бросках игрального кубика или при подсчете количества бета-частиц во время распада радиоактивного материала. Детерминированные алгоритмы на основе одинаковых исходных данных будут генерировать одни и те же последовательности чисел. Если, например, генератор X, основанный на четко определенном алгоритме, для начального числа 12 345 678 генерирует случайное число 65 584 256, то даже через пять месяцев тот же генератор X при том же начальном числе даст значение 65 584 256. Следовательно, в вычислении последовательности случайных чисел нет случайности, но с помощью статистических тестов можно показать, что последовательность чисел, генерируемая подобным образом, содержит случайные числа.

Более того, в некоторых случаях повторяемость последовательности случайных чисел бывает даже желательна. Она позволяет использовать генератор для многократного воспроизведения одной и той же последовательности. Такая возможность бывает необходимой в процессе отладки с целью воспроизведения ошибки.

Оглавление книги