Книга: Основы классической криптологии. Секреты шифров и кодов

Простейший магический квадрат

Как известно, чем меньше столбцов и строк в квадратной таблице, тем меньше вариантов построения на ее основе магического квадрата Так, например, для таблицы, состоящей из трех столбцов и трех строк, известен всего лишь один вариант заполнения ячеек цифрами от 1 до 9, в результате которого получится магический квадрат. Такая таблица будет выглядеть так:

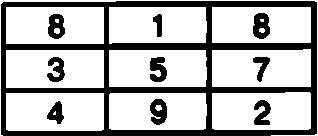
Нетрудно подсчитать, что сумма цифр в каждом столбце, в каждой строке и в каждой большой диагонали составляет одно и то же число и равна 15.

При использовании шифров, основанных на магических квадратах, один из простейших алгоритмов шифрования заключается в том, что в ячейки таблицы вместо цифр магического квадрата вписываются по порядку буквы открытого текста. Так, например, вместо цифры 1 в соответствующую ей ячейку следует записать первую букву сообщения, вместо цифры 2 — вторую букву, вместо цифры 3 — третью букву и так далее.

В качестве примера зашифруем с помощью этого магического квадрата открытый текст РАЗВЕДЧИК При этом в ячейку с цифрой 1 следует записать букву Р, в ячейку с цифрой 2 — букву А, в ячейку с цифрой 3 — букву 3 и так до конца сообщения. В результате таблица примет следующий вид:

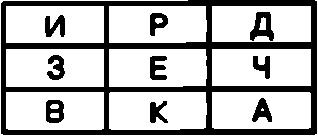
Теперь для создания криптограммы достаточно последовательно выписать буквы из ячеек первой строки, затем из ячеек второй строки и так далее.

В окончательном виде криптограмма для открытого текста РАЗВЕДЧИК будет выглядеть так:

ИРД ЗЕЧ ВКА

Получив такую шифрограмму, получатель для расшифровки сообщения должен сначала заполнить таблицу буквами криптограммы, а затем из соответствующих ячеек выписать буквы открытого текста в порядке, определяемом цифрами используемого магического квадрата.

Необходимо отметить, что утверждение о существовании лишь одного магического квадрата размером 3x3 для цифр от 1 до 9 не касается случаев, когда другие магические квадраты могут быть образованы из первоначального с помощью поворота таблицы или отражения строк и столбцов.

Один из таких производных квадратов может выглядеть следующим образом:

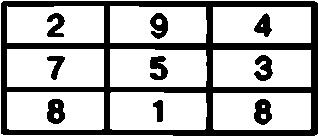
Такой магический квадрат также с успехом можно использовать для шифрования коротких сообщений в соответствии с приведенным выше алгоритмом.

Оглавление книги