Книга: Новый ум короля: О компьютерах, мышлении и законах физики
Временна?я асимметрия в редукции вектора состояния
Временна?я асимметрия в редукции вектора состояния
По-видимому, нам действительно ничего не остается, как заключить, что ПКТГ должна быть асимметричной во времени теорией, одним из следствий которой является ГВК (или что-то вроде этого). Как же асимметричная во времени теория может получиться из симметричных во времени ингредиентов: квантовой теории и общей теории относительности? Есть, оказывается, несколько технических способов достижения этой цели, и ни один из них не исследовался достаточно глубоко (см. Аштекар и др. [1989]). Но я собираюсь подойти к проблеме с другой стороны. Как я уже отмечал, квантовая теория «симметрична во времени», но это в действительности относится только к части U теории (уравнению Шредингера и т. д.). Обсуждая временну?ю симметрию физических законов в начале главы 7, я умышленно избегал упоминания части R (коллапс волновой функции). Согласно преобладающей точке зрения R тоже должна быть, по-видимому, симметричной во времени. Своим существованием эта точка зрения может, в частности, быть обязана нежеланию признавать в R реальный независимый от U «процесс», вследствие чего из временно?й симметрии U должна бы также вытекать временная симметрия R. Я хотел бы возразить, что это не так: R асимметрична во времени — по крайней мере, если считать R просто процедурой, принятой физиками для расчета квантово-механических вероятностей.
Я сначала напомню вам используемую в квантовой механике так называемую процедуру редукции вектора состояния (R) (см. рис. 6.23). Рис. 8.1 иллюстрирует (условно) характер предполагаемой эволюции вектора состояния |?) в квантовой механике.
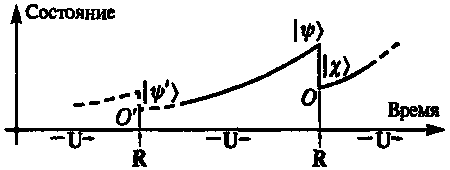
Рис. 8.1. Временная эволюция вектора состояния: гладкая унитарная эволюция U (в соответствии с уравнением Шредингера), перемежаемая с разрывной редукцией R вектора состояния
Как видим, этот характер довольно своеобразный: считается, что бо?льшую часть времени эволюция происходит в соответствии с унитарной эволюционной процедурой U (уравнение Шредингера), но в некоторые моменты времени, когда предполагается, что происходит «наблюдение» (или «измерение»), применяется R-процедура и вектор состояния скачком переходит в другой вектор состояния, |X), где |X) представляет собой одну из двух или нескольких ортогональных альтернативных возможностей |X), |?), |?)…, определяемых природой конкретного производимого наблюдения О. Тогда вероятность р скачкообразного перехода от |?) к |X) определяется уменьшением квадрата длины |?)2 вектора |?) при проекции |?) (в гильбертовом пространстве) на направление вектора |X) (Математически это равно величине уменьшения |X)2 при проекции вектора |X) на направление |?).) В таком виде эта процедура оказывается асимметричной во времени, поскольку сразу же после выполнения наблюдения О вектор состояния должен принадлежать к заданному множеству |X), |?), |?)…, возможных значений, определяемыхО, в то время как непосредственно перед наблюдением О вектор состояния должен был иметь значение |?), которое не обязано быть равным ни одному из элементов упомянутого множества. Однако, это всего лишь кажущаяся асимметричность и она может быть устранена, если посмотреть на эволюцию вектора состояния с другой точки зрения. Рассмотрим квантово-механическое решение, обращенное во времени. Это экстравагантное описание проиллюстрировано на рис. 8.2.
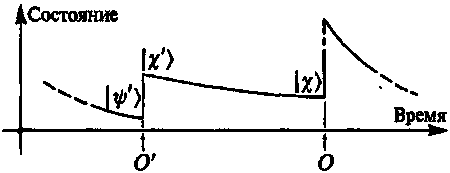
Рис. 8.2. Более экстравагантное изображение эволюции вектора состояния, описанное вспять по времени. Расчетная вероятность, связывающая наблюдение в точке О с наблюдением в точке О', такая же, как и в случае, изображенном на рис. 8.1, но к чему относится это вычисленное значение?
Мы предполагаем, что вектор состояния равен |X) непосредственно передО, а не сразу после этого наблюдения, и применим процедуру унитарной эволюции вспять по времени вплоть до момента предыдущего наблюдения О'. Предположим, что в результате обратной эволюции мы получим состояние, описываемое вектором |X') (сразу же после наблюдения О'). В нормальном описании эволюции вперед во времени, изображенном на рис. 8.1, сразу же вслед за О' мы имели другое состояние |?') (результат наблюдения О', при котором эволюция вперед во времени вектора |?') переводит его в |?) в момент наблюдения О). Теперь в нашем обращенном во времени описании у вектора |?') тоже есть своя роль: он представляет состояние системы непосредственно перед О'. Вектор состояния |?') соответствует состоянию, фактически наблюдавшемуся в точке О', так что с «обращенной» точки зрения мы рассматриваем |?') как результат наблюдения О' в обращенном вспять времени. Расчетное значение квантовомеханической вероятности р', связывающее результаты наблюдений в точках О и О', теперь определяется уменьшением величины |X'|2 при проекции |X') в направлении |?') (что равно уменьшению |?'|2 при проекции |?') в направлении |?')). То, что мы получим то же самое значение, что и раньше, является фундаментальным свойством оператора U[193].
Таким образом, может создаться видимость установления симметричности во времени квантовой теории даже в случае, когда помимо обычной процедуры унитарной эволюции U учитывается также и разрывный процесс, описываемый процедурой редукции R вектора состояния. Это, однако, неверно. Квантовая вероятность р описывает — независимо от того, как она рассчитывается — вероятность получить результат (а именно, |X)) в точке О при условии определенного результата (а именно, |?')) в точке О'. Эта вероятность не обязательно равна вероятности получить данный результат в точке О' при условии данного результата в точке О, а ведь именно последнюю вероятность[194] и должна определить обращенная во времени квантовая механика. Просто удивительно, до чего много физиков молчаливо полагают эти две вероятности равными друг другу. (Я сам этим грешил — см. Пенроуз [1979б], с. 584.) Однако наиболее вероятно, что эти две вероятности совершенно различны и только первая из них правильно определяется в рамках квантовой механики!
Давайте поясним эту ситуацию на простом конкретном примере. Предположим, что у нас есть лампа L и фотоэлемент (то есть, детектор фотонов) Р. Между L и P разместим полупосеребренное зеркало М, наклонив его под углом равным, скажем, 45° к линии, соединяющей точки L и Р (рис. 8.3).
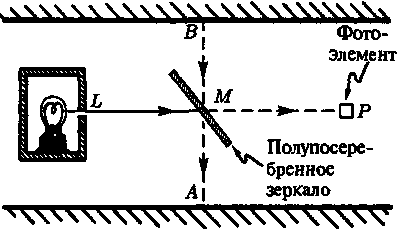
Рис. 8.3. Необратимость во времени R-процедуры в простом квантовом эксперименте. Вероятность регистрации фотона фотоэлементом при условии излучения фотона источником равна в точности одной второй, но вероятность излучения фотона источником при условии, что фотоэлемент зарегистрировал фотон, заведомо не равна одной второй
Предположим, что лампа время от времени случайным образом испускает фотоны, и что конструкция ее такова (в ней используются параболические зеркала), что фотоны всегда оказываются очень точно нацеленными на Р. При каждом попадании фотона на фотоэлемент последний регистрирует это событие, причем мы предполагаем, что устройство срабатывает со 100 %-ной надежностью. Предположим также, что каждый факт излучения фотона регистрируется в точке L и тоже со 100 %-ной надежностью. (Ни одно из этих идеализированных требований не противоречит принципам квантовой механики, хотя практическое достижение такой эффективности может представлять определенные трудности.)
Свойства полупосеребренного зеркала М таковы, что оно отражает в точности половину попадающих на него фотонов и пропускает остальную половину. Правильнее рассматривать это с точки зрения квантовой механики. Волновая функция фотона падает на зеркало и расщепляется на две волновых функции. Амплитуда отраженной части волны равна 1/?2, а амплитуда прошедшей части волны тоже равна 1/?2. Обе части волновой функции должны считаться «сосуществующими» (при нормальном описании вперед по времени) до того момента, когда предполагается имевшим место «наблюдение». В этой точке ситуация с одновременно сосуществующими альтернативами разрешается (в пользу одной или другой) фактически реализованной альтернативы с вероятностями, равными квадратам (модулей) соответствующих амплитуд, а именно (1/?2)2 = 1/2 в обоих случаях. После выполнения наблюдения вероятности отражения или прохождения фотона действительно оказываются равными одной второй.
Посмотрим теперь, как все это соотносится с нашим экспериментом. Предположим, что зарегистрирован факт излучения фотона лампой L. Волновая функция фотона расщепляется на зеркале и приходит в точку Р с амплитудой, равной 1/?2, поэтому фотоэлемент либо регистрирует фотон, либо не регистрирует его — и то и другое с вероятностью, равной одной второй. Другая часть волновой функции фотона попадает в точку А на лабораторной стене (см. рис. 8.3) и тоже с амплитудой 1/?2. Если фотоэлемент Р не регистрирует событие, то фотон следует считать попавшим в лабораторную стену в точке А. Если бы в точке А находился другой фотоэлемент, то он регистрировал бы фотон всякий раз, когда фотоэлемент Р не регистрирует фотон, и не регистрировал бы фотон всякий раз, когда фотоэлемент регистрирует фотон. В этом смысле нет никакой необходимости устанавливать фотоэлемент в точке А. Мы можем определить, что сделал бы фотоэлемент в точке А, будь он там установлен, просто глядя на фотоэлементы в точках L и Р.
Теперь должно стать ясно, как выполняются расчеты в квантовой механике. Зададимся вопросом:
«Если известно, что лампа L сработала, то какова вероятность того, что сработал фотоэлемент Р?»
Для ответа на этот вопрос учтем, что имеется амплитуда, равная 1/?2 для фотона, прошедшего путь LMP, и амплитуда, равная 1/?2, для фотона, прошедшего путь LMA. Возведя эти амплитуды в квадрат, получаем соответствующие вероятности, равные 1/2 и 1/2, попадания фотона в точки Р и А соответственно. Следовательно, на наш вопрос квантовая механика дает ответ, равный
«одной второй».
И действительно, именно такой результат получился бы в случае проведения реального эксперимента.
Мы могли бы с таким же успехом использовать экстравагантную процедуру «с обращенным вспять временем» и получили бы тот же самый результат. Предположим, что мы зафиксировали факт срабатывания фотоэлемента в точке Р. Рассмотрим направленную вспять во времени волновую функцию фотона в предположении, что фотон в конце концов приходит в точку Р. Отслеживая эволюцию процесса назад во времени, мы видим, что фотон движется назад от Р, пока не достигнет зеркала М. В этой точке происходит бифуркация волновой функции и мы имеем амплитуду 1/?2 того, что фотон достигнет лампы L, и амплитуда 1/?2 того, что фотон претерпит отражение в точке М и придет в другую точку на лабораторной стене, а именно в точку В на рис. 8.3. Возводя соответствующие амплитуды в квадрат, мы снова получаем для обеих вероятностей значения, равные одной второй. Следует, однако, отдавать себе отчет в том, на какие именно вопросы отвечают эти вероятности. А вопросы следующие: «Если известно, что лампа L сработала, то какова вероятность срабатывания фотоэлемента Р?» — тот же самый вопрос, что мы рассматривали до этого; и более экстравагантный вопрос: «Какова вероятность срабатывания фотоэлемента Р при условии, что известен факт испускания фотона из стены в точке В?»
Мы можем рассматривать оба ответа как экспериментально «правильные» в определенном смысле, хотя второй ответ (испускание фотона из стены) скорее представляет собой логическое умозаключение, а не результат реально выполненного ряда экспериментов! Однако ни один из этих вопросов не является обращением во времени того, что был задан выше. Обращенный вспять во времени вопрос звучал бы так:
«Если известно, что фотоэлемент Р сработал, то какова вероятность того, что сработала лампа L?»
Отметим, что правильный экспериментальный ответ на этот вопрос — это никакая не «одна вторая», а
«единица».
В случае срабатывания фотоэлемента нет практически никаких сомнений в том, что фотон пришел от лампы, а не от лабораторной стены! На наш обращенный во времени вопрос проведенный в рамках квантовой механики расчет дал нам абсолютно неверный ответ!
Отсюда следует, что правила R-части квантовой механики просто-напросто неприменимы к такого рода обращенным во времени задачам. Если мы хотим рассчитать вероятность прошлого состояния исходя из известного состояния в будущем, то применение стандартной R-процедуры, которая заключается в простом возведении в квадрат модуля квантово-механической амплитуды, приводит к неверным результатам. Эта процедура пригодна только для расчета вероятностей будущих событий исходя из прошлых событий — и в этом случае она работает великолепно! Поэтому я считаю совершенно очевидным, что R-процедура не может быть симметрична во времени (и, между прочим, вследствие этого не выводима из симметричной во времени процедуры U).
Многие могут посчитать, что причина этого противоречия с временно?й симметрией состоит в том, что второму началу термодинамики каким-то образом все же удалось пролезть в цепь рассуждений и привнести дополнительную асимметрию во времени, не описываемую процедурой возведения амплитуды в квадрат. Действительно, кажется, что любой физический измерительный прибор, способный реализовать R-процедуру, должен содержать элемент «термодинамической необратимости» — так, что энтропия возрастает всякий раз, когда имеет место измерение. Я думаю, что процесс измерения должен быть фундаментальным образом связан со вторым началом термодинамики. Более того, по-видимому попытки обратить вспять во времени целиком весь процесс квантово-механического эксперимента, вроде описанного выше (идеализированного) опыта, с регистрацией всех проведенных измерений, бессмысленны. Я не задавался вопросом о том, как далеко мы можем пойти по пути действительного обращения эксперимента во времени. Меня интересовала только применимость этой замечательной квантово-механической процедуры, которая дает правильные вероятности через вычисление квадратов модулей амплитуд. Поразительно, что эта простая процедура применима в направлении от прошлого к будущему и при этом не требует никакой дополнительной информации о системе. Действительно, невозможность повлиять на эти вероятности, которые в квантовой теории являются абсолютно случайными, представляет собой одну из неотъемлемых частей рассматриваемой теории! Однако попытка применить те же самые процедуры в направлении от будущего к прошлому (т. е. не для предсказания будущего, а для установления прошлого) приводит к результату неверному до удивления. Можно приводить сколько угодно оправданий, смягчающих обстоятельств и других доводов для объяснения того, почему процедура возведения амплитуды в квадрат не дает правильных результатов в случае применения ее в направлении от будущего к прошлому, но факт остается фактом. А при рассмотрении ситуации от прошлого к будущему никакие оправдания попросту не нужны! Процедура R, в том виде, как она реально применяется, просто-напросто не является симметричной во времени.
- Временная шкала
- Преждевременная точность
- 15.5.3. Современная lint
- 1. Современная типология выставок
- Вектора, допускающие сложение
- 6.16.6 Временная метка
- 7.6.3 Временная метка и ответ на Timestamp
- 8.4.1 Протоколы вектора расстояния
- 16.7 Временная метка и идентификатор сообщения
- Совет 23. Рассмотрите возможность замены ассоциативных контейнеров сортированными векторами
- Современная криптография
- Симметрия и асимметрия




