Книга: Новый ум короля: О компьютерах, мышлении и законах физики
Когда происходит редукция вектора-состояния?
Когда происходит редукция вектора-состояния?
Предположим, что мы признаем, исходя из вышеизложенных соображений, что редукция вектора-состояния может каким-то образом оказаться гравитационным феноменом. Можно ли сформулировать связь между R-процедурой и гравитацией более явным образом? Когда, согласно этой концепции, должен фактически иметь место коллапс вектора состояния?
Здесь следует прежде всего отметить, что даже в рамках более «традиционных» подходов к построению квантовой теории гравитации согласование принципов обшей теории относительности с правилами квантовой механики наталкивается на определенные и весьма серьезные технические трудности. Эти правила (в первую очередь — интерпретация импульсов как дифференцирования по координатам в уравнении Шредингера — см. гл.7 «Космология и Большой взрыв») плохо вписываются в представление об искривленной геометрии пространства-времени. Я лично считаю, что введение «значительной» пространственно-временно?й кривизны влечет неизбежное нарушение правил квантовой линейной суперпозиции. Именно в этом случае суперпозиция комплексных амплитуд в принципе допустимых альтернатив заменяется набором вероятностно-взвешенных реальных альтернатив, из которых одна фактически имеет место.
Что я понимаю здесь под «значительной» степенью кривизны? Я имею в виду достижение такой степени кривизны, при которой ее характерное значение становится сравнимым с одногравитонным [195] масштабом или превышает его. (Напомним, что, согласно правилам квантовой теории, электромагнитное поле «квантуется» на отдельные элементы, называемые «фотонами». При разложении поля на его частотные составляющие, компонента с частотой v может входить в это разложение только в виде целого числа фотонов, каждый с энергией равной hv. Предполагается, что аналогичные правила должны быть также применимы и к гравитационному полю.) Один гравитон — это минимальная единица кривизны, допускаемая квантовой теорией. Идея состоит в том, что при достижении этого уровня обычные правила линейной суперпозиции, предписываемые процедурой U, должны претерпеть определенные изменения при их применении к гравитонам, и при этом возникает некая асимметричная во времени «нелинейная неустойчивость». Мы получаем вместо комплексных суперпозиций неограниченно долго сосуществующих «альтернативных возможностей» ситуацию, когда одна из «возможностей» начинает на этом этапе одерживать верх над другими и система «перескакивает» в то или иное из альтернативных состояний. Возможно, что выбор одного из альтернативных состояний происходит случайно, а быть может, в его основе лежат какие-то более глубокие законы. Однако теперь реальность обретает вид одного из альтернативных состояний. Процедура R осуществилась.
Отметим, что согласно этой гипотезе R-процедура осуществляется спонтанно, совершенно объективно и независимо от какого бы то ни было вмешательства человека. Идея состоит в том, что «одногравитонный уровень» должен находиться как раз между «квантовым уровнем» атомов, молекул и т. д., на котором хорошо действуют линейные правила (U) обычной квантовой механики, и «классическим уровнем» нашего повседневного опыта. Насколько «велик» одногравитонный уровень? Отметим, что дело тут на самом деле не в физическом размере, а скорее в распределении массы и энергии. Как мы видели, эффекты квантовой интерференции могут возникать и на больших расстояниях при условии, что связанная с ними энергия мала. (Вспомним самоинтерференцию фотона, описанную на в гл. 6 «Одна частица — сразу в двух местах?», и эксперименты типа ЭПР, проведенные Клаузером и Аспектом, гл.6 «Эксперименты с фотонами: проблема для специальной теории относительности?»). Характерный масштаб массы в квантовой гравитации известен под названием планковской массы, приблизительно равной
mPl = 10 -5 г.
Она может показаться гораздо большей, чем хотелось бы, поскольку в простых наблюдениях мы видим, как гораздо менее массивные объекты, например, пылинки, ведут себя классическим образом. (Величина mPl немного меньше массы блохи.) Однако, я не думаю, что одногравитонный критерий применим столь грубым образом. Я постараюсь высказываться по возможности яснее, но на момент написания этих строк вопрос о конкретном способе применения рассматриваемого критерия остается в значительной степени открытым.
Давайте рассмотрим сначала очень непосредственный способ наблюдения частицы — при помощи камеры Вильсона. В этом случае мы имеем камеру, заполненную паром, находящимся на грани конденсации в капельки воды. При попадании в такую камеру быстро движущейся частицы — например, частицы, возникшей в результате распада расположенного вне камеры радиоактивного атома, ее прохождение сквозь камеру вызывает ионизацию расположенных вблизи траектории пролета атомов (т. е. атомы становятся заряженными в результате отрыва от них электронов). Эти ионизированные атомы служат центрами конденсации капелек из водяного пара. Таким образом возникает трек, состоящий из капелек, которые могут непосредственно наблюдаться экспериментатором (рис. 8.7).
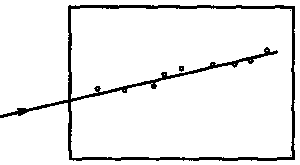
Рис. 8.7. Заряженная частица влетает в камеру Вильсона и вызывает конденсацию капелек на своем пути
Ну а как же все это описывается в квантовой механике? В момент распада радиоактивного атома он испускает частицу. Но у этой частицы существует множество различных направлений движения: каждое направление движения описывается своей амплитудой, причем все они сосуществуют одновременно в виде линейной квантовой суперпозиции. Совокупность всех этих наложенных друг на друга альтернатив образует исходящую из распавшегося атома сферическую волну — волновую функцию испущенной атомом частицы. При попадании любого из возможных треков частицы в камеру, он тут же оказывается ассоциированным с цепочкой ионизованных атомов, каждый из которых служит центром конденсации пара. Все эти различные возможные цепочки ионизованных атомов должны сосуществовать в виде линейной квантовой суперпозиции, так что мы имеем теперь линейную суперпозицию большого числа различных цепочек конденсирующихся капелек. На некотором этапе эта комплексная квантовая линейная суперпозиция превращается в действительную совокупность фактических альтернатив с вероятностными весами, равными, согласно R-процедуре, квадратам модулей амплитуд вероятностей. В реальном физическом мире реализуется только одна из этих альтернатив, и именно она наблюдается экспериментатором. В соответствии с излагаемой здесь точкой зрения эта стадия наступает, когда разность между гравитационными полями различных альтернативных вариантов достигает одногравитонного уровня.
Когда это происходит? Согласно очень грубым расчетам[196], если бы имелась только одна однородная шарообразная капля, то одногравитонный уровень достигался бы, когда ее масса вырастет до одной сотой от величины mPl, что составляет одну десятимиллионную грамма. В этом расчете много неопределенностей (включая трудности принципиального характера), да и величина полученной массы несколько великовата, однако результат не совсем уж бессмысленный. Остается надеяться на появление в будущем более точных расчетов и возможность рассмотрения всей цепочки, а не просто одной из составляющих ее капель. К тому же учет неоднородности капель — того факта, что они состоят из большого числа мельчайших атомов, может существенно изменить результат, да к тому же сам «одногравитонный критерий» нуждается в существенном математическом уточнении.
В описанной выше ситуации рассматривалось возможное реальное наблюдение квантового процесса (распада радиоактивного атома), при котором квантовые эффекты оказываются усиленными настолько, что различные квантово-механические альтернативы приводят к различным и непосредственно наблюдаемым макроскопическим альтернативам. Я считаю, что R-процедура действительно может иметь место объективным образом даже в отсутствие столь ярко выраженного усиления. Предположим, что наша частица попала не в камеру Вильсона, а просто в большой ящик, заполненный газом (или жидкостью) с плотностью, обеспечивающей практически гарантированное столкновение частицы или иное ее воздействие на большое число атомов газа. Рассмотрим всего два варианта возможного поведения частицы, как составные части начальной линейной суперпозиции: частица может просто не попасть в ящик совсем или же она попадет в него по определенной траектории и окажется отраженной каким-либо атомом газа. Во втором случае соответствующий атом газа отскочит, двигаясь с очень большой скоростью так, как он никогда не повел бы себя, не столкнись он с частицей, затем столкнется с еще одним атомом и, в свою очередь, отрикошетит от него. После этого движение двух атомов будет отличаться от их движения в отсутствие столкновения с частицей, и мы будем иметь уже целый каскад движений атомов в газе, невозможный в отсутствие первоначального попадания частицы в ящик (рис. 8.8).
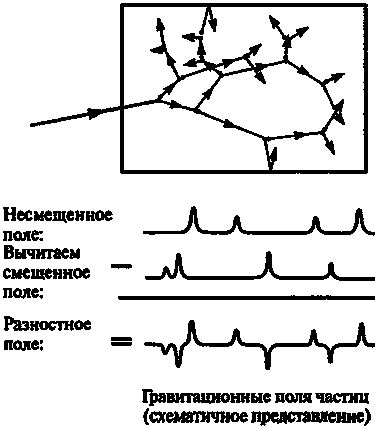
Рис. 8.8. Гравитационные поля частиц (условное
изображение). При попадании частицы в ящик с газом через некоторое время практически все атомы газа оказываются охваченными порожденным частицей возмущением. Линейная квантовая суперпозиция частицы, попавшей в ящик, и частицы, не попавшей в ящик, подразумевает линейную суперпозицию двух различных пространственно-временных геометрий, описывающих гравитационные поля двух различных распределений частиц газа. В какой момент различие между этими геометриями достигает одногравитонного уровня?
Вскоре после этого порожденное частицей возмущение охватит практически все атомы газа.
Подумаем теперь, как эту ситуацию можно описать на языке квантовой механики. Вначале мы имеем лишь исходную частицу, и ее различные положения составляют комплексную линейную суперпозицию — волновую функцию частицы. Однако через какое-то время квантово-механическое описание должно уже охватывать все атомы газа. Рассмотрим комплексную суперпозицию двух возможных траекторий частицы, при движении по одной из которых частица попадает в ящик, а по другой — нет. Стандартная квантовая механика требует распространения этой суперпозиции на все атомы газа: мы должны рассмотреть суперпозицию двух состояний, таких, что положение атомов газа в одном состоянии оказываются смещенными относительно их положений в другом состоянии. Теперь рассмотрим разность гравитационных полей всех отдельных атомов. Хотя распределение газа (и гравитационное поле) в целом практически одинаково для обоих состояний, чью суперпозицию мы должны рассмотреть, если мы вычтем одно поле из другого, то получим (сильно флуктуирующее) разностное поле, которое вполне может оказаться «значительным» в подразумеваемом здесь смысле — а именно это разностное поле вполне может превысить одногравитонный уровень. По достижении этого уровня немедленно же происходит редукция вектора состояния: в реальном состоянии частица либо попала в ящик, либо нет. Комплексная линейная суперпозиция сводится к статистически взвешенным альтернативам с осуществлением только одной из них.
В предыдущем примере я рассматривал камеру Вильсона в качестве способа квантово-механического наблюдения. Я считаю, что и другие виды таких наблюдений (фотопластинки, искровые камеры и т. д.) можно анализировать в рамках одногравитонного критерия, используя подход, примененный в описанном выше случае ящика с газом. Многое еще предстоит сделать, чтобы разобраться в подробностях применения этой процедуры.
Изложенные здесь соображения представляют собой всего лишь зачаток новой теории, которая, как мне кажется, является столь необходимой[197]. Для того, чтобы быть полностью удовлетворительной, любая схема должна, по-моему, включать в себя радикально обновленные представления о природе пространственно-временно?й геометрии, быть может, с применением нелокального описания[198]. Один из самых неоспоримых доводов в пользу этого следует из экспериментов ЭПР-типа (см. гл.6 «„Парадокс“ Эйнштейна, Подольского и Розена» и гл.6 «Эксперименты с фотонами: проблема для специальной теории относительности?»), в которых «наблюдение» (в данном случае — срабатывание фотоэлемента) в одном конце комнаты может вызвать мгновенную редукцию вектора-состояния в другом конце комнаты. Построение полностью объективной теории редукции вектора-состояния, не противоречащей духу теории относительности, представляет собой очень трудную и глубокую задачу, поскольку понятие «одновременности», будучи зависимым от движения некоторого наблюдателя, является чуждым теории относительности. Я убежден, что наше современное представление о физической реальности — особенно в том, что касается природы времени — нуждается в коренном пересмотре, пожалуй, даже в более радикальном, чем тот, который был вызван к жизни современной теорией относительности и квантовой механикой.
Вернемся к исходной проблеме. Какое все это имеет отношение к физическим законам, которые управляют действиями нашего мозга? Как это связано с нашими мыслями и чувствами? Для того, чтобы попытаться хоть как-то ответить на эти вопросы, придется сначала немного разобраться в устройстве нашего мозга. Потом я вернусь к проблеме, которую считаю фундаментальной: какого рода новые физические действия происходят, когда мы сознательно мыслим или воспринимаем что-либо?
- Когда нужен постскриптум в бизнес-тексте?
- Как я нашла «правильных» потребителей, когда искала «неправильных»
- Когда старая школа молода
- Что происходит, когда бренды растут или идут на спад
- Пример 9-8. Содержимое $* и $@, когда переменная $IFS -- пуста
- Когда следует задавать проясняющие вопросы
- Когда печатаю, перед повтором буквы приходится выжидать несколько секунд
- Когда я не работаю за компьютером, через некоторое время он отключается. Можно ли это исправить?
- Наносится ли какой-нибудь вред USB-брелоку, когда его извлекают из разъема без использования функции безопасного отключе...
- Как узнать, когда сеть подключена, а когда нет? У меня плохой разъем на сетевой карте, и связь иногда пропадает
- Когда включаю компьютер, при загрузке пишется Insert system disk and press enter. Что нужно делать?
- Когда звонит телефон, начинает загружаться компьютер. Помогает только отключение кабеля от модема. Почему так происходит...




