Книга: Основы объектно-ориентированного программирования

Вектора, допускающие сложение

Вектора, допускающие сложение

Приведем простой, но характерный пример, демонстрирующий необходимость введения ограниченной универсальности. Он поможет в обосновании метода решения поставленной задачи и в выборе соответствующей конструкции языка.

Предположим, что мы хотим объявить класс VECTOR, над элементами которого определена операция сложения. Потребность в подобном базовом классе неоспорима. Вот первый вариант:

indexing
description: "Векторы со сложением"
class
VECTOR [G]
feature -- Доступ
count: INTEGER
-- Количество элементов
item, infix "@" (i: INTEGER): G is
-- Элемент вектора с индексом i (нумерация с 1)
require ... do
...
end
feature -- Основные операции
infix "+" (other: VECTOR [G]): VECTOR is
-- Поэлементное сложение текущего вектора с other
require ... do
...
end
... Прочие компоненты ...
invariant
non_negative_count: count >= 0
end

Применение инфиксной записи продиктовано соображениями удобства. Для удобства введены и синонимы в обозначении i-го компонента вектора: v.item (i) или просто v @ i.

Обратимся к функции "+". Сначала сложение двух векторов кажется очевидным и состоящим в суммировании элементов на соответствующих местах. Общая его схема такова:

infix "+" (other: VECTOR [G]): VECTOR is
-- Поэлементное сложение текущего вектора с other
require
count = other.count
local
i: INTEGER
do
"Создать Result как массив из count элементов"
from i := 1 until i > count loop
Result.put(item (i) + other.item (i), i)
i := i + 1
end
end

Выражение в прямоугольнике - результат сложения i-го элемента текущего вектора с i-м элементом other. Процедура put сохраняет это значение в i-м элементе Result, и хотя она не показана в классе VECTOR, данная процедура в нем, безусловно, присутствует.

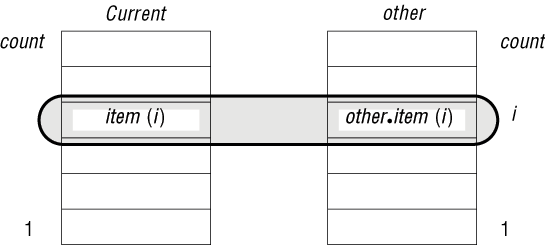
Рис. 16.5.  Поэлементное сложение векторов

Но подобная схема не работает! Операция +, которую мы определили для сложения векторов (VECTOR), здесь применяется к объектам совсем другого типа (G), являющегося родовым параметром. По определению, родовой параметр представлен неизвестным типом - фактическим параметром, появляющимся только тогда, когда нам понадобится для каких либо целей родовой класс. Процесс порождения класса при задании фактического родового параметра называется родовым порождением (generic derivation). Если фактическим параметром служит INTEGER либо иной тип (класс), содержащий функцию infix "+" правильной сигнатуры, корректная работа обеспечена. Но что если параметром станет ELLIPSE, STACK, EMPLOYEE или другой тип без операции сложения?

С прежними родовыми классами: контейнерами STACK, LIST и ARRAY - этой проблемы не возникало, поскольку их действия над элементами (типа G как формального параметра) были универсальны - операции (присваивание, сравнение) могли выполняться над элементами любого класса. Но для абстракций, подобных векторам, допускающих сложение, нужно ограничить круг допустимых фактических родовых параметров, чтобы быть уверенными в допустимости проектируемых операций.

Этот случай отнюдь не является исключением. Вот еще два примера того же рода.

[x]. Предположим, вы проектируете класс, описывающий структуру данных с операцией sort, упорядочивающей элементы структуры в соответствии с некоторым критерием сортировки. Тогда элементы этой структуры должны принадлежать типу, для которого определена операция сравнения infix "<=", задающая порядок для любой пары соответствующих объектов.

[x]. При разработке таких базисных структур данных как словари зачастую используется для хранения данных хеш-таблица, в которой место элемента определяется ключом, вычисляемым по значению элемента. Элементы, размещаемые в словаре должны принадлежать классу, допускающему применение хеш-функции, вычисляющей ключ каждого элемента.

Оглавление книги