Книга: Новый ум короля: О компьютерах, мышлении и законах физики
«Плиточные» структуры и квазикристаллы
«Плиточные» структуры и квазикристаллы
Теперь я отойду от масштабных обсуждений последних нескольких разделов и сосредоточусь на обсуждении вопросов, которые, хотя и являются до некоторой степени дискуссионными, все же гораздо более научны и «осязаемы». Возможно, вначале эти рассуждения покажутся отклонением от темы, однако, их важность для нас станет очевидной уже в следующем разделе.
Вспомним примеры «плиточных» замощений, изображенные на рис. 4.12 (гл.4 «Некоторые примеры нерекурсивной математики»). Эти образцы интересны потому, что они «почти» нарушают общепринятую математическую теорему о кристаллических решетках, которая утверждает, что для кристаллических решеток возможны только симметрии с осью второго, третьего, четвертого и шестого порядков. Под кристаллической решеткой я подразумеваю дискретную систему точек, которая обладает трансляционной симметрией. Это означает, что можно определенным образом перемещать решетку без вращения так, чтобы она переходила сама в себя (иными словами, в результате такого сдвига она не изменяется) — а, значит, у такой решетки будет существовать параллелограмм периодов (см. рис. 4.8). Примеры «плиточных» замощений с этими разрешенными теорией типами вращательной симметрии показаны на рис. 10.2.
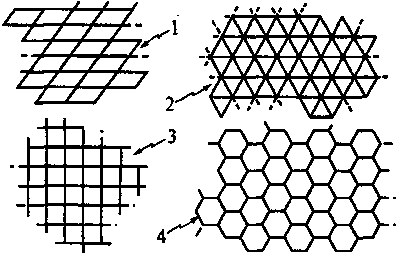
Рис. 10.2. Периодические плиточные замощения с разными типами симметрии (где в каждом случае центр симметрии совпадает с центром плитки): 1) с осью второго порядка; 2) с осью третьего порядка; 3) с осью четвертого порядка; 4) с осью шестого порядка
С другой стороны, покрытия на рис. 4.12, как и изображенные на рис. 10.3

Рис. 10.3. Квазипериодическая плиточная структура (следует заметить, что она образована посредством объединения образцов с рис. 4.11) с кристаллографически «невозможной» квазисимметрией с осью пятого порядка
(которые, в сущности, представляют собой замощения, образованные соединением решеток, изображенных на рис. 4.11 (гл.4 «Некоторые примеры нерекурсивной математики»), почти имеют трансляционную симметрию и почти обладают симметрией вращения с осью пятого порядка, где «почти» означает, что можно найти такие движения решеток (соответственно, трансляционные и вращательные), при которых решетка переходит сама в себя с любой наперед заданной точностью (кроме 100 %-ной). Не стоит углубляться, что точно означает это утверждение. Единственное, что нам здесь важно — это если в нашем распоряжении есть вещество, в котором все атомы расположены в узлах кристаллической решетки с подобной структурой, то оно будет выглядеть, как кристалл, обладая при этом запрещенной симметрией с осью пятого порядка!
В декабре 1984 году израильский физик Дэни Шехтман, работавший вместе с коллегами в Национальном бюро стандартов в США, в Вашингтоне, объявил об открытии фазы алюминиево-марганцевого сплава, который был похож на кристаллоподобное вещество — теперь называемое квазикристаллом — с осью пятого порядка. На самом деле, у этого квазикристаллического вещества наблюдалась симметрия не только на плоскости, но и в трех измерениях — так что в итоге получалась запрещенная икосаэдральная симметрия (Шехтман и др. [1984]). (Икосаэдральный трехмерный аналог моей плоской «плиточной» структуры с осью пятого порядка был открыт Робертом Амманном в 1975 году; см. Гарднер [1989].) Сплавы Шехтмана образовывали только крошечные микроскопические квазикристаллы, достигавшие примерно 10 -3 мм в поперечном сечении, но позднее были найдены другие квазикристаллические вещества, в частности — алюминиево-литиево-медный сплав, у которого икосаэдрально симметричные образования могут вырастать до размеров порядка миллиметра, т. е. становятся вполне различимы невооруженным глазом (рис. 10.4).
Рис. 10.4. Квазикристалл (сплав AL—Li—Сu) с, казалось бы, невозможной кристаллической симметрией. (Из Гэйл [1987].)
Замечательным свойством этих квазикристаллических «плиточных» структур является то, что процесс их составления имеет существенно нелокальный характер. Иными словами: при построении подобного покрытия необходимо время от времени проверять состояние кристаллической решетки на расстоянии многих и многих «атомов» от места сборки, чтобы избежать серьезных ошибок при соединении составных частей. (Это чем-то напоминает то почти «сознательное нащупывание», которое я связывал с естественным отбором.) Наличие такого свойства является одной из причин серьезных разногласий, возникающих сегодня в связи с вопросом о квазикристаллических структурах и их выращивании, так что было бы неразумно пытаться делать окончательные выводы до тех пор, пока не будут разрешены некоторые основополагающие проблемы. Тем не менее, никто не запрещает нам выдвигать предположения; поэтому я рискну высказать здесь свою собственную точку зрения. Во-первых, я полагаю, что некоторые из этих квазикристаллических веществ действительно имеют сложное внутреннее строение, и что расположение атомов в их структуре довольно точно повторяет строение тех плиточных структур, которыми я занимался. Во-вторых, отсюда я делаю (всего лишь гипотетическое) заключение о том, что их образование не может совершаться за счет последовательного добавления атомов, как это происходит в рамках классической картины роста кристаллов — но с необходимостью должна опираться на нелокальные и непременно квантово-механические принципы построения[224].
Механизм такого роста я представляю себе следующим образом: вместо присоединения отдельных атомов к постоянно движущейся линии роста (в случае классического роста кристаллов), происходит квантовая линейная суперпозиция большого числа различных альтернативных сочетаний присоединяющихся атомов (путем квантовой операции U). В самом деле, согласно квантовой механике, все именно так и должно (почти всегда) происходить! В каждый момент времени существует не одна возможная структура, но множество альтернативных расположений атомов в сложной линейной суперпозиции. Некоторые из этих структур вырастают в гораздо более крупные образования, так что в определенный момент различия между гравитационными полями альтернативных структур превзойдут «одногравитонный предел» (или его более подходящий в данном случае аналог; см. главу 8, «Когда происходит редукция вектора-состояния?»). На этой стадии одна из них — или, скорее, это снова будет суперпозиция, но уже в несколько урезанном виде — выделиться в качестве истинной структуры (квантовая операцияR). В этот процесс роста, сопровождающийся последовательным отказом от наименее «значимых» на каждом этапе альтернатив, будут вовлекаться все бо?льшее и бо?льшее количество исходного вещества, пока наконец не сформируется достаточно крупный квазикристалл.
Обычно, когда природа ищет кристаллическую конфигурацию, из всех возможных она выбирает ту, которая характеризуется наименьшим уровнем энергии (считая фоновую температуру нулевой). Нечто аналогичное, по-моему, должно происходить и в процессе роста кристаллов, с той только разницей, что такое состояние с наименьшей энергией гораздо труднее обнаружить, а «наилучшее» расположение атомов не может быть получено просто последовательным добавлением каждый раз одного атома в надежде на то, что индивидуальному атому для этого будет достаточно решить свою собственную задачу минимизации. Вместо этого нам предстоит решать эту же задачу для всей совокупности атомов, а значит, потребуется их совместное усилие. Такое взаимодействие, в моем представлении, должно иметь квантово-механическую природу; и достигаться оно должно при помощи множества различных комбинаций атомных структур, которые одновременно «проверяются» в линейной суперпозиции (примерно так же, как это, вероятно, происходит в квантовом компьютере, упомянутом в конце главы 9).
Условием для выбора подходящего (хотя, возможно, не лучшего) решения задачи минимизации должно быть выполнение «одногравитонного критерия» (или приемлемой в данном конкретном случае альтернативы), что, предположительно, имеет место только при соответствующих физических условиях.
- Для чего нужны умы?
- Что в действительности делает сознание?
- Естественный отбор алгоритмов?
- Неалгоритмическая природа математической интуиции
- Вдохновение, озарение и оригинальность
- Невербальность мысли
- Сознание у животных?
- Соприкосновение с миром Платона
- Взгляд на физическую реальность
- Детерминизм и жесткий детерминизм
- Антропный принцип
- «Плиточные» структуры и квазикристаллы
- Возможная связь с пластичностью мозга
- Временны?е задержки в реакции сознания
- Странная роль времени в сознательном восприятии
- Заключение: точка зрения ребенка
- 1.4 Структуры данных, связанные с драйверами устройств Windows
- ВЛОЖЕННЫЕ СТРУКТУРЫ
- Практическая работа 35. Создание структуры документа и вставка оглавления
- Разработка структуры базы данных
- 6.2. Типы и структуры данных
- Ветвящиеся структуры – архитектура мира растений
- Построение структуры веб-страницы
- Фундаментальные алгоритмы и структуры данных в Delphi
- 4.2. Представление базовой структуры программы
- 14. Структуры и другие типы данных
- Структуры данных процесса
- Структуры данных




