Книга: Основы объектно-ориентированного программирования

Инварианты реализации

Инварианты реализации

Некоторые утверждения появляются в реализации, хотя они не имеют прямых двойников в спецификации АТД. Эти утверждения используют атрибуты, включая некоторые закрытые атрибуты, которые, по определению, не имеют смысла в АТД. Простым примером являются свойства, появляющиеся в инварианте STACK4:

count_non_negative: 0 <= count
count_bounded: count <= capacity

Такие утверждения составляют часть инварианта класса, известную как инвариант реализации (implementation invariant). Они позволяют задать соответствие представления реализации, выбранное в классе, (здесь это атрибуты count, capacity, representation) - визави соответствующего АТД.

Рис. 11.5 помогает понять концепцию инварианта реализации. Он иллюстрирует характеристические свойства функции абстракции, представленной вертикальной стрелкой на рисунке. Об этом стоит поговорить подробнее.

Прежде всего, корректно ли рассматривать а, как функцию? Напомним, что функция (тотальная или частичная) отображает каждый элемент исходного множества ровно в один элемент целевого множества, в противоположность общему случаю отношения, не имеющего такого ограничения. Рассмотрим обратное преобразование (сверху - вниз) от абстрактного объекта к конкретному. Будем называть его отношением представления (representation relation); как правило, это отношение не является функцией, так как существует множество представлений одного и того же абстрактного объекта. В реализации стека массивом, где каждый стек задан парой <representation, count>, абстрактный стек имеет много различных представлений, иллюстрируемых следующим рис. 11.6. Все они имеют одно и то же значение count и одинаковые элементы массива representation для всех индексов в пределах от 1 до count, но размер массивов - capacity - может быть любым значением, большим или равным count; элементы массива с индексом, большим count могут содержать произвольные значения.

Так как интерфейс класса ограничен компонентами, непосредственно выводимыми из функций АТД, клиенты не имеют способа различать поведение конкретных объектов, представляющих один и тот же абстрактный стек (это и есть причина, по которой все они имеют одну функцию абстракции a). Заметьте, в частности, что процедура remove из STACK4 выполняет свою работу, просто изменяя count

count := count - 1

не пытаясь очистить выше расположенные элементы. Всякое изменение элементов, расположенных выше count, будет модифицировать конкретный стек CS, не оказывая никакого влияния на ассоциированный абстрактный стек a(CS).

Итак, отношение реализации это обычно не функция. Но инверсия этого отношения - функция абстракции - действительно является функцией, так как каждому конкретному объекту ставится в соответствие один абстрактный объект. В примере стека каждой правильной паре <representation, count> соответствует в точности один абстрактный стек. У него count элементов, растет снизу вверх, элементы representation имеют индексы в пределах от 1 до count.

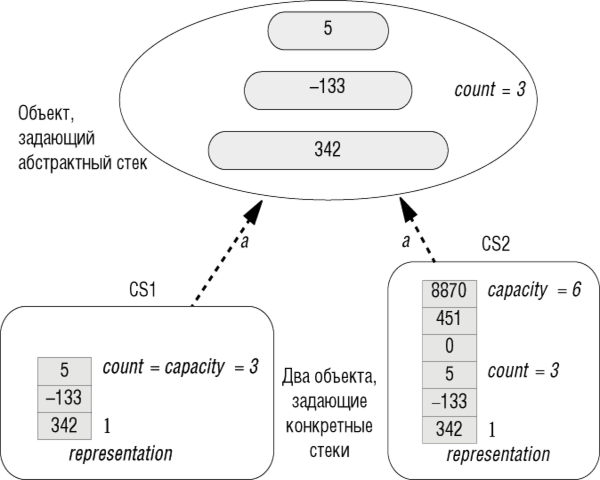
Рис. 11.6.  Один абстрактный объект и два его представления

Оба конкретных стека, изображенные на рисунке, являются реализациями абстрактного стека, состоящего из трех элементов со значениями: 342, -133, 5. Отображение а должно быть функцией, иначе конкретный объект мог быть интерпретирован как реализация двух или более различных абстракций. В этом случае выбранная реализация двусмысленна и, следовательно, неадекватна. Поэтому стрелка, ассоциированная с а, правильно отображает существующую функциональную зависимость между абстрактными и конкретными типами. (Обсуждение наследования будет делаться при тех же предположениях).

Функция абстракции а обычно представима частичной функцией: не для каждого возможного конкретного объекта существует правильное представление абстрактного объекта. Например, не каждая пара <representation, count> является правильным представлением абстрактного стека. Если representation является массивом емкости 3 и count = 4, то они совместно не представляют абстрактный стек. Правильные представления (члены, входящие в область определения функции абстракции), - только те пары, для которых count находится между 0 и размерностью массива. Это свойство является инвариантом реализации.

В математических терминах, инвариант реализации является характеристической функцией области определения абстрактной функции. Другими словами, это булево свойство, определяющее применимость функции. (Характеристическая функция подмножества А задает булево свойство, истинное на А и ложное всюду вне его.)

Инвариант реализации является той частью утверждений класса, у которой нет двойника в спецификации АТД. Он не связан с АТД, и относится только к реализации. Он определяет, при каких условиях кандидат - конкретный объект - действительно является реализацией одного и только одного абстрактного объекта.

Оглавление книги