Книга: Основы объектно-ориентированного программирования

Инварианты и варианты цикла

Наши следующие и последние конструкции утверждений помогут строить корректные циклы. Эти конструкции являются прекрасным дополнением рассмотренных ранее механизмов. Поскольку они не являются специфической частью ОО-метода, то вы вправе пропустить этот раздел при первом чтении.

Трудности циклов

Возможность повторять некоторые вычисления произвольное число раз, не поддаваясь усталости, без случайных потерь чего-либо важного, - в этом принципиальное отличие компьютерных вычислений от возможностей человека. Вот почему циклы так важны. Трудно вообразить, что можно было бы делать в языках, в которых были бы только две управляющие структуры - последовательность и выбор, - но не было бы циклов и не было бы поддержки рекурсии, еще одного базисного механизма поддержки итеративных вычислений.

Но с мощностью приходят и риски. У циклов дурная слава, - их трудно заставить работать правильно. Типичными для циклов являются:

[x]. Ошибки "больше-меньше" (выполнение цикла слишком много или слишком мало раз).

[x]. Ошибки управления пограничными ситуациями, например пустыми структурами. Цикл может правильно работать на больших массивах, но давать ошибки, когда у массива один элемент или он вообще пуст.

[x]. Ошибки завершения ("зацикливание") в некоторых ситуациях.

Бинарный поиск - один из ключевых элементов базового курса "Введение в информатику" (Computer Science 101) - хорошая иллюстрация "коварства" циклов даже в относительно тривиальной ситуации. Рассмотрим целочисленный, упорядоченный по возрастанию массив t с индексами от 1 до n. Используем алгоритм бинарного поиска для ответа на вопрос: появляется ли целое x среди элементов массива. Если массив пуст, ответ должен быть "нет", если в массиве ровно один элемент, то ответ "да" тогда и только тогда, когда элемент массива совпадает с x. Суть бинарного поиска, использующего упорядоченность массива, проста: вначале x сравнивается со средним элементом массива, если есть совпадение, то задача решена, если x меньше среднего элемента, то поиск продолжается в верхней половине массива, в противном случае - в нижней половине. Каждое сравнение уменьшает размер массива вдвое. Ниже представлены четыре попытки реализации этой простой идеи. К несчастью, все они содержат ошибки. Вам предоставляется случай поупражняться в поиске ошибок и установить, в какой ситуации каждый из алгоритмов не работает нужным образом.

Таблица 11.3.Четыре (ошибочных) попытки реализации бинарного поиска

Сделаем циклы корректными

Разумное использование утверждений может помочь справиться с такими проблемами. Цикл может иметь связанное с ним утверждение, так называемый инвариант цикла (loop invariant), который не следует путать с инвариантом класса. Он может также иметь вариант цикла (loop variant), являющийся не утверждением, а, обычно целочисленным выражением. Совместно, инвариант и вариант позволяют гарантировать корректность цикла.

Для понимания этих понятий необходимо осознать, что цикл - это способ вычислить некоторый результат последовательными приближениями (successive approximations).

Рассмотрим тривиальный пример вычисления максимума в целочисленном массиве, используя очевидный алгоритм:

maxarray (t: ARRAY [INTEGER]): INTEGER is
-- Максимальное значение массива t
require
t.capacity >= 1
local
i: INTEGER
do
from
i := t.lower
Result := t @ lower
until i = t.upper loop
i := i + 1
Result := Result.max (t @ i)
end
end

В разделе инициализации i получает значение нижней границы массива, а сущность Result - будущий результат вычислений - значение первого элемента. Предусловие гарантирует существование хотя бы одного элемента в массиве. Производя последовательные итерации в цикле, мы достигаем верхней границы массива, увеличивая на каждом шаге i на 1, и заменяя Result значением элемента t @ i, если этот элемент больше чем Result. Для нахождения максимума двух целых используется функция max, определенная для класса integer: a.max(b) возвращает максимальное значение из a и b.

Это пример вычисления последовательными приближениями. Мы продвигаемся вверх по массиву последовательными нарезками: [lower, lower], [lower, lower+1], [lower, lower+2] и так вплоть до полного приближения [lower, upper].

Свойство инварианта цикла состоит в том, что на каждом шаге прохождения цикла Result представляет максимум текущей нарезки массива. Инициализация гарантирует выполнимость этого свойства непосредственно перед началом работы цикла. Каждая итерация увеличивает нарезку, сохраняя истинность инварианта. Цикл завершает свою работу, когда очередная нарезка массива совпадает со всем массивом. В этом состоянии истинность инварианта означает, что Result является максимумом массива, что и является требуемым результатом работы.

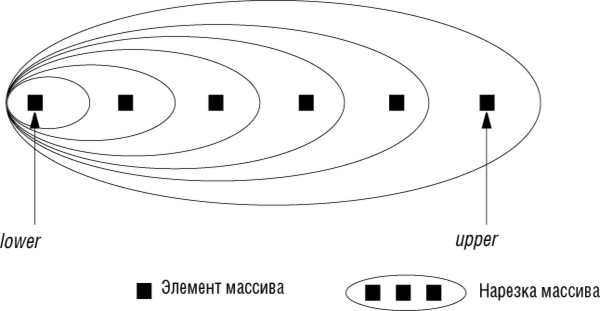
Рис. 11.7.  Аппроксимация массива последовательными нарезками

Ингредиенты доказательства корректности цикла

Простой пример вычисления максимума массива иллюстрирует общую схему циклических вычислений, применимую ко многим ситуациям. Вы определяете, что решением некоторой проблемы является элемент, принадлежащий n-мерной поверхности POST. В некоторых случаях POST может содержать ровно один элемент - решение, но обычно может быть более чем одно приемлемое решение проблемы. Циклы полезны, когда нет прямого способа достичь решения "одним выстрелом". Но у вас есть непрямая стратегия, вы можете, например, прицелиться и попасть в m-мерную поверхность INV, включающую POST (для m>n). Инвариантом является то, что поверхность попадания все время содержит POST. Итерация за итерацией приближаемся к POST, сохраняя истинность INV. Следующий рисунок иллюстрирует этот процесс:

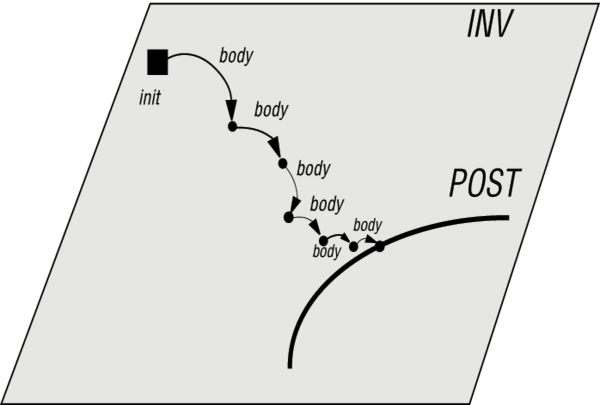
Рис. 11.8.  Вычисление цикла (из [М 1990])

Вычисление цикла имеет следующие ингредиенты:

[x]. Цель post, определяемую как свойство, выполняемое в любом допустимом заключительном состоянии. Пример: "Result является максимумом массива". На рисунке цель post представлена множеством состояний POST.

[x]. Инвариант цикла inv, являющийся обобщением цели, так что можно говорить, что цель - это частный случай инварианта. Пример: "Result является максимумом текущей нарезки массива". Инвариант цикла поиска цели, изображенный на рисунке: "Каждая точка лежит на поверхности, содержащей POST.

[x]. Точку инициализации init, о которой известно, что она должна быть в INV, другими словами должна обеспечить выполнение инварианта.

[x]. Преобразование body, начинающееся в INV, но не в POST, вырабатывающее точку более близкую к POST, но все еще остающуюся в INV. Тело цикла функции maxarray является примером подобного преобразования.

[x]. Верхняя граница числа применений body, необходимого для перевода точки из INV в POST. Как будет пояснено ниже, этот параметр необходим для определения варианта.

Последовательные приближения один из главных инструментов численного анализа. Но там эта идея понимается шире. Важная разница состоит в том, что в чистой математике допускаются бесконечные вычисления, последовательность может иметь предел, даже если он не достигается конечным числом приближений. Последовательность 1/n имеет предел 0, хотя среди членов последовательности нет числа 0. В компьютерных вычислениях мы хотим видеть результаты на нашем экране еще при нашей жизни, так что мы настаиваем, все аппроксимирующие последовательности достигают своей цели после конечного числа итераций.

Практический способ гарантии завершения циклического процесса состоит в связывании с итерационным процессом целочисленной величины - варианта цикла, обладающего следующими свойствами:

[x]. Вариант всегда не отрицателен.

[x]. Любое выполнение тела цикла уменьшает вариант.

Так как целочисленная неотрицательная величина не может уменьшаться бесконечно, то наличие варианта позволяет гарантировать завершение цикла. Вариант является верхней границей, максимальным числом применений body, приводящим точку в POST. В задаче нахождения максимума найти вариант просто: t.upper - i. Это выражение удовлетворяет обоим условиям:

[x]. Предусловие программы требует положительности t.capacity; другими словами, программа применима только к непустым массивам. Инвариант класса ARRAY задает: capacity = upper - lower + 1. Отсюда следует, что свойство i <= t.upper будет выполняться после инициализации i значением t.lower.

[x]. Любое выполнение тела цикла выполняет инструкцию i := i + 1, уменьшая вариант на единицу.

В этом примере цикл является простым итерированием на последовательности целых чисел в конечном интервале, известный в языках программирования, как "цикл For" или "цикл DO", завершение которого не трудно проверить. Для более изощренных циклов число требуемых итераций определить не так просто, выявление завершения становится сложной задачей, единственным универсальным способом является нахождение варианта.

Нам понадобится еще одно понятие, преобразующее только что набросанную схему в программный текст, описывающий цикл. Мы нуждаемся в простом способе определения того, что текущая итерация достигла цели (постусловия) post. Поскольку итерация конструируется так, чтобы обеспечить выполнение INV, а POST является частью INV, то обычно можно найти условие exit такое, что элемент из INV принадлежит POST тогда и только тогда, когда выполняется exit. Другими словами, постусловие post и инвариант inv связаны соотношением:

post = inv and exit

так что мы можем остановить цикл, - чьи промежуточные состояния по построению удовлетворяют inv, - как только выполнится exit. В этом состоянии, следовательно, будет выполнено и post.

Синтаксис цикла

Синтаксис цикла непосредственно следует из предшествующих соображений, определяющих ингредиенты цикла. Он будет включать элементы, отмеченные как необходимые.

[x]. Инвариант цикла inv - утверждение.

[x]. Условие выхода exit, чья конъюнкция с inv дает желаемую цель.

[x]. Вариант var - целочисленное выражение.

[x]. Множество инструкций инициализации, которые всегда приводят к состоянию, в котором inv выполняется, а var становится неотрицательным.

[x]. Множество инструкций body, которое (при условии, что оно начинается в состоянии, где var неотрицательно и выполняется inv), сохраняет инвариант и уменьшает var, в то же время следя за тем, чтобы оно не стало меньше нуля.

[x]. Синтаксис цикла честно комбинирует эти ингредиенты:

from
init
invariant
inv
variant
var
until
exit
loop
body
end

Предложения invariant и variant являются возможными. Предложение from по синтаксису требуется, но инструкция init может быть пустой.

Эффект выполнения цикла можно описать так: вначале выполняется init, затем 0 или более раз выполняется тело цикла, которое перестает выполняться, как только exit принимает значение false.

В языках Pasal, C и других такой цикл называется "циклом while", в отличие от цикла типа "repeat ... until", в котором тело цикла выполняется, по меньшей мере, один раз. Здесь же тест является условием выхода, а не условием продолжения, и синтаксис цикла явно содержит фазу инициализации. Потому эквивалент записи нашего цикла на языке Pascal выглядит следующим образом:

init;
while not exit do body

С вариантами и инвариантами цикл для maxarray выглядит так:

from
i := t.lower; Result := t @ lower
invariant
-- Result является максимумом нарезки массива t в интервале [t.lower,i].
variant
t.lower - i
until
i = t.upper
loop
i := i + 1
Result := Result.max (t @ i)
End

Заметьте, инвариант цикла выражен неформально, в виде комментария. Последующее обсуждение в этой лекции объяснит это ограничение языка утверждений.

Вот еще один пример, ранее показанный без вариантов и инвариантов. Целью следующей функции является вычисление наибольшего общего делителя - НОД (gcd - greatest common divisor) двух положительных целых a и b, следуя алгоритму Эвклида:

gcd (a, b: INTEGER): INTEGER is
-- НОД a и b
require
a > 0; b > 0
local
x, y: INTEGER
do
from
x := a; y := b
until
x = y
loop
if x > y then x := x - y else y := y - x end
end
Result := x
ensure
-- Result является НОД a и b
end

Как узнать, что функция gcd удовлетворяет своему постусловию и действительно вычисляет наибольший общий делитель a и b? Для проверки этого следует заметить, что следующее свойство истинно после инициализации цикла и сохраняется на каждой итерации:

x > 0; y > 0
-- Пара <x, y> имеет тот же НОД, что и пара <a, b>

Это и будет служить инвариантом цикла inv. Ясно, что inv выполняется после инициализации. Если выполняется inv и условие цикла x /= y, то после выполнения тела цикла:

if x > y then x := x - y else y := y - x end

инвариант inv остается истинным, замена большего из двух положительных неравных чисел их разностью не меняет их gcd и оставляет их положительными. Тогда по завершению цикла следует:

x = y and «Пара <x, y> имеет тот же НОД, что и пара <a, b>»

Отсюда, в свою очередь, следует, что x является наибольшим общим делителем. По определению НОД (x, x) = x.

Как узнать, что цикл всегда завершается? Необходим вариант. Если x больше чем y, то в теле цикла x заменяется разностью x-y. Если y больше x, то y заменяется разностью y-x. Нельзя в качестве варианта выбрать ни x, ни y, поскольку для каждого из них нет гарантии уменьшения. Но можно быть уверен, что максимальное из них обязательно будет уменьшено. Поэтому разумно выбрать в качестве варианта x.max(y). Заметьте, вариант всегда остается положительным. Теперь можно написать цикл со всеми предложениями:

from
x := a; y := b
invariant
x > 0; y > 0
-- Пара <x, y> имеет тот же НОД, что и пара <a, b>
variant
x.max (y)
until
x = y
loop
if x > y then x := x - y else y := y - x end
end

Как отмечалось, предложения invariant и variant являются возможными. Когда они присутствуют, то помогают прояснить цель цикла и проверить его корректность. Для любого нетривиального цикла характерны интересные варианты и инварианты; многие из примеров в последующих лекциях включают варианты и инварианты, обеспечивая глубокое понимание корректности лежащих в основе алгоритмов.

Оглавление книги