Книга: Основы объектно-ориентированного программирования
Обсуждение
Механизм утверждений, представленный в этой лекции, привносит несколько тонких проблем, подлежащих исследованию.
Нужен ли мониторинг в период выполнения?
Действительно, нужно ли проверять утверждения в период выполнения? После того, как мы были в состоянии, используя утверждения, дать теоретическое определение корректности класса: каждая процедура создания должна гарантировать инвариант, и тело каждой процедуры, запущенной в состоянии, удовлетворяющем инварианту и предусловию, сохраняет в заключительном состоянии инвариант и гарантирует выполнение постусловия. Теперь мы должны выполнить математическую проверку m+n соответствующих условий (для m процедур создания и n экспортируемых процедур), и тогда долой мониторинг в период выполнения.
Мы должны, но мы не можем. Доказательство правильности программ уже многие годы является активной областью исследований, и достигло определенных успехов. Все же сегодня невозможно проверить корректность реального ПО, написанного на современных языках программирования.
| Для этого необходим, в частности, и более мощный язык утверждений. Язык IFL, обсуждаемый ниже, может быть использован как часть стратегии многоярусного доказательства. |
Даже, если со временем методы и инструментальные средства доказательства станут доступными, можно ожидать, что отказаться от мониторинга не удастся. В системе всегда останется место трудно предсказуемым событиям - ошибкам аппаратуры, ошибкам в самом доказательстве. Поэтому следует применять хорошо известную в инженерии технику - множественные, независимые способы проверки.
Выразительная сила утверждений
Как можно было заметить, применяемый язык утверждений является языком обычных булевых выражений, обогащенный несколькими понятиями, такими как old. Как результат, он ограничен и не позволяет включить в наши классы некоторые свойства, достаточно просто выражаемые в математической нотации, используемой при описании АТД.
Утверждения класса стек дают хороший пример того, что выразимо, и что не выразимо в нашем языке. Мы найдем, что многие аксиомы и предусловия из спецификации АТД, приведенной в лекции 6, прямым образом отображаются в утверждения класса. Например, аксиома
A4. not empty (put (s, x))
задает постусловие not empty процедуры put. Но в некоторых случаях в классе нет непосредственного двойника. Ни одно из постусловий для remove, приводимое до сих пор, не отражает аксиому
A2. remove (put (s, x)) = s
Мы, конечно, можем ввести эту аксиому неформально, добавив в постусловие комментарий, описывающий это свойство:
remove is
-- Удалить элемент вершины
require
not_empty: not empty -- i.e. count > 0
do
count := count - 1
ensure
not_full: not full
one_fewer: count = old count - 1
LIFO_policy: -- item является последним элементом, помещенным в стек
-- и еще не удален, если таковое имело место.
End
Подобные неформальные утверждения, синтаксически выраженные комментариями, появлялись в инвариантах цикла для maxarray и gcd.
В таких случаях два из принципиальных использований утверждений, обсуждаемых ранее, остаются применимыми, по крайней мере, частично: помощь в создании корректного продукта и его документации (утверждения, заданные комментариями, будут появляться в краткой форме класса). Другие использования, в частности отладка и тестирование, предполагают вычисление выражений, и становятся теперь неприменимыми.
Было бы предпочтительнее выражать все утверждения формально. Лучший способ достичь этой цели - расширить язык выражений, так чтобы он позволял задавать любые свойства. Это требует возможности описания сложных математических объектов - множеств, последовательностей, функций, отношений. Необходим и мощный по выразительности язык, например, язык логики предикатов первого порядка, допускающий выражения с кванторами всеобщности и существования. Существуют формальные языки спецификаций, обладающие, по крайней мере, частью такой выразительной силы. Наиболее известными являются языки Z, VDM, Larch, OBJ-2; как Z, так и VDM имеют ОО-расширения, например, Object-Z. Библиографические замечания к лекции 6 дают необходимые ссылки.
Включение полного языка спецификаций в язык этой книги полностью изменило бы ее природу. Смысл языка в том, чтобы он был простым, легким в обучении, применимым во всех программистских конструкциях. Он должен допускать быструю компиляцию и эффективную реализацию с производительностью, соизмеримой с C или Fortran.
Вместо этого, в механизме утверждений мы пошли на инженерный компромисс: он включает достаточно формальных элементов, оказывающих существенный эффект на качество ПО, но останавливается в точке убывания - границе, за которой выгоды от большей формализации, начинают оборачиваться потерями простоты и эффективности.
| Определение границы во многом определяется личным выбором. Я был удивлен, для программистского сообщества в целом эта граница не изменилась со времен первого издания этой книги. Наша деятельность требует большего формализма, но профессиональное сообщество еще не осознало этого. |
Так что пока и на ближайшее будущее утверждения остаются булевыми выражениями с некоторыми расширениями. Это не такое уж и строгое ограничение, поскольку булевы выражения допускают вызов функций.
Включение функций в утверждения
Булевы выражения не ограничиваются использованием атрибутов и локальных сущностей. Мы уже использовали возможность вызова функций в утверждениях: предусловие для put класса стек было not full, где full - функция
full: BOOLEAN is
-- Is stack full? (Заполнен ли стек?)
do
Result := (count = capacity)
ensure
full_definition: Result = (count = capacity)
end
В этом наш маленький секрет, - мы вышли из рамок исчисления высказываний, в котором булевы выражения могут строиться только из переменных, констант и знаков логических операций. Благодаря введению функций, мы получили мощный механизм, позволяющий вычислять булевы значения любым, подходящим для нас способом. Не следует беспокоиться о присутствии постусловия самой функции full, это не создает никакого пагубного зацикливания. Детали вскоре.
Использование функций ведет к получению более абстрактных утверждений. Например, кто-то предпочтет заменить предусловие в операциях над массивом, ранее выраженное как
index_not_too_small: lower <= i
index_not_too_large: i <= upper
одним предложением в форме
index_in_bounds: correct_index (i)
с определением функции
correct_index (i: INTEGER): BOOLEAN is
-- Является ли i внутри границ массива?
do
Result := (i >= lower) and (i <= upper)
ensure
definition: Result = ((i >= lower) and (i <= upper))
end
Еще одно преимущество использования функций в выражениях в том, что они дают способ обойти ограничения выразительной силы, возникающие из-за отсутствия механизмов логики предикатов первого порядка. Неформальный инвариант нашего цикла для maxarray
-- Result является максимумом нарезки массива t в интервале [t.lower,i]
формально может быть выражен так
Result = (t.slice (lower, i)).max
в предположении, что slice вырабатывает нарезку - массив с индексами от lower до i, - а функция max дает максимальный элемент этого массива.
| Этот подход был исследован в [M 1995a] как способ расширения выразительной силы механизма утверждений, возможно ведущий к разработке полностью формального метода, - другими словами, к математическому доказательству корректности ПО. В этом исследовании есть две центральные идеи. Первая - использование библиотек в процессе доказательства, так что можно его проводить для реальных, широкомасштабных систем, строя многоярусную структуру, использующую условные доказательства. Вторая идея - определение ограниченного языка чисто аппликативной природы - IFL (Intermediate Functional Language), в котором выражаются функции, используемые в выражениях. Язык IFL является подмножеством нотации этой книги, включающий некоторые императивные конструкции, такие как любые присваивания. |
Ясно, чем мы рискуем: появление функций в выражениях означает введение потенциально императивных элементов (программ) в чисто аппликативный, до сего времени, мир утверждений. Без функций мы имели ясное и четкое разделение ролей, обсуждаемое ранее: инструкции предписывают, утверждения описывают. Теперь мы открыли ворота аппликативного города императивным полчищам.
Все же трудно сопротивляться мощи использования функций, поскольку все альтернативы имеют свои недостатки.
[x]. Включение полного языка спецификаций, как отмечалось, приводит к потере эффективности и простоты изучения.
[x]. Вероятно, хуже то, что неясно, достаточны ли общепринятые языки утверждений. Возьмем, например, такого естественного кандидата, в которого многие верят, - язык логики предикатов первого порядка. Этот формализм не позволяет нам выразить некоторые свойства, представляющие непосредственный интерес для разработчиков и часто используемые в утверждениях, такие как, например, "граф не имеет циклов" (типичный инвариант цикла). Математически это может быть выражено как r+
Все это создает больше трудностей для программиста, которому проще написать булеву функцию cyclic, исследующую граф и возвращающую true, если и только если в графе есть цикл. Такие примеры являются серьезными аргументами в пользу базисного языка утверждений с использованием функций для повышения его выразительной силы.
Но остается необходимость разделять императивные и аппликативные элементы. Любая программно реализованная функция, используемая в утверждениях для специфицирования свойств, должна быть "безупречной", без обвинений ее в императивности, - она не должна быть причиной никаких изменений абстрактного состояния.
Это неформальное требование достаточно ясно на практике; формализм подъязыка IFL исключает все императивные элементы, которые либо изменяют глобальное состояние системы, либо не имеют тривиальных аппликативных эквивалентов, в частности исключаются:
[x]. присваивания атрибутам;
[x]. присваивания в циклах;
[x]. вызовы программ, не входящих в IFL.
Если особо тщательно дирижировать функциями, достаточно простыми с очевидной корректностью, то использование в утверждениях программно реализованных функций дает мощный метод абстракции.
Некоторые технические вопросы могут потребовать внимания. Функция f, используемая в утверждении программы r, может сама иметь утверждения, что демонстрируют примеры функций full и correct_index. Возникает потенциальная проблема при мониторинге утверждений в период выполнения: если при вызове r мы вычисляем утверждение, вызывающее f, то не придется ли нам вычислять утверждение для f? Нетрудно сконструировать пример зацикливания, если пойти по этому пути. Но даже и без этого риска было бы неправильно вычислять утверждение для f. Это бы означало, что мы рассматриваем "на равных" программы, являющиеся предметом наших вычислений, такие как r, и их функции утверждения, такие как f. В противовес этому сформулируем правило, согласно которому утверждения должны иметь более высокий приоритет, чем программы, которые они защищают, их корректность должна быть кристально ясной. Правило простое:
Правило вычисления утверждения
В процессе вычисления утверждений, входящие в них вызовы программ должны выполняться без вычисления ассоциированных утверждений.
Если вызов f встречается как часть проверки утверждения программы r, то слишком поздно спрашивать, удовлетворяет ли f своим утверждениям. Подходящим является время, когда решается вопрос использования f в утверждении, применимом к r.
Рассматривайте f как охранника ядерного предприятия, в обязанности которого входит проверка посетителей. Охранников тоже нужно проверять, но не тогда, когда они сопровождают посетителей.
Инварианты класса и семантика ссылок
ОО-модель, разрабатываемая до сих пор, включала два частично не связанных аспекта, оба из которых полезны:
[x]. Понятие инварианта класса, введенное в этой лекции.
[x]. Гибкая модель периода выполнения, детально рассмотренная в начальных лекциях, существенно использующая ссылки.
К несчастью, эти индивидуально желательные свойства могут стать причиной трудностей при их совместном использовании.
Проблема вновь в динамически создаваемых псевдонимах, предохраняющих нас от проверки корректности класса на том основании, что класс делает это сам. Мы уже видели, что корректность класса означает проверку m+n свойств, выражающих следующее (если мы концентрируем внимание на инвариантах INV, игнорируя предусловия и постусловия, не играющие здесь роли):
1 Каждая из m процедур создания порождает объект, удовлетворяющий INV.
2 Каждая из n экспортируемых программ сохраняет INV.
Кажется, совместно эти два условия гарантируют, что INV действительно инвариант. Доказательство почти тривиально: так как INV удовлетворяется в момент создания и сохраняется при каждом вызове, то по индукции INV истинно во все стабильные времена.
Это неформальное доказательство, однако, не верно в присутствии семантики ссылок и динамических псевдонимов. Проблема в том, что атрибуты объекта могут модифицироваться операциями другого объекта. Даже если a.r сохраняет INV для объекта ОА, присоединенного к а, то некоторая операция b.s (для b, присоединенного к другому объекту,) может разрушить INV для ОА. Так что условия (1) и (2) могут выполняться, но INV может не быть инвариантом.
Вот простой пример. Предположим, что А и В классы, каждый из которых содержит атрибут другого класса:
class A ... feature forward: B ... end
class B ... feature backward: A ... end
Потребуем, чтобы ссылки были связаны содержательным условием. Если ссылка forward определена и задает экземпляр класса В, то ссылка backward этого экземпляра, в свою очередь, должна указывать на соответствующий экземпляр класса А. Это может быть выражено как инвариант класса А:
round_trip: (forward /= Void) implies (forward.backward = Current)
Вот пример ситуации, включающей экземпляры обоих классов и удовлетворяющей инварианту:
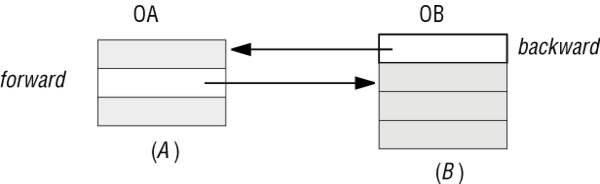
Рис. 11.9. Согласованность ссылок forward и backward
Инвариант round_trip встречается в классах довольно часто. Например, в роли класса А может выступать класс PERSON, характеризующий персону. Ссылка forward может указывать в этом случае на владение персоны - объект класса HOUSE. Ссылка backward в этом классе указывает на владельца дома. Еще одним примером может быть реализация динамической структуры - дерева, узел которого содержит ссылки на старшего сына и на родителя. Для этого класса можно ввести инвариант в стиле round_trip:
Предположим, что инвариант класса В, если он есть, ничего не говорит об атрибуте backward. Следующая версия класса А по-прежнему имеет инвариант:
class A feature
forward: B
attach (b1: B) is
-- Ссылка b1 на текущий объект.
do
forward := b1
-- Обновить ссылку backward объекта b1 для согласованности:
if b1 /= Void then
b1.attach (Current)
end
end
invariant
round_trip: (forward /= Void) implies (forward.backward = Current)
end
Вызов b1.attach восстанавливает инвариант после обновления forward. Класс В должен обеспечить свою собственную процедуру attach:
class B feature
backward: B
attach (a1: A) is
-- Ссылка a1 на текущий объект.
do
backward := a1
end
end
Класс А сделал все для своей корректности: процедура создания по умолчанию гарантирует выполнение инварианта, так как устанавливает forward равным void, а его единственная процедура гарантирует истинность инварианта. Но рассмотрим выполнение у клиента следующей программы:
a1: A; b1: B
...
create a1; create b1
a1.attach (b1)
b1.attach (Void)
Вот ситуация после выполнения последней инструкции:
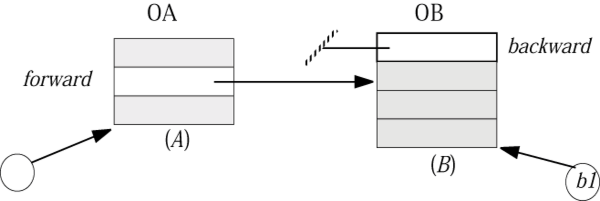
Рис. 11.10. Нарушение инварианта
Инвариант для ОА нарушен. Этот объект теперь указывает на ОВ, но ОВ не указывает на ОА, - backward равно void. Вызов b1.attach мог связать ОВ с любым другим объектом класса А и это тоже было бы некорректно.
Что случилось? Динамические псевдонимы вновь себя проявили. Приведенное доказательство корректности класса А правильно, и единственная процедура этого класса attach спроектирована в полном соответствии с замыслом. Но этого недостаточно для сохранения согласованности ОА, так как свойства ОА могут включать экземпляры других классов, а доказательство ничего не говорит об эффекте, производимом свойствами других классов на инвариант из А.
Эта проблема достаточно важна, и заслуживает собственного имени: Непрямой Эффект Инварианта (Indirect Invariant Effect). Он может возникать сразу же при допущении динамических псевдонимов, благодаря которому операции могут модифицировать объекты даже без включения любой связанной сущности. Но мы уже видели, как много пользы приносят динамические псевдонимы; и схема forward - backward далеко не академический пример, это, как отмечалось, полезный образец для практических приложений и библиотек.
Что можно сделать? Промежуточный ответ включает соглашения для мониторинга утверждений в период выполнения. Вы, возможно, удивлялись, почему эффект включения мониторинга утверждений на уровне assertion (invariant) был описан так:
"Проверка выполнимости инвариантов класса на входе и выходе программы для квалифицированных вызовов".
Почему и на входе и на выходе? Без Непрямого Эффекта Инварианта достаточно было бы проверки на выходе, при условии проверки процедур создания. Но теперь мы должны быть более аккуратными, поскольку между завершением одного вызова и началом вызова другой операции над тем же объектом, могут быть вызовы, задевающие объект, даже если в роли цели выступал совсем другой объект.
Более удовлетворительное решение могло быть получено включением статистического правила, имеющего обязательную силу, гарантирующего, что всякий раз, когда инвариант класса А включает ссылки на экземпляры класса В, инвариант в классе В должен быть зеркальным отображением инварианта из А. В нашем примере можно избежать всех трудностей, включив в класс В инвариант:
trip_round: (backward /= Void) implies (backward.forward = Current)
Быть может, возможно, обобщить это правило в универсальное правило отображения. Вне зависимости от того, существует ли такое обещающее правило или нет, решение проблемы Непрямого Эффекта Инварианта и избавление необходимости двойной проверки при мониторинге инвариантов требует дальнейших исследований.
Что дальше
Еще не все сделано с Проектированием по контракту. Предстоит изучить два важных следствия рассмотренных принципов:
[x]. Как они приводят к механизму дисциплинированной обработки исключений; это тема следующей лекции.
[x]. Как они комбинируются с наследованием, позволяя нам указать, что любые семантические ограничения, применимые к классу, применимы также и к его потомкам; и что семантические ограничения, применимые к компоненту, применимы и при возможных его переопределениях. Эта тема будет изучаться при рассмотрении наследования.
Обобщая, утверждения и Проектирование по контракту будут сопровождать нас во всей оставшейся части этой книги, позволяя проверить, знаем ли мы, что делают создаваемые нами элементы.




