Книга: Учебное пособие по курсу «Нейроинформатика»
Двуслойность персептрона
Двуслойность персептрона
Как уже упоминалось ранее в данной главе возможно использование многослойных персептронов. Однако теоремы о сходимости и зацикливании персептрона, приведенные выше верны только при обучении однослойного персептрона, или многослойного персептрона при условии, что обучаются только веса персептрона, стоящего в последнем слое сети. В случае произвольного многослойного персептрона они не работают. Следующий пример демонстрирует основную проблему, возникающую при обучении многослойных персептронов по правилу Хебба.
Пусть веса всех слоев персептрона в ходе обучения сформировались так, что все примеры обучающего множества, кроме первого, решаются правильно. При этом правильным ответом первого примера является 1. Все входные сигналы персептрона последнего слоя равны нулю. В этом случае первое правило Хебба не дает результата, поскольку все нейроны предпоследнего слоя не активны. Существует множество методов, как решать эту проблему. Однако все эти методы не являются регулярными и не гарантируют сходимость многослойного персептрона к решению даже при условии, что такое решение существует.
В действительности проблема настройки (обучения) многослойного персептрона решается следующей теоремой.
Теорема о двуслойности персептрона. Любой многослойный персептрон может быть представлен в виде двуслойного персептрона с необучаемыми весами первого слоя.
Для доказательства этой теоремы потребуется одна теорема из математической логики.
Теорема о дизъюнктивной нормальной форме. Любая булева функция булевых аргументов может быть представлена в виде дизъюнкции конъюнкций элементарных высказываний и отрицаний элементарных высказываний:
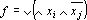
Напомним некоторые свойства дизъюнктивной нормальной формы.
Свойство 1. В каждый конъюнктивный член (слагаемое) входят все элементарные высказывания либо в виде самого высказывания, либо в виде его отрицания.
Свойство 2. При любых значениях элементарных высказываний в дизъюнктивной нормальной форме может быть истинным не более одного конъюнктивного члена (слагаемого).
Доказательство теоремы о двуслойности персептрона. Из теоремы о дизъюнктивной нормальной форме следует, что любой многослойный персептрон может быть представлен в следующем виде:
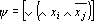
В силу второго свойства дизъюнктивной нормальной формы (5) можно переписать в виде
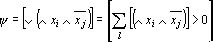
Переведем в арифметическую форму все слагаемые в (6). Конъюнкция заменяется умножением, а отрицание на разность:
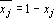
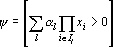
где Il — множество индексов сомножителей в l-м слагаемом, ?l — число, указывающее сколько раз такое слагаемое встретилось в (6) после замены и раскрытия скобок (число подобных слагаемых).
Заменим i-е слагаемое в (7) персептроном следующего вида:
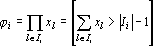
Подставив (8) в (7) получим (1), то есть произвольный многослойный персептрон представлен в виде (1) с целочисленными коэффициентами. В качестве персептронов первого слоя используются персептроны вида (8) с необучаемыми весами. Теорема доказана.
Подводя итоги данной главы следует отметить следующие основные свойства персептронов:
1. Любой персептрон может содержать один или два слоя. В случае двухслойного персептрона веса первого слоя не обучаются.
2. Веса любого персептрона можно заменить на целочисленные.
3. При обучении по правилу Хебба после конечного числа итераций возможны два исхода: персептрон обучится или вектор весов персептрона будет повторяться (персептрон зациклится).
Знание этих свойств позволяет избежать «усовершенствований» типа модификации скорости обучения и других, столь же «эффективных» модернизаций.




