Книга: Учебное пособие по курсу «Нейроинформатика»
Целочисленность весов персептронов
Целочисленность весов персептронов
В данном разделе будет доказана следующая теорема.
Теорема. Любой персептрон (1) можно заменить другим персептроном того же вида с целыми весами связей.
Доказательство. Обозначим множество примеров одного класса (правильный ответ равен 0) через X0, а другого (правильный ответ равен 1) через X1. Вычислим максимальное и минимальное значения суммы в правой части (1):
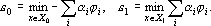
Определим допуск ? как минимум из s0 и s1. Положим ?=s/(m+1) , где m — число слагаемых в (1). Поскольку персептрон (1) решает поставленную задачу классификации и множество примеров в обучающей выборке конечно, то ?>0. Из теории чисел известна теорема о том, что любое действительное число можно сколь угодно точно приблизить рациональными числами. Заменим веса ?i на рациональные числа так, чтобы выполнялись следующие неравенства |?i-?i'|<?.
Из этих неравенств следует, что при использовании весов ?i' персептрон будет работать с теми же результатами что и первоначальный персептрон. Действительно, если правильным ответом примера является 0, имеем
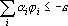
Подставив новые веса, получим:
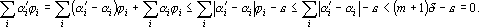
Откуда следует необходимое неравенство

Аналогично, в случае правильного ответа равного 1, имеем
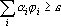
, откуда, подставив новые веса и порог получим:
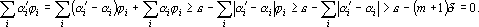
Откуда следует выполнение неравенства
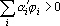
Неравенства (2) и (3) доказывают возможность замены всех весов и порога любого персептрона рациональными числами. Очевидно так же, что при умножении всех весов и порога на одно и тоже ненулевое число персептрон не изменится. Поскольку любое рациональное число можно представить в виде отношения целого числа к натуральному числу, получим
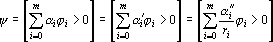
где ?i? — целые числа. Обозначим через r произведение всех знаменателей
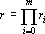
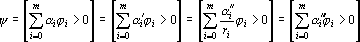
что и завершает доказательство теоремы.
Поскольку из доказанной теоремы следует, что веса персептрона являются целыми числами, то вопрос о выборе шага при применении правила Хебба решается просто: веса и порог следует увеличивать (уменьшать) на 1.




