Книга: Написание скриптов для Blender 2.49

Мыльные пузыри — шейдер, зависимый от точки зрения

Мыльные пузыри — шейдер, зависимый от точки зрения

У некоторых материалов вид меняется в зависимости от угла, под которым мы на них смотрим. Перья птиц, некоторые причудливые автомобильные краски, нефтяные разливы на воде, и мыльные пузыри - вот несколько примеров. Этот феномен изменения цветов известен как радужность (iridescence). Если мы хотим осуществить нечто подобное, нам нужен доступ к вектору вида и нормали поверхности. В нашем шейдере мыльного пузыря мы увидим один из способов сделать это.

Сначала немного математики: Почему это мыльные пузыри показывают все эти различные цвета? Мыльные пузыри - это в основном искривлённые водяные плёнки (с небольшим количеством мыла), и свет отражается от поверхности раздела между воздухом и водой. Следовательно, падающий луч частично отражается, когда он попадает на внешнюю поверхность пузыря, и отражается снова, когда он достигает внутренней поверхности. Следовательно, отраженный свет, который попадает в глаз — является суммой света, прошедшего различные расстояния; часть его прошла дополнительное расстояние в две толщины мыльного пузыря.

Теперь учтём, что свет ведет себя подобно волне, а волны, которые интерферируют, могут или ослаблять или усиливать друг друга в зависимости от их фазы, и поэтому, два световых луча, прошедшие расстояния, разница которых не кратна в точности их длине волны, гасят друг друга. В результате, белый свет (континуум, совокупность цветов), отраженный мыльным пузырём с толщиной, равной половине длины волны некоторого специфического цвета, покажет только этот единственный цвет, поскольку все остальные цвета подавлены, так как они "не соответствуют" должным образом толщине между внутренней и внешней поверхностью. (Существует гораздо больше информации о мыльных пузырях. Для большей и более   точной   информации   вот   ссылка: http://ru.wikipedia.org/wiki/Мыльные_пузыри.)

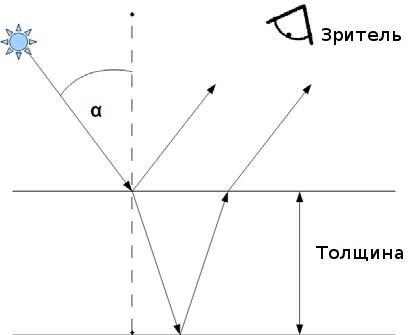
Теперь мы знаем, что расстояние пройденное между двумя отражающими поверхностями, определяет цвет, который мы воспринимаем, мы можем также понять, почему цвет будет варьироваться в мыльном пузыре. Первым фактором является кривизна пузыря. Пройденное расстояние будет зависеть от угла между падающим светом и поверхностью: чем меньше угол, тем более длинное расстояние свет должен пройти между поверхностями. Угол падения изменяется, так как поверхность кривая, и таким образом, изменяется расстояние, и, следовательно, цвет. Второй причиной изменения цвета является неравномерность поверхности: незначительные изменения из-за тяжести или вихри, вызванные воздушными течениями или перепадами температур, также вызывают различия в цвете.

Вся эта информация переводится в удивительно короткую часть кода (полный код доступен как  irridescence.py в файле irridescence.blend вместе с примером нодовой сети).

Наряду с координатами, у нас есть ещё два входных сокета — один для толщины водяной плёнки и один для вариаций. Вариации будут добавляться к толщине и этот сокет может быть присоединён к текстурному ноду, чтобы генерировать вихри и тому подобное. У нас есть единственный выходной сокет для рассчитанного расстояния: class Iridescence(Node.Scripted):

   def __init__(self, sockets):
      sockets.input = [
         Node.Socket('Coords', val= 3*[1.0]),
         Node.Socket('Thickness', val=275.0,
                      min=100.0, max=1000.0),
         Node.Socket('Variation', val=0.5, min=0.0,
                      max=1.0)]
      sockets.output = [Node.Socket('Distance',
                        val=0.5, min=0.0, max=1.0)]

Вычисления отраженного цвета начинается с получением списка всех ламп на сцене, так как мы хотим вычислить угол падающих световых лучей. Сейчас, мы принимаем во внимание вклад только первой лампы, которую мы нашли. Тем не менее, более полная реализация должна рассматривать все лампы, и может быть, даже их цвет. Для наших вычислений мы должны убедиться, что нормаль поверхности N и вектор падения света L находятся в одном и том же пространстве. Так как предоставляемая нормаль поверхности будет в пространстве камеры, мы должны трансформировать этот вектор матрицей преобразования камеры, как мы это делали для нашего наклоно-зависимого шейдера (выделено в следующем куске кода):

   def __call__(self):
      P = vec(self.input.Coords)
      scn=Scene.GetCurrent()
      lamps = [ob for ob in scn.objects if
               ob.type == 'Lamp']
      lamp = lamps[0]
      cam=scn.objects.camera
      rot=cam.getMatrix('worldspace').rotationPart(
                                       ).resize4x4();
      N = vec(self.shi.surfaceNormal).normalize(
                                       ).resize4D() * rot
      N = N.negate().resize3D()
      L = vec(lamp.getLocation('worldspace'))
      I = (P – L).normalize()

Затем, мы вычисляем угол между нормалью поверхности и вектором падения (VecT - псевдоним для функции Mathutils.angleBetweenVecs()), и используем этот угол падения, чтобы вычислить угол между нормалью поверхности внутри водяной плёнки, так как он определяет расстояние прохождения света. Мы используем закон Снелла для его вычисления, а для   показателя преломления водной плёнки возьмём 1.31. Расчет расстояния после этого - вопрос простой тригонометрии (выделено ниже):

      angle = VecT(I,N)
      angle_in = pi*angle/180
      sin_in = sin(angle_in)
      sin_out = sin_in/1.31
      angle_out = asin(sin_out)
      thickness = self.input.Thickness +
                  self.input.Variation
      distance = 2.0 * (thickness / cos (angle_out))

Рассчитанное расстояние равняется длине волны цвета, который мы воспримем. Тем не менее, Блендер работает не с длинами волн, а с цветами RGB, так что нам всё еще нужно преобразовать эту длину волны в кортеж (R, G, B), который представляет тот же цвет. Это можно было бы сделать посредством применения некоей спектральной формулы (смотрите, например, здесь: http://www.philiplaven.com/p19.html), но, может   быть,   будет   даже   более универсальным вариантом масштабировать это рассчитанное расстояние, и использовать его как вход для цветовой полосы (color band). Таким образом мы можем воспроизвести   не-физически   точную радужность (если захотим):

      self.output.Distance = distance

Чтобы использовать этот Pynode, нужно иметь в виду некоторые моменты. Сначала, убедитесь, что рассчитанный цвет влияет только на цвет specular материала мыльного пузыря, в противном случае всё покажется вымытым.

Кроме того, важно добавлять некоторое изменение к толщине слоя, так как никакой реальный мыльный пузырь не имеет точной однородной толщины. Выбор текстуры шума может привести к очень различному виду. В следующем примере нодовой сети мы добавили на вход немного шумовой текстуры wood, чтобы получать вихревые полосы, часто обнаруживаемые на мыльных плёнках.

Наконец, сделайте материал мыльной плёнки очень прозрачным, но с высокой отражательной способностью (specular). Экспериментируйте с величинами, чтобы добиваться точного эффекта, и примите во внимание настройку освещения. Пример, показанный на иллюстрации – пробный, чтобы получить некий результат в черно-белом представлении, и, следовательно, не реалистичен, но сеть в файле примера iridescence.blend настроена производить красочный приятный результат при рендере.

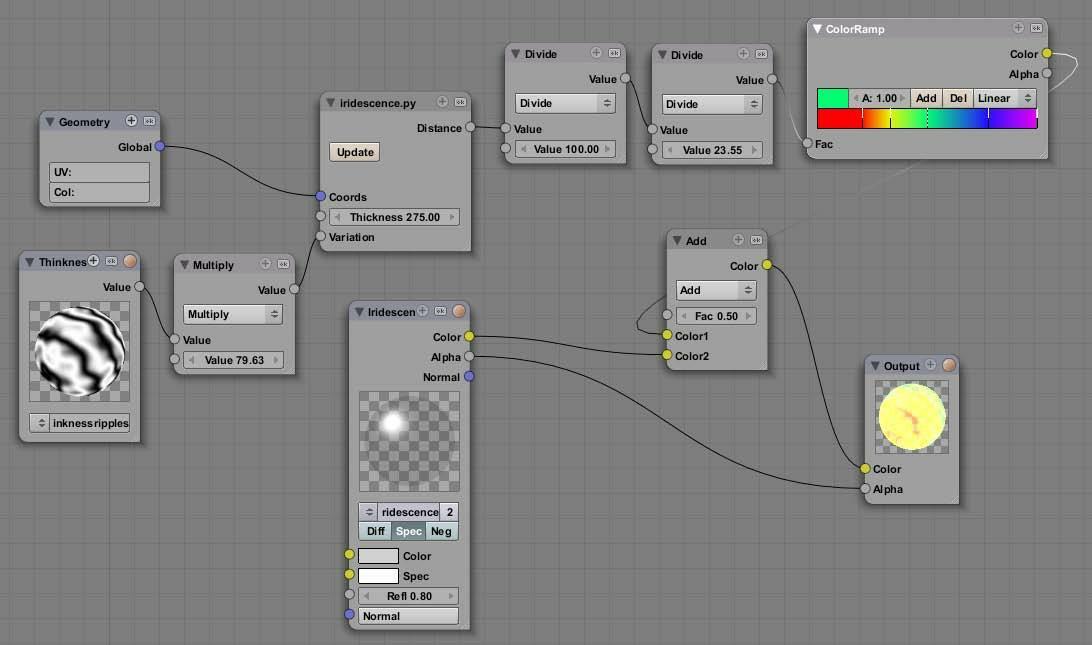
Использование color ramp и текстуры шума показано на предыдущем скриншоте, куда мы добавили несколько нодов деления, чтобы масштабировать наше расстояние в дипазон в пределах [0,1], который можно использовать как вход для color ramp:

Оглавление книги