Книга: Написание скриптов для Blender 2.49

Вы тоже находите меня притягательным?

Когда Луна и Земля вращаются вокруг друг друга, каждая из них чувствует гравитационное притяжение другой. На земле это приводит к приливам и отливам, но твердые тела Земли и Луны также исказятся, хотя этот эффект небольшой. Теперь известно намного больше о приливах и отливах, чем только притяжение (http://ru.wikipedia.org/wiki/Прилив_и_отлив), но мы можем показать гравитационные искажения в гипертрофированном виде с применением ограничений.

Один из способов сделать это - использовать ограничение TrackTo, чтобы ориентировать ось нашего ограничиваемого объекта к притягивающему объекту и добавить второе ограничение, которое масштабирует ограничиваемый объект вдоль этой оси. Величина масштаба будет обратно зависима от расстояния между ограничиваемым объектом и целевым объектом. Эффект проиллюстрирован на следующем скриншоте, где эффект ограничения TrackTo объединен со скриптовым ограничением moon_constraint.py.

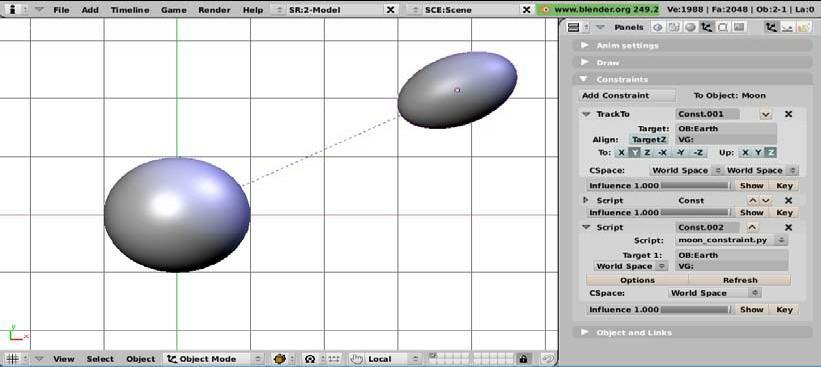
Мы должны написать это зависимое от расстояния масштабирование самостоятельно. Если мы возьмём шаблон ограничения, предоставляемый Блендером, мы можем оставить функции doTarget() и getSettings() как есть, но мы должны написать подходящую doConstraint() (полный код доступен как moon_constraint.py):

def doConstraint(obmatrix, targetmatrices, idprop):
    obloc = obmatrix.translationPart() # Положение
    obrot = obmatrix.toEuler()         # Вращение
    obsca = obmatrix.scalePart()       # Масштаб
    tloc = targetmatrices[0].translationPart()
    d = abs((obloc-tloc).length)
    d = max(0.01,d)
    f = 1.0+1.0/d
    obsca[1]*=f
    mtxloc = Mathutils.TranslationMatrix(obloc)
    mtxrot = obrot.toMatrix().resize4x4()
    mtxsca = Mathutils.Matrix([obsca[0],0,0,0],
             [0,obsca[1],0,0],[0,0,obsca[2],0], [0,0,0,1])
    outputmatrix = mtxsca * mtxrot * mtxloc
    return outputmatrix

Мы пропустили все строки, имеющие отношение к свойствам, так как мы не используем никаких настраиваемых пользователем свойств для этого ограничения. Выделенные строки показывают, что мы должны делать для вычисления зависимого от расстояния масштабирования.

В первой строке получаем позицию нашей цели. Затем   мы   вычисляем   расстояние   между ограничиваемым объектом и целью и определяем предел его минимума (чуть-чуть больше нуля), чтобы предотвратить деление на нуль в следующей выделенной строке. Используемая здесь формула отнюдь не является аппроксимацией какого-либо гравитационного влияния, но ведет себя достаточно хорошо   для   наших   целей;   коэффициент масштабирования будет близок к 1.0, если d очень большое, и гладко возрастает при уменьшении расстояния d. Последняя выделенная строка показывает, что мы изменяем масштаб только по оси y, то есть по оси, которую мы ориентируем на целевой объект с помощью ограничения TrackTo.

Если оба объекта имеют сравнимую массу, гравитационное искажение должно быть сравнимого размера на обоих объектах. У нас может появиться искушение добавить  ограничения TrackTo и moon_constraint.py к обоим объектам, чтобы видеть эффект воздействия их друг на друга, но, к несчастью, это не будет работать, поскольку это создаст циклическую зависимость, и Блендер запротестует.

Оглавление книги