Книга: Сервисный компас

Золотое сечение

Золотое сечение

~~~

Один порождает два,

Два порождает три,

Три порождает все многообразие вещей…

(Лао Цзы)

~~~

Именно в такой формулировке приписывают изречение великому восточному мыслителю. Мы почему-то привыкли к таким выражениям, как к неким сакральным изречениям древних мудрецов, не несущих практического смысла. А зря! Ведь хорошо понятые сакральные вещи, на практике, могут оказаться намного полезнее многих трудов некоторых ученых! Думаю, что выражение «Один порождает два, Два порождает три, три порождает все многообразие вещей…» стоит отдельного осмысления. Для начала стоит хорошенько осмыслить ключевую фразу «Один порождает два», что мы успешно уже начали делать.

Но что за бред! И зачем задумываться обо всем этом, просыпаясь утром, слушая новости, вталкиваясь в метро, споря с друзьями о футболе и политике и успешно реализуя очередной бизнес-проект?

Хочу поделиться одним интересным наблюдением из своих школьных лет, когда я довольно активно интересовался законами физики, не принимая многие вещи на веру, пытаясь пропускать все через свой личный опыт. Как-то раз, мы старшими классами впервые проходили медкомиссию в военкомате. Все проходило довольно скучно, за исключением одного кабинета, в котором проверяли психологический уровень и IQ будущих призывников. Волнуясь, как и все, чтобы не попасть впросак, я стоял под кабинетом и спрашивал выходящих о задаваемых вопросах. Ключевыми оказались: произнесение скороговорки, знание таблицы умножения, интерпретация пословицы типа «Семеро одного не ждут» и, наконец, формулировка одного из простых физических законов, среди которых самым популярным был закон Архимеда. Ну и что ты ответил? – интересовался я у очередного подростка и слышал примерно одинаковый ответ: «Ну как же!? Тело, погруженное в жидкость, вытесняет…». На этом, как правило, ответ обрывался, что, впрочем, не мешало получать им «зачет».

Вспоминая не без улыбки эту историю, уже в зрелом возрасте, я начал задавать этот же вопрос взрослым людям и обнаружил, что правильный ответ выдает только примерно каждый пятый. У остальных четверых наблюдалась примерно одинаковая картина, начинавшаяся с фразы «Ну это же просто!». Затем следовало смущение, сменявшееся уверенностью, ведь нельзя же уронить лицо в незнании школьной программы. Затем следовали фразы типа «Тело, погруженное в жидкость, вытесняет…» либо, в лучшем случае «На тело, погруженное в жидкость действует сила…». Затем наступала немая сцена.

Вот так. Слушаем, но не слышим! Смотрим, но не видим! Уверены, что понимаем, но не можем объяснить! Если и вы попались на удочку, я сознательно не буду приводить здесь правильной и изящной формулировки, данной великим Архимедом.

Примерно такая же участь была уготована историей понятию «Золотое сечение». Все о нем слышали, все знают о некой Золотой середине, которую надо искать и на которой, как правило, находится оптимальное решение. Но почему-то из пары слов «Золотая середина», многие слышат только слово «середина», в принципе не задумываясь, а почему собственно «Золотая». Многие помнят, что золотое сечение использовал в своих картинах Леонардо Давинчи… Мне лично, всю жизнь не давал покоя вопрос, а кто, что и у кого отсекает? Поскольку вопрос важный и ключевой, предлагаю остановиться на его понимании подробнее. Именно здесь вступают в силу два самых красивых и базовых числа, творящих гармонию нашего мира – числа «Пи» и «Фи», числа 3.142… и 1.618… Оба эти числа связаны с именами математиков «первооткрывателей» – греком Пифагором и итальянцем Фибоначчи, хотя конечно же эти числа были известны человечеству намного раньше.

Сначала о числе «Пи». Напомню, и еще раз поставлю под сомнение школьную программу по геометрии, трактующую прямую линию и отрезок как первичные понятия по отношению к окружности. Программа также концентрируется на готовых, построенных из отрезков многоугольниках, не отвечая на вопрос, откуда берутся точки, формирующие вершины этих многоугольников (рис). Школьная геометрия говорит, что есть две первичные точки, между которыми формируется реальная прямая линия. Или одну из этих реальных точек можно объявить центром окружности, а при помощи второй очертить саму окружность. Все очень логично, но так ли это в реальной природе?

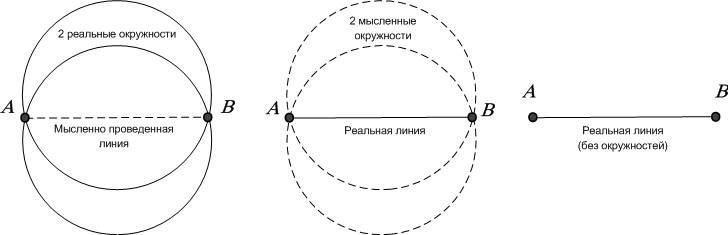
Рис. Две окружности, формирующие отрезок

или отрезок, не знающий о своем происхождении?

Ведь если посмотреть на окружающий мир, в нем нет ни одной прямой линии и тем более квадратов и кубов. Все вокруг состоит из соединения дуг окружностей или частей сфер разного радиуса. Все, что выполнено в виде прямых линий, идеальных поверхностей и точек излома, либо является абстракцией восприятия нашего сознания, либо создано искусственно руками человека.

Так что же мы тогда делаем на самом деле, решая задачу о квадратуре круга, сравнивая между собой квадрат и окружность? мы берем естественный квадрат и вписываем в него окружность или берем окружность и мысленно размещаем квадраты внутри и вовне?

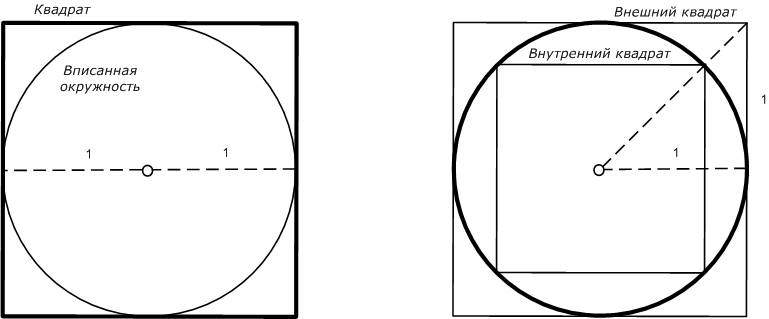
Рис. Окружность, вписанная в квадрат

или квадраты, размещенные вне и внутри окружности?

Похоже, что первична и естественна окружность единичного радиуса и двойного диаметра. Вокруг нее мы можем построить квадрат, в пропорциях которого и проявляется число Пи = 3,1415926…, или можем вписать квадрат, в пропорциях которого проявляется «Квадратный корень» и теорема Пифагора. Так что мы обнаруживаем не диаметр, творящий окружность, а окружность, проявляющая в себе диаметр, прямую линию и правильные многоугольники.

Все эти рассуждения в полной мере относятся не только к окружностям и квадратам, но и пространственным сферам и кубам. Именно пересечение окружностей в двумерном пространстве и сфер в трехмерном пространстве определяет все многообразие форм в природе, а уже соединяя мысленно или физически точки этих пересечений мы получаем фигуры, состоящие из вершин, углов, ребер и граней. В реальной природе нет прямых линий, а есть игра окружностей и гармония сфер.

Единственное, к чему можно условно применить понятие прямых – это противоположные направления: верх и низ, право и лево, север и юг… Но для этого за них надо зацепиться, как за точку опоры, которую так искал Архимед, объявить эту точку началом отсчета и построить ортогональные Декартовы оси координат. Но об этом позже, а пока, обратимся к Золотому сечению и второму волшебному числу «Фи» = 1.618..

Рискну немного переформулировать изречение великого древнего мыслителя, оперируя не натуральными, а иррациональными числами:

«Фи» порождает «Два». Два порождает все многообразие вещей.

Для проверки, мы вернемся к первой вибрации, разделяющей белое и черное. Здесь важно понимать, что белое и черное не отделяются друг от друга полностью, иначе они бы стали полностью независимы друг от друга. Чтобы быть во взаимной зависимости, они всегда находятся в смешанном состоянии, в какой-то строго определенной пропорции.

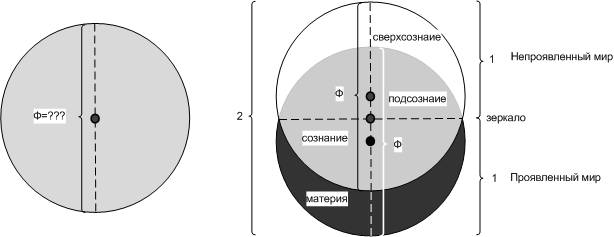
Рис. «Фи» порождает два

Иными словами, находясь в материальной нижней единичной половинке, я могу проявить только строго определенную часть нематериальной верхней половинки. Оставшаяся же верхняя часть всегда будет непроявленной внизу. И наоборот. Так что же это за пропорция? Зададимся двумя немного схожими вопросами:

Какое количество? Сколько? Какой объем? «серой массы» должно быть на старте, чтобы, разделяя ее на «белое» и «черное» получить в точности единицу «проявленного белого» плюс единицу «проявленного черного»?

В какой пропорции белое и черное надо смешивать между собой, чтобы запустить дальнейший самостоятельный процесс развития по единому правилу?

Проверим, что именно это количество и эта пропорция представляют собой Золотую пропорцию, или Золотое сечение, или число «Фи». Сделаем это сначала в одномерном пространстве на отрезке.

Поскольку я проверяю предположение, возьмем серый отрезок длиной «Фи»=1.618… и расщепим его на два отрезка – верхний и нижний, сделав параллельный сдвиг, так чтобы общая длина двух отрезков стала равной двум.

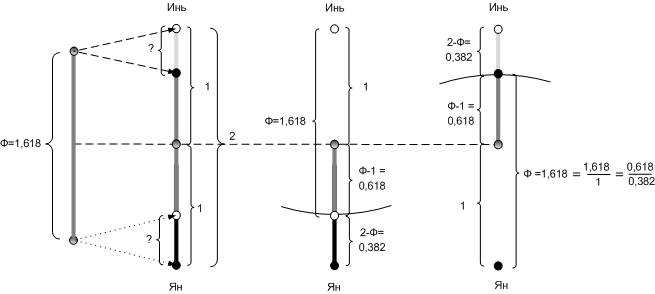
Рис. Золотое сечение отрезка длиной два.

Один отрезок становится верхним и белым, а второй – нижним и черным. Инь и Ян смешиваются в пропорции Золотого сечения. Такой же результат можно получить, взяв отрезок длиной два и отсекая циркулем сначала снизу, а потом сверху диаметр равный «Фи» = 1.618…

Более интересно это проявляется на плоскости. Окружность диаметра «Фи» растет до окружности диаметром два, одновременно порождая две подобные себе пересекающиеся окружности диаметра «Фи» – верхнюю и нижнюю, белую и черную.

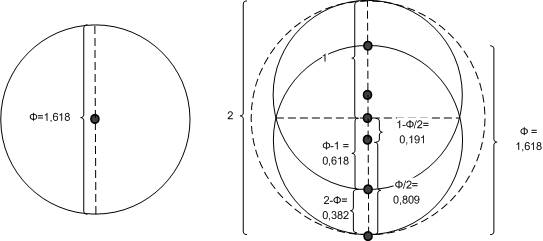
Рис. Золотое сечение окружности диаметром два.

Так вот в чем смысл Золотого Сечения?! Геометрическое Сечение, потому что черный низ частично проникает и влияет на белый верх, а белый верх частично проникает и влияет на черный низ. Эзотерически, это значит, что духовный мир отсекает и частично, проникает и влияет на мир материальный, и наоборот, материальный мир частично проникает и влияет на мир духовный. И все это происходит в строго определенной пропорции. Золотое Сечение, потому что единичный отрезок, например, в нижней проявленной части, чудесным образом оказался разделен в этой же пропорции и к нему может быть продолжен однотипный процесс попеременного сверху и снизу деления-сечения. При этом, получаемые более мелкие отрезки будут относиться друг к другу в одинаковом соотношении, повторяя первичную пропорцию. Взаимное проникновение белого и черного будет уходить в детали на микро уровень, постепенно превращая резкий дискретный переход от белого к черному в более плавный.

Чтобы понять красоту числа Фи, обратимся к музыке и математике. Будем ассоциировать направление вверх с увеличением частоты звука. Разделение отрезка в форме больший внизу, а меньший вверху дает мажорную триаду, или как говорят музыканты, мажорный аккорд, мажорное трезвучие. Разделение отрезка в форме меньший внизу, а больший вверху дает минорную триаду, или минорный аккорд.

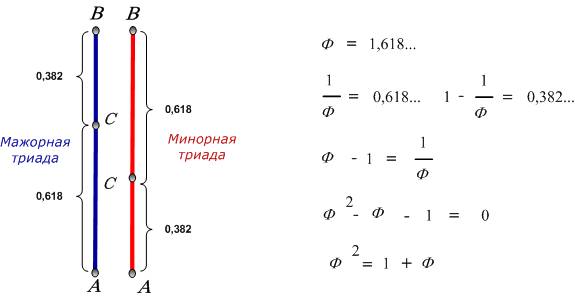
Рис. Мажорная и минорная триады. Свойства числа Фи.

До визуального ощущения красоты мира, остался всего один шаг. Около окружности можно не только вписывать или описывать квадраты. Можно построить прямоугольник, одновременно вписанный сверху и описанный снизу. И здесь нас ждет «Бинго»!!! Это оказался не прямоугольник, а Золотой квадрат со стороной равной «Фи»!!! Так вот откуда великий Леонардо брал пропорции в своих картинах?!

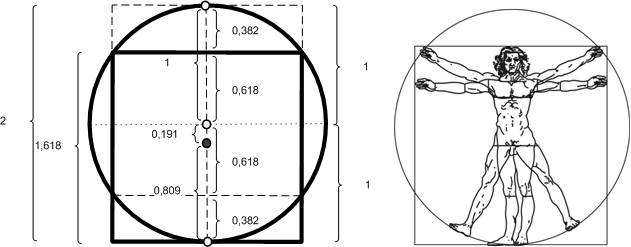
Рис. Золотой квадрат и творения Леонардо Давинчи

Если присмотреться к геометрическому рисунку, вы увидите, что по аналогии с нижним материальным Золотым квадратом, в который идеально вписывается физическое тело человека, в верхней половинке симметрично расположен еще один Золотой квадрат из мира нематериального. Объединение этих квадратов дает вертикальный, а пересечение этих квадратов дает горизонтальный Золотые прямоугольники. Именно в такой пропорции художники размещают холсты своих картин, а архитекторы проектируют фрагменты зданий.

С числом Золотого сечения «Фи» связано много интересных математических формул и физических наблюдений, которым посвящена не одна книга. Здесь же я хотел коснуться лишь одного наблюдения. Площадь и периметр Золотого квадрата можно выразить через параметры окружности, породившей этот квадрат – через числа «Пи» и «Фи».

Это крайне интересно! Числа «Пи» и «Фи» не являются независимыми! Они связаны! И понимание квадратуры круга надо искать, не вписывая и описывая многоугольники в окружность, а изучая свойства Золотого квадрата. Но это понимание, похоже, лежит еще где-то выше за пределами нашего сознания…

Главное, что мы получили – понимание дискретной пропорции в которой взаимодействуют друг с другом две взаимодействующие энергии, пропорцию, дающую правило любому развитию. Однако, углубившись в деление целого на микрочасти, мы не получили понимания как эта пропорция работает в направлении от малого к большому, от простого к сложному, от одной вибрации к сложной волновой гармонии. Для этого еще раз придется вернуться к словам великого восточного мыслителя.

Оглавление книги