Книга: Distributed operating systems

3.4.2. The Transaction Model

3.4.2. The Transaction Model

We will now develop a more precise model of what a transaction is and what its properties are. The system is assumed to consist of some number of independent processes, each of which can fail at random. Communication is normally unreliable in that messages can be lost, but lower levels can use a timeout and retransmission protocol to recover from lost messages. Thus for this discussion we can assume that communication errors are handled transparently by underlying software.

Storage comes in three categories. First we have ordinary RAM memory, which is wiped out when the power fails or a machine crashes. Next we have disk storage, which survives CPU failures but which can be lost in disk head crashes.

Finally, we have stable storage, which is designed to survive anything except major calamities such as floods and earthquakes. Stable storage can be implemented with a pair of ordinary disks, as shown in Fig. 3-15(a). Each block on drive 2 is an exact copy of the corresponding block on drive 1. When a block is updated, first the block on drive 1 is updated and verified, then the same block on drive 2 is done.

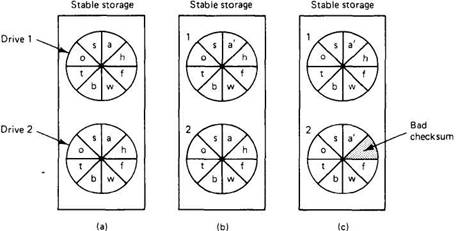
Fig. 3-15. (a) Stable storage. (b) Crash after drive 1 is updated. (c) Bad spot.

Suppose that the system crashes after drive 1 is updated but before drive 2 is updated, as shown in Fig. 3-15(b). Upon recovery, the disk can be compared block for block. Whenever two corresponding blocks differ, it can be assumed that drive 1 is the correct one (because drive 1 is always updated before drive 2), so the new block is copied from drive 1 to drive 2. When the recovery process is complete, both drives will again be identical.

Another potential problem is the spontaneous decay of a block. Dust particles or general wear and tear can give a previously valid block a sudden checksum error, without cause or warning, as shown in Fig. 3-15(c). When such an error is detected, the bad block can be regenerated from the corresponding block on the other drive.

As a consequence of its implementation, stable storage is well suited to applications that require a high degree of fault tolerance, such as atomic transactions. When data are written to stable storage and then read back to check that they have been written correctly, the chance of them subsequently being lost is extremely small.

Programming using transactions requires special primitives that must either be supplied by the operating system or by the language runtime system. Examples are:

1. BEGIN_TRANSACTION: Mark the start of a transaction.

2. END_TRANSACTION: Terminate the transaction and try to commit.

3. ABORT_TRANSACTION: Kill the transaction; restore the old values.

4. READ: Read data from a file (or other object).

5. WRITE: Write data to a file (or other object).

The exact list of primitives depends on what kinds of objects are being used in the transaction. In a mail system, there might be primitives to send, receive, and forward mail. In an accounting system, they might be quite different. READ and WRITE are typical examples, however. Ordinary statements, procedure calls, and so on, are also allowed inside a transaction.

BEGIN_TRANSACTION and END_TRANSACTION are used to delimit the scope of a transaction. The operations between them form the body of the transaction. Either all of them are executed or none are executed. These may be system calls, library procedures, or bracketing statements in a language, depending on the implementation.

Consider, for example, the process of reserving a seat from White Plains, New York, to Malindi, Kenya, in an airline reservation system. One route is White Plains to JFK, JFK to Nairobi, and Nairobi to Malindi. In Fig. 3-16(a) we see reservations for these three separate flights being made as three actions. Now suppose that the first two flights have been reserved but the third one is booked solid. The transaction is aborted and the results of the first two bookings are undone — the airline data base is restored to the value it had before the transaction started [see Fig. 3-16(b)]. It is as though nothing happened.

Fig. 3-16. (a) Transaction to reserve three flights commits. (b) Transaction aborts when third flight is unavailable.

Transactions have four essential properties. Transactions are:

1. Atomic: To the outside world, the transaction happens indivisibly.

2. Consistent: The transaction does not violate system invariants.

3. Isolated: Concurrent transactions do not interfere with each other.

4. Durable: Once a transaction commits, the changes are permanent.

These properties are often referred to by their initial letters, ACID.

The first key property exhibited by all transactions is that they are atomic. This property ensures that each transaction either happens completely, or not at all, and if it happens, it happens in a single indivisible, instantaneous action. While a transaction is in progress, other processes (whether or not they are themselves involved in transactions) cannot see any of the intermediate states.

Suppose, for example, that some file is 10 bytes long when a transaction starts to append to it. If other processes read the file while the transaction is in progress, they see only the original 10 bytes, no matter how many bytes the transaction has appended. If the transaction commits successfully, the file grows instantaneously to its new size at the moment of commitment, with no intermediate states, no matter how many operations it took to get it there.

The second property says that they are consistent. What this means is that if the system has certain invariants that must always hold, if they held before the transaction, they will hold afterward too. For example, in a banking system, a key invariant is the law of conservation of money. After any internal transfer, the amount of money in the bank must be the same as it was before the transfer, but for a brief moment during the transaction, this invariant may be violated. The violation is not visible outside the transaction, however.

The third property says that transactions are isolated or serializable. What it means is that if two or more transactions are running at the same time, to each of them and to other processes, the final result looks as though all transactions ran sequentially in some (system dependent) order.

In Fig. 3-17(a)-(c) we have three transactions that are executed simultaneously by three separate processes. If they were to be run sequentially, the final value of x would be 1,2, or 3, depending which one ran last (x could be a shared variable, a file, or some other kind of object). In Fig. 3-17(d) we see various orders, called schedules, in which they might be interleaved. schedule 1 is actually serialized. In other words, the transactions run strictly sequentially, so it meets the serializability condition by definition. Schedule 2 is not serialized, but is still legal because it results in a value for x that could have been achieved by running the transactions strictly sequentially. The third one is illegal since it sets x to 5, something that no sequential order of the transactions could produce. It is up to the system to ensure that individual operations are interleaved correctly. By allowing the system the freedom to choose any ordering of the operations it wants to — provided that it gets the answer right — we eliminate the need for programmers to do their own mutual exclusion, thus simplifying the programming.

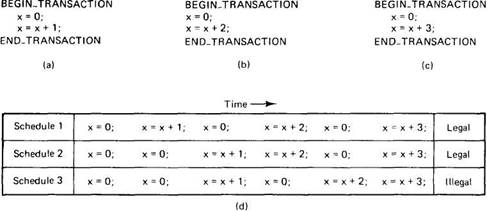
Fig. 3-17. (a)-(c) Three transactions. (d) Possible schedules.

The fourth property says that transactions are durable. It refers to the fact that once a transaction commits, no matter what happens, the transaction goes forward and the results become permanent. No failure after the commit can undo the results or cause them to be lost.

Transactions may contain subtransactions, often called nested transactions. The top-level transaction may fork off children that run in parallel with one another, on different processors, to gain performance or simplify programming.

Each of these children may execute one or more subtransactions, or fork off its own children.

Subtransactions give rise to a subtle, but important, problem. Imagine that a transaction starts several subtransactions in parallel, and one of these commits, making its results visible to the parent transaction. After further computation, the parent aborts, restoring the entire system to the state it had before the top-level transaction started. Consequently, the results of the subtransaction that committed must nevertheless be undone. Thus the permanence referred to above applies only to top-level transactions.

Since transactions can be nested arbitrarily deeply, considerable administration is needed to get everything right. The semantics are clear, however. When any transaction or subtransaction starts, it is conceptually given a private copy of all objects in the entire system for it to manipulate as it wishes. If it aborts, its private universe just vanishes, as if it had never existed. If it commits, its private universe replaces the parent's universe. Thus if a subtransaction commits and then later a new subtransaction is started, the second one sees the results produced by the first one.

Оглавление книги