Книга: Distributed operating systems
3.2.2. A Distributed Algorithm
3.2.2. A Distributed Algorithm
Having a single point of failure is frequently unacceptable, so researchers have looked for distributed mutual exclusion algorithms. Lamport's 1978 paper on clock synchronization presented the first one. Ricart and Agrawala (1981) made it more efficient. In this section we will describe their method.
Ricart and Agrawala's algorithm requires that there be a total ordering of all events in the system. That is, for any pair of events, such as messages, it must be unambiguous which one happened first. Lamport's algorithm presented in Sec. 3.1.1 is one way to achieve this ordering and can be used to provide time-stamps for distributed mutual exclusion.
The algorithm works as follows. When a process wants to enter a critical region, it builds a message containing the name of the critical region it wants to enter, its process number, and the current time. It then sends the message to all other processes, conceptually including itself. The sending of messages is assumed to be reliable; that is, every message is acknowledged. Reliable group communication if available, can be used instead of individual messages.
When a process receives a request message from another process, the action it takes depends on its state with respect to the critical region named in the message. Three cases have to be distinguished:
1. If the receiver is not in the critical region and does not want to enter it, it sends back an OK message to the sender.
2. If the receiver is already in the critical region, it does not reply. Instead, it queues the request.
3. If the receiver wants to enter the critical region but has not yet done so, it compares the timestamp in the incoming message with the one contained in the message that it has sent everyone. The lowest one wins. If the incoming message is lower, the receiver sends back an OK message. If its own message has a lower timestamp, the receiver queues the incoming request and sends nothing.
After sending out requests asking permission to enter a critical region, a process sits back and waits until everyone else has given permission. As soon as all the permissions are in, it may enter the critical region. When it exits the critical region, it sends OK messages to all processes on its queue and deletes them all from the queue.
Let us try to understand why the algorithm works. If there is no conflict, it clearly works. However, suppose that two processes try to enter the same critical region simultaneously, as shown in Fig. 3-9(a).
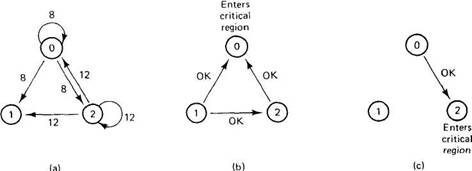
Fig. 3-9. (a) Two processes want to enter the same critical region at the same moment. (b) Process 0 has the lowest timestamp, so it wins. (c) When process 0 is done, it sends an OK also, so 2 can now enter the critical region.
Process 0 sends everyone a request with timestamp 8, while at the same time, process 2 sends everyone a request with timestamp 12. Process 1 is not interested in entering the critical region, so it sends OK to both senders. Processes 0 and 2 both see the conflict and compare timestamps. Process 2 sees that it has lost, so it grants permission to 0 by sending OK. Process 0 now queues the request from 2 for later processing and enters the critical region, as shown in Fig. 3-9(b). When it is finished, it removes the request from 2 from its queue and sends an OK message to process 2, allowing the latter to enter its critical region, as shown in Fig. 3-9(c). The algorithm works because in the case of a conflict, the lowest timestamp wins and everyone agrees on the ordering of the timestamps.
Note that the situation in Fig. 3-9 would have been essentially different if process 2 had sent its message earlier in time so that process 0 had gotten it and granted permission before making its own request. In this case, 2 would have noticed that it itself was in a critical region at the time of the request, and queued it instead of sending a reply.
As with the centralized algorithm discussed above, mutual exclusion is guaranteed without deadlock or starvation. The number of messages required per entry is now 2(n–1), where the total number of processes in the system is n. Best of all, no single point of failure exists.
Unfortunately, the single point of failure has been replaced by n points of failure. If any process crashes, it will fail to respond to requests. This silence will be interpreted (incorrectly) as denial of permission, thus blocking all subsequent attempts by all processes to enter all critical regions. Since the probability of one of the n processes failing is n times as large as a single coordinator failing, we have managed to replace a poor algorithm with one that is n times worse and requires much more network traffic to boot.
The algorithm can be patched up by the same trick that we proposed earlier. When a request comes in, the receiver always sends a reply, either granting or denying permission. Whenever either a request or a reply is lost, the sender times out and keeps trying until either a reply comes back or the sender concludes that the destination is dead. After a request is denied, the sender should block waiting for a subsequent OK message.
Another problem with this algorithm is that either a group communication primitive must be used, or each process must maintain the group membership list itself, including processes entering the group, leaving the group, and crashing. The method works best with small groups of processes that never change their group memberships.
Finally, recall that one of the problems with the centralized algorithm is that making it handle all requests can lead to a bottleneck. In the distributed algorithm, all processes are involved in all decisions concerning entry into critical regions. If one process is unable to handle the load, it is unlikely that forcing everyone to do exactly the same thing in parallel is going to help much.
Various minor improvements are possible to this algorithm. For example, getting permission from everyone to enter a critical region is really overkill. All that is needed is a method to prevent two processes from entering the critical region at the same time. The algorithm can be modified to allow a process to enter a critical region when it has collected permission from a simple majority of the other processes, rather than from all of them. Of course, in this variation, after a process has granted permission to one process to enter a critical region, it cannot grant the same permission to another process until the first one has released that permission. Other improvements are also possible (e.g., Maekawa et al., 1987).
Nevertheless, this algorithm is slower, more complicated, more expensive, and less robust that the original centralized one. Why bother studying it under these conditions? For one thing, it shows that a distributed algorithm is at least possible, something that was not obvious when we started. Also, by pointing out the shortcomings, we may stimulate future theoreticians to try to produce algorithms that are actually useful. Finally, like eating spinach and learning Latin in high school, some things are said to be good for you in some abstract way.




