Книга: Distributed operating systems

4.4. SCHEDULING IN DISTRIBUTED SYSTEMS

4.4. SCHEDULING IN DISTRIBUTED SYSTEMS

There is not really a lot to say about scheduling in a distributed system. Normally, each processor does its own local scheduling (assuming that it has multiple processes running on it), without regard to what the other processors are doing. Usually, this approach works fine. However, when a group of related, heavily interacting processes are all running on different processors, independent scheduling is not always the most efficient way.

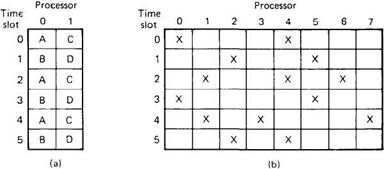
Fig. 4-20. (a) Two jobs running out of phase with each other. (b) Scheduling matrix for eight processors, each with six time slots. The Xs indicated allocated slots.

The basic difficulty can be illustrated by an example in which processes A and B run on one processor and processes C and D run on another. Each processor is timeshared in, say, 100-msec time slices, with A and C running in the even slices and B and D running in the odd ones, as shown in Fig. 4-20(a). Suppose that A sends many messages or makes many remote procedure calls to D. During time slice 0, A starts up and immediately calls D, which unfortunate is not running because it is now C's turn. After 100 msec, process switching takes place, and D gets A's message, carries out the work, and quickly replies. Because B is now running, it will be another 100 msec before A gets the reply and can proceed. The net result is one message exchange every 200 msec. What is needed is a way to ensure that processes that communicate frequently run simultaneously.

Although it is difficult to determine dynamically the interprocess communication patterns, in many cases, a group of related processes will be started off together. For example, it is usually a good bet that the filters in a UNIX pipeline will communicate with each other more than they will with other, previously started processes. Let us assume that processes are created in groups and that intragroup communication is much more prevalent than intergroup communication. Let us assume further that a sufficiently large number of processors is available to handle the largest group, and that each processor is multiprogrammed with N process slots (N–way multiprogramming).

Ousterhout (1982) proposed several algorithms based on a concept he calls co-scheduling, which takes interprocess communication patterns into account while scheduling to ensure that all members of a group run at the same time. The first algorithm uses a conceptual matrix in which each column is the process table for one processor, as shown in Fig. 4-20(b). Thus, column 4 consists of all the processes that run on processor 4. Row 3 is the collection of all processes that are in slot 3 of some processor, starting with the process in slot 3 of processor 0, then the process in slot 3 of processor 1, and so on. The gist of his idea is to have each processor use a round-robin scheduling algorithm with all processors first running the process in slot 0 for a fixed period, then all processors running the process in slot 1 for a fixed period, and so on. A broadcast message could be used to tell each processor when to do process switching, to keep the time slices synchronized.

By putting all the members of a process group in the same slot number, but on different processors, one has the advantage of N –fold parallelism, with a guarantee that all the processes will be run at the same time, to maximize communication throughput. Thus in Fig. 4-20(b), four processes that must communicate should be put into slot 3, on processors 1, 2, 3, and 4 for optimum performance. This scheduling technique can be combined with the hierarchical model of process management used in MICROS by having each department head maintain the matrix for its workers, assigning processes to slots in the matrix and broadcasting time signals.

Ousterhout also described several variations to this basic method to improve performance. One of these breaks the matrix into rows and concatenates the rows to form one long row. With k processors, any k consecutive slots belong to different processors. To allocate a new process group to slots, one lays a window k slots wide over the long row such that the leftmost slot is empty but the slot just outside the left edge of the window is full. If sufficient empty slots are present in the window, the processes are assigned to the empty slots; otherwise, the window is slid to the right and the algorithm repeated. Scheduling is done by starting the window at the left edge and moving rightward by about one window's worth per time slice, taking care not to split groups over windows. Ousterhout's paper discusses these and other methods in more detail and gives some performance results.

Оглавление книги