Книга: Distributed operating systems

4.5.5. Fault Tolerance Using Active Replication

4.5.5. Fault Tolerance Using Active Replication

Active replication is a well-known technique for providing fault tolerance using physical redundancy. It is used in biology (mammals have two eyes, two ears, two lungs, etc.), aircraft (747s have four engines but can fly on three), and sports (multiple referees in case one misses an event). Some authors refer to active replication as the state machine approach.

It has also been used for fault tolerance in electronic circuits for years. Consider, for example, the circuit of Fig. 4-21(a). Here signals pass through devices A, B, and C, in sequence. If one of them is faulty, the final result will probably be wrong.

In Fig. 4-21(b), each device is replicated three times. Following each stage in the circuit is a triplicated voter. Each voter is a circuit that has three inputs and one output. If two or three of the inputs are the same, the output is equal to that input. If all three inputs are different, the output is undefined. This kind of design is known as TMR (Triple Modular Redundancy).

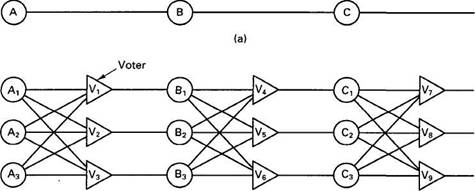
Fig. 4-21. Triple modular redundancy.

Suppose element A₂fails. Each of the voters, V₁, V₂, and V₃ gets two good (identical) inputs and one rogue input, and each of them outputs the correct value to the second stage. In essence, the effect of A₂ failing is completed masked, so that the inputs to B₁, B₂, and B₃ are exactly the same as they would have been had no fault occurred.

Now consider what happens if B₃ and C₁are also faulty, in addition to A₂. These effects are also masked, so the three final outputs are still correct.

At first it may not be obvious why three voters are needed at each stage. After all, one voter could also detect and pass though the majority view. However, a voter is also a component and can also be faulty. Suppose, for example, that V₁malfunctions. The input to B₁will then be wrong, but as long as everything else works, B₂and B₃ will produce the same output and V₄, V₅, and V₆ will all produce the correct result into stage three. A fault in V₁ is effectively no different than a fault in B₁. In both cases B₁produces incorrect output, but in both cases it is voted down later.

Although not all fault-tolerant distributed operating systems use TMR, the technique is very general, and should give a clear feeling for what a fault-tolerant system is, as opposed to a system whose individual components are highly reliable but whose organization is not fault tolerant. Of course, TMR can be applied recursively, for example, to make a chip highly reliable by using TMR inside it, unknown to the designers who use the chip.

Getting back to fault tolerance in general and active replication in particular, in many systems, servers act like big finite-state machines: they accept requests and produce replies. Read requests do not change the state of the server, but write requests do. If each client request is sent to each server, and they all are received and processed in the same order, then after processing each one, all nonfaulty servers will be in exactly the same state and will give the same replies. The client or voter can combine all the results to mask faults.

An important issue is how much replication is needed. The answer depends on the amount of fault tolerance desired. A system is said to be k fault tolerant if it can survive faults in k components and still meet its specifications. If the components, say processors, fail silently, then having k+1 of them is enough to provide k fault tolerance. If k of them simply stop, then the answer from the other one can be used.

On the other hand, if the processors exhibit Byzantine failures, continuing to run when sick and sending out erroneous or random replies, a minimum of 2k+1 processors are needed to achieve k fault tolerance. In the worst case, the k failing processors could accidentally (or even intentionally) generate the same reply. However, the remaining k+1 will also produce the same answer, so the client or voter can just believe the majority.

Of course, in theory it is fine to say that a system is k fault tolerant and just let the k+1 identical replies outvote the k identical replies, but in practice it is hard to imagine circumstances in which one can say with certainty that k processors can fail but k+1 processors cannot fail. Thus even in a fault-tolerant system some kind of statistical analysis may be needed.

An implicit precondition for this finite state machine model to be relevant is that all requests arrive at all servers in the same order, sometimes called the atomic broadcast problem. Actually, this condition can be relaxed slightly, since reads do not matter and some writes may commute, but the general problem remains. One way to make sure that all requests are processed in the same order at all servers is to number them globally. Various protocols have been devised to accomplish this goal. For example, all requests could first be sent to a global number server to get a serial number, but then provision would have to be made for the failure of this server (e.g., by making it internally fault tolerant).

Another possibility is to use Lamport's logical clocks, as described in Chap. 3. If each message sent to a server is tagged with a timestamp, and servers process all requests in timestamp order, all requests will be processed in the same order at all servers. The trouble with this method is that when a server receives a request, it does not know whether any earlier requests are currently under way. In fact, most timestamp solutions suffer from this problem. In short, active replication is not a trivial matter. Schneider (1990) discusses the problems and solutions in some detail.

Оглавление книги