Книга: Почему

Когда вещи изменяются со временем

Когда вещи изменяются со временем

Может ли исчезновение пиратов вызвать повышение температуры в глобальном масштабе? Правда ли, что поедание сыра моцарелла побуждает изучать информационные технологии?[166] В самом деле поставки лимонов в страну снижают количество аварий на дорогах?

На рис. 4.2 (a) показана взаимосвязь между импортом лимонов и количеством погибших в ДТП: чем выше объемы импорта, тем меньше смертельных случаев[167].

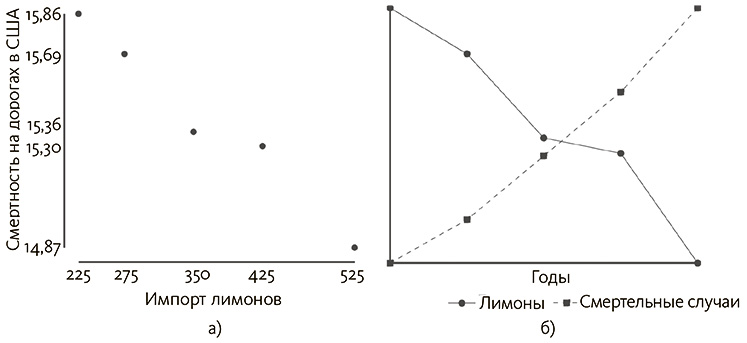
Рис. 4.2. Объемы ввоза лимонов в США (в тоннах) и смертность на дорогах в США [число летальных случаев на 100 человек]: а) как отношение одной переменной к другой и б) как временная функция

Хотя коэффициент корреляции Пирсона для этих данных составляет –0,98, что означает практически абсолютное отрицательное соотношение, никто почему-то до сих пор не предложил увеличить импорт цитрусовых, чтобы снизить количество погибших на дорогах.

А теперь взглянем, что получится на рис. 4.2 (б), если выстроить график данных по импорту и смертельным случаям в виде временной функции. Выходит, импорт со временем неуклонно падает, а смертность за тот же период растет. Данные на рис. 4.2 также представляют динамический ряд в обратном хронологическом порядке. Но мы можем заменить импорт лимонов любым другим динамическим рядом, падающим во времени (долей рынка Internet Explorer; акваторией арктических вод, покрытой льдом; распространением курения в США), и обнаружить точно такую же зависимость.

Причина в том, что подобные временные ряды не стационарны, а это значит, что их свойства – к примеру, средние значения – со временем меняются. Например, дисперсия свойства может модулироваться: средний объем импорта цитрусовых окажется стабильным, а годовые колебания – нет. Спрос на электроэнергию при двух подсчетах в год может проявить нестационарность, поскольку общая потребность будет, вероятнее всего, со временем расти, а тенденции – зависеть от сезонности. С другой стороны, результаты длинных серий подбрасывания монеток считаются стационарными, поскольку вероятность выпадения орлов или решек в каждой временной точке абсолютно одинакова.

Если на длинном временном горизонте наблюдается одинаковый (или абсолютно противоположный) тренд, некоторые ряды будут коррелировать, но это не значит, что один фактор станет причиной другого. Существует и другой метод поиска корреляций без соответствующей каузальной зависимости. Если цена на все акции в определенной группе за конкретный промежуток времени растет, можно обнаружить корреляцию между этими ценами, даже если дневные тренды совершенно отличаются.

В другом примере, который показан на рис. 4.3, количество диагнозов аутизма растет в том же темпе, что и число кофеен Starbucks[168], поскольку и те и другие показатели растут по экспоненте – но то же справедливо и для многих других временных рядов (ВВП, количество веб-страниц и научных статей). Здесь причинно-следственная связь весьма правдоподобна, но это далеко не всегда так, и можно придумать кучу убедительных историй, объясняя различные корреляции динамических рядов. Если бы я вместо этого взяла, скажем, процент домохозяйств[169] с высокоскоростным интернетом, вряд ли можно было найти убедительные свидетельства взаимосвязи, кроме того, что – уж так случилось – оба фактора растут со временем. Хотя кое-кто мог бы и придумать объяснение их взаимоотношений. Но это всего лишь корреляция, которая легко исчезнет, если мы учтем разную степень детализации данных по времени или сделаем поправку на их нестационарность.

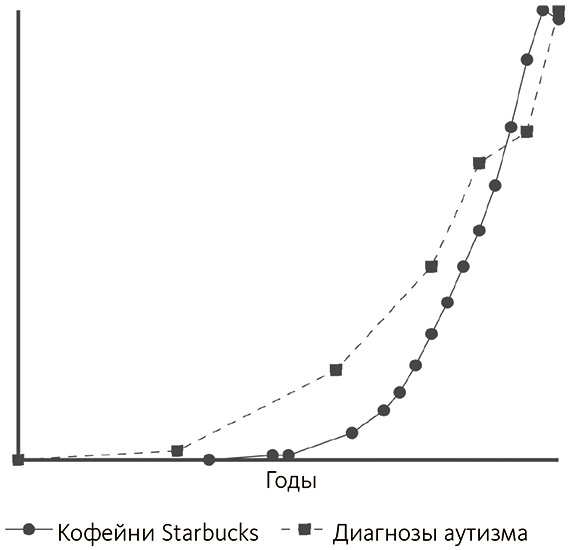
Рис. 4.3. Два нестационарных динамических ряда, которые кажутся коррелирующими только потому, что оба со временем растут по экспоненте

Еще один вид нестационарности – если группа населения, среди которого проводилась выборка, изменяется со временем. В 2013 году Американская кардиологическая ассоциация (American Heart Assosiation, AHA) и Американская коллегия кардиологов (American College of Cardiology, ACC) выпустили новые справочники по борьбе с избытком холестерина вместе с онлайн-калькулятором, чтобы прогнозировать риск инфарктов и инсультов на 10 лет вперед[170]. Однако некоторые исследователи обнаружили, что калькулятор завышает риски на 75–100 %, что может вести к назначению избыточного объема лекарств, потому что рекомендации основаны на уровнях риска для каждого пациента[171].

Калькулятор учитывает такие факторы риска, как диабет, гипертензия и курение, но не берет – и не способен брать – в расчет все возможные моменты, влияющие на уровень риска, к примеру, подробную историю курения в прошлом. Коэффициенты в уравнениях (значимость каждого фактора) оценивались на основании данных, собранных в 1990-х годах, поэтому допущение заключается в том, что и другие свойства этой группы населения совпадут для ее текущего состава. Однако привычки курильщиков и другие важные факторы касательно образа жизни со временем изменились. Согласно анализу Кука и Ридкера (2014), 33 % белого населения на дату начала долгосрочного исследования курили по сравнению с 20 % той же группы на сегодня[172], что дало иной базовый уровень риска и в потенциале привело к переоценке этого фактора[173].

Мы часто говорим о внешней валидности, то есть можно ли экстраполировать некое заключение за пределы исследуемой выборки (подробнее об этом – в главе 7). Но есть и другой тип валидности – по времени.

Внешняя валидность определяет, как то, что мы узнаём в одном месте, способно информировать, что будет происходить в другом: к примеру, смогут ли результаты выборочного контролируемого эксперимента в Европе сказать что-либо об эффективности этого лекарства в США? Со временем также могут наблюдаться изменения в причинно-следственных взаимосвязях (новые законы спровоцируют перемены, влияющие на цену акций) или их силе (если люди начнут читать новости только в Сети, печатные объявления утратят воздействие на умы). Точно так же рекламный агент может выяснить, как конкретная социальная сеть влияет на объем продаж; но если цель, с которой люди пользуются соцсетями, со временем изменится, эта зависимость прекратит существование (например, вместо того чтобы «френдить» только близких друзей, люди начнут массово расширять знакомства).

Используя причинные зависимости, можно сделать косвенное предположение, что вещи, образующие взаимосвязь, со временем проявляют стабильность. Аналогичный сценарий реален, если мы рассматриваем, скажем, данные о повторной госпитализации пациентов на некоем временном отрезке. Возможно, количество рецидивов со временем возросло, и это было вызвано новой политикой или сменой руководства. Но могло случиться так, что население, лечившееся в больнице, также изменилось: к примеру, люди стали менее здоровыми. Получается, политика сама по себе привела к изменениям в населении. Мы узнаем об этом подробнее в главе 9, так как нередко стараемся понять, как причинные зависимости влияют на политику, хотя она сама приносит перемены. В результате первичные причинные зависимости могут прекратиться, и вмешательство окажется неэффективным. Один из примеров – программа сокращения числа учащихся в калифорнийских школах, когда внезапный рост спроса на учителей привел к снижению их профессионального уровня.

Могут также образовываться новые причинно-следственные связи, такие как появление нового канцерогена. Может меняться значение переменных. К примеру, язык постоянно трансформируется, возникают новые слова, а существующие используются иначе (например, слово «плохо» в значении «хорошо»). Или сначала речи политика повышали его рейтинг, поскольку его слова одобрялись обществом, а затем, когда люди перестали с ним соглашаться, его популярность снизилась. В результате прогнозы о повышении рейтингов не сработают, а действия – к примеру, написание новых речей – окажутся неэффективными. А на более коротком временном отрезке зависимость может оказаться истинной, если не учитывать дневные колебания.

Существует несколько стратегий для работы со нестационарными временными рядами. Можно, конечно, проигнорировать нестационарность, однако лучшие подходы используют более короткое время (набор рядов должен обладать стационарностью), если для этого достаточно данных, или же трансформируют временные ряды в стационарные.

В качестве примера нестационарности очень часто берется ситуация, предложенная Эллиотом Собером[174], [175], – зависимость между уровнем воды в Венецианской лагуне и ценами на хлеб в Англии, которые видимым образом коррелируют и со временем растут. Действительно, если взять данные Собера из этого примера с рис. 4.4 (а) (единицы переменных не приводятся), корреляция Пирсона для переменных составляет 0,8204. Хотя два временных ряда всегда растут, точный размер этого роста каждый год варьируется. Что мы действительно хотим понять – как эти изменения соотносятся.

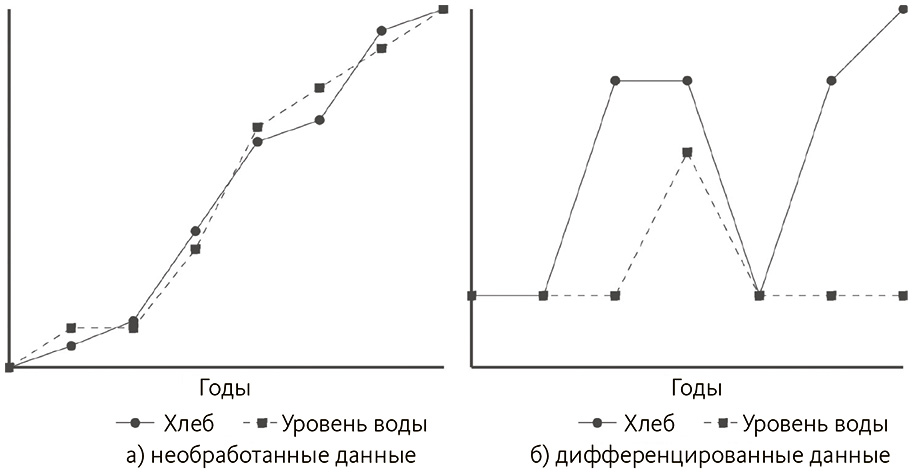
Рис. 4.4. Уровень моря и цены на хлеб

Простейший подход заключается в изучении различий, а не голых фактов. Иными словами, насколько сильно увеличивается уровень моря или цены на хлеб относительно измерений предыдущего года?

Если взять изменения по годам, как показано на рис. 4.4 (б), корреляция падает до 0,4714.

Такой подход называется дифференцированием (что буквально означает вычисление разности между последовательными точками данных): это простейший способ превратить временной ряд в стационарный.

Даже если два временных ряда показывают одинаковые долгосрочные тренды (например, неуклонный прирост), дифференцированные данные могут уже не коррелировать, если разнятся дневные или годовые колебания. В целом одно только дифференцирование не гарантирует стационарность измененного временного ряда; требуются более сложные трансформации данных[176].

Это одна из причин, по которым работа с фондовым рынком обычно использует прибыли (изменение цены), а не фактические ценовые данные. Обратите внимание: именно здесь обнаружилась связь с лимонами и смертностью в ДТП, и именно поэтому можно выявить одинаковые зависимости для многих пар динамических рядов. Если общие тренды аналогичны и значимы, они обеспечивают основную часть измерений корреляции, доминируя над любыми различиями краткосрочных трендов, которые могут совершенно не коррелировать[177].

Оглавление книги