Книга: Фундаментальные алгоритмы и структуры данных в Delphi

Удаление из красно-черного дерева

Удаление из красно-черного дерева

По сравнению со вставкой, удаление из красно-черного дерева сопряжено с множеством особых случаев и его может быть трудно отследить.

Как обычно, при использовании деревьев бинарного поиска, начнем с поиска узла, который требуется удалить. Как и ранее, возможны три начальных случая: узел не имеет дочерних узлов (или, применяя терминологию, принятую в красно-черных деревьях, оба его дочерних узла являются внешними);

узел имеет один реальный дочерний узел и один внешний дочерний узел;

и, наконец, узел имеет два реальных дочерних узла. Удаление узла выполняется так же, как это делалось в стандартном неокрашенном дереве бинарного поиска.

Теперь рассмотрим эти три случая с точки зрения красно-черных деревьев. Первый случай - узел с двумя внешними дочерними узлами (т.е. с нулевыми связями). В соответствии с правилом 1, эти два дочерних узла считаются черными. Однако узел, который нужно удалить, может быть красным или черным. Предположим, что он красный. Удаляя его, мы заменяем дочернюю связь родительского узла нулевым указателем - иначе говоря, внешним черным узлом. Однако мы не изменили количество черных узлов от нового внешнего узла до корневого узла, по сравнению с существовавшими до этого двумя путями. Следовательно, правило 2 по-прежнему выполняется. Очевидно, что правило 3 также не нарушается (мы удаляем красный узел, поэтому никакие проблемы в отношении соблюдения этого правила не возникают). Таким образом, после удаления бинарное дерево остается красно-черным. Эта возможность представлена первым преобразованием на рис. 8.10.

А как насчет второй возможности (когда удаляемый узел окрашен в черный цвет)? Что ж, в этом случае правило 2, сформулированное для черных узлов, неизбежно нарушается. Количество черных узлов в пути до корневого узла уменьшается на 1. Возникающая в результате такого преобразования проблема проиллюстрирована на нижней части рисунка 8.10. Мысленно заложим в этом месте закладку и рассмотрим другие случаи.

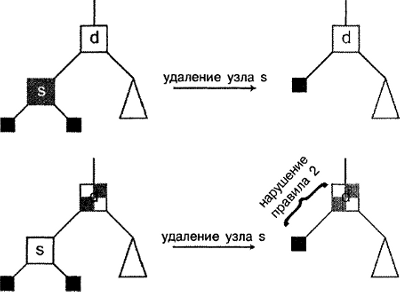
Рисунок 8.10. Удаление узла, имеющего два внешних дочерних узла

Второй случай удаления - удаление узла, который имеет один реальный дочерний узел и один внешний дочерний узел. Предположим, что удаляемый узел является красным. Его единственный реальный дочерний узел будет черным. Можно удалить узел и заменить его единственным дочерним узлом. Это не приведет к нарушению правила 2, - в конечном счете, мы удаляем красный узел, - а правило 3 в данном случае не затрагивается, следовательно, дерево остается красно-черным. Этот случай представлен первым преобразованием на рис. 8.11.

Теперь предположим, что удаляемый узел является черным. Единственный дочерний узел может быть красным или черным. Предположим, что он красный. Правило 2 неизбежно нарушается, поскольку мы удаляем черный узел, а правило 3 может быть нарушено, так как новый родительский узел красного дочернего узла может также оказаться красным. Однако этот случай достаточно прост: нужно просто перекрасить красный дочерний узел в черный цвет при перемещении его вверх для замещения удаленного узла. В результате этого простого действия мы снова добиваемся выполнения правила 2, а правило 3 в данном случае не затрагивается. Дерево снова становится красно-черным. Тот случай представлен вторым преобразованием, показанным на рис. 8.11.

Однако случай, когда единственный дочерний узел является черным, сложнее третье преобразование (на рис. 8.11). Что ж, запомним о существовании этой проблемы и рассмотрим третий, он же и последний, случай удаления.

В действительности заключительный случай удаления из дерева бинарного поиска не отличается от двух уже рассмотренных, поскольку, если помните, мы меняем местами узел, который нужно было бы удалить, с наибольшим узлом из левого дочернего дерева, а затем удаляем этот второй узел вместо первого. Этот второй узел будет соответствовать либо первому, либо второму случаю удаления, поэтому две проблемы, решение которых мы отложили, придется решать раньше, чем мы полагали.

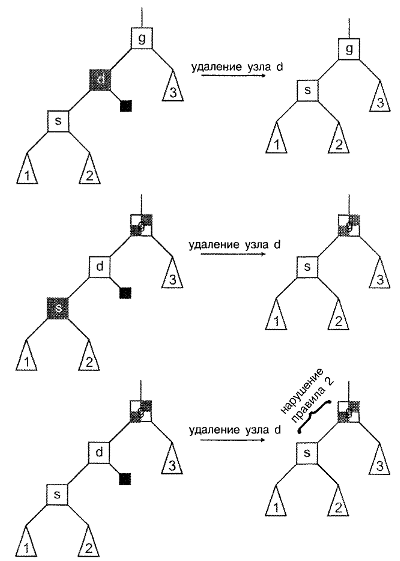
Рисунок 8.11.

Удаление узла, который имеет один внутренний и один внешний дочерний узел

Кратко напомним, в чем они состоят. Удаляемый узел имеет, по меньшей мере, один внешний узел. Если удаляемый узел красный, то его второй дочерний узел должен быть черным (конечно, он может быть внешним узлом, поскольку внешние узлы автоматически окрашиваются в черный цвет). Можно удалить узел, заменить его этим вторым дочерним узлом, и в результате дерево останется красно-черным. Если удаляемый узел является черным и имеет один красный внутренний дочерний узел, то можно удалить узел и заменить его дочерним узлом, окрасив его в черный цвет.

Однако если удаляемый узел черный и имеет, по меньшей мере, один внешний дочерний узел, а другой дочерний узел либо черный, либо внешний, то мы сталкиваемся с двумя ранее описанными проблемами. Повышение ранга дочернего узла в результате удаления приводит к нарушению правила 2 (назовем этот узел нарушающим узлом). Эти случаи представлены последними преобразованиями, изображенными на рисунках 8.10 и 8.11.

Попытаемся свести оба случая к одному. Мы должны принимать во внимание родительский и братский узлы нарушающего узла и два дочерних узла братского узла (узлы-племянники). Обратите внимание, что можно принять наличие у братского узла двух дочерних узлов (т.е. считать, что братский узел не является внешним). Почему? Рассмотрим исходное дерево. Оно было красно-черным. Следовательно, все пути, проходящие через удаленный и родительский узлы, имели то же количество черных узлов, что и пути, проходящие через братский и родительский узлы. Поскольку мы предполагаем, что родительский узел черный, а удаленный узел и заменивший его дочерний узел также были черными, то и все пути, проходящие через братский узел, должны содержать, по меньшей мере, два черных узла. Отсюда следует, что, как минимум, братский узел является черным и имеет два черных дочерних узла.

Как бы там ни было, рассмотрим братский узел. Последующие рассуждения упростятся, если принять, что братский узел является черным. Если это не так, нужно перекрасить родительский узел в красный цвет, а братский - в черный, после чего повернуть родительский узел и повысить ранг братского узла. Результирующее дерево будет красно-черным, если не обращать внимания на исходный нарушающий узел, но в нем братский узел гарантированно является черным. Таким образом, в дальнейшем будем считать, что братский узел окрашен в черный цвет. (Обратите внимание, что если бы братский узел был красным, то его дочерние узлы должны были быть черными и, более того, чтобы правило 2 изначально выполнялось, они должны были бы иметь собственные дочерние узлы. Следовательно, это преобразование сохраняет существование братского узла с дочерними узлами и красно-черное состояние дерева.)

Вначале необходимо рассмотреть случай, когда нарушающий узел имеет черный родительский узел и два черных узла-племянника. Перекрашивание братского узла в красный цвет приводит к перемещению проблемной области вверх к родительскому узлу, и можно просто повторить весь алгоритм применительно к этому узлу, как к нарушающему правило. Эта возможность показана на рис. 8.12.

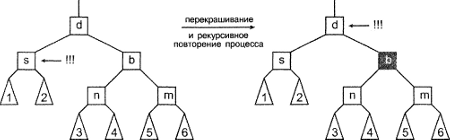
Рисунок 8.12. Балансировка после удаления: первый случай

Второй возможный случай - существование красного родительского узла и двух черных узлов-племянников. Этот случай даже проще предыдущего: нужно перекрасить родительский узел в черный цвет, а братский - в красный. Путь, проходящий через нарушающий узел, снова имеет требуемое количество черных узлов (тем самым удовлетворяя правило 2). Это же можно сказать и по поводу пути, проходящего через братский узел (правило 2 снова выполняется). Только что окрашенный в красный цвет узел имеет черный родительский узел, следовательно, правило 3 не нарушается. Стало быть, мы снова получаем красно-черное дерево. Этот случай показан на рис. 8.13.

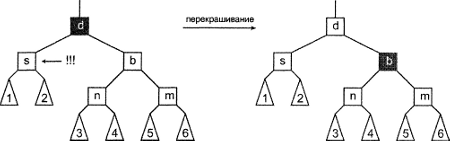
Рисунок 8.13. Балансировка после удаления: второй случай

Теперь предположим, что противоположный по отношению к нарушающему узлу узел-племянник является красным. (Иначе говоря, если нарушающий узел -это левый дочерний узел родительского узла, речь идет о правом узле-племяннике, а если нарушающий узел - правый дочерний узел, речь идет о левом узле-племяннике.) Перекрасим этот узел-племянник в черный цвет. Окрасим братский узел в цвет родительского узла (первоначальный цвет родительского узла не имеет значения), а родительский узел - в черный цвет. Затем повернем родительский узел и повысим ранг братского узла. Тщательно проанализируем эту ситуацию, глядя на рис. 8.14. Вначале проверим выполнение правила 3: очевидно, что мы не ввели никаких новых красных узлов, следовательно, можно быть уверенным, что это правило выполняется. Теперь рассмотрим выполнение правила 2. Все пути, проходящие через нарушающий узел, содержат дополнительный черный узел, что ведет к устранению проблемы, возникшей в результате удаления исходного узла. Все пути, проходящие через дочерние деревья 5 и 6, также содержат то же количество черных узлов, что и ранее. Следовательно, во всех случаях правило 2 выполняется, и результирующее дерево снова является красно-черным.

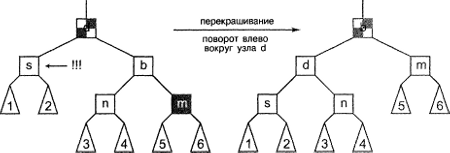
Рисунок 8.14. Балансировка после удаления: третий случай

Теперь рассмотрим последний случай. Предположим, что противоположный узел-племянник окрашен в черный цвет, но второй узел этой же степени родства является красным. На этот раз нужно выполнить спаренный двусторонний поворот. Вначале мы окрашиваем узел-племянник в цвет родительского узла (как и в предыдущем случае, первоначальный цвет родительского узла значения не имеет), а затем перекрашиваем родительский узел в черный цвет. Далее мы поворачиваем братский узел, чтобы повысить ранг узла-племянника, а затем поворачиваем родительский узел, чтобы снова повысить ранг узла-племянника. Это преобразование показано на рис. 8.15. В любом случае это не ведет к непреднамеренному нарушению правила 3: мы не ввели никаких новых красных узлов. Теперь что касается правила 2 - все пути, проходящие через нарушающий узел, содержат один дополнительный черный узел, следовательно, ранее описанная проблема устранена. Все пути, проходящие через дочернее дерево 3, по-прежнему содержат одинаковое количество черных узлов. Аналогично, во всех путях, проходящих через дочерние деревья 4, 5 и 6, не был вставлен или удален какой-либо дополнительный черный узел, следовательно, правило 3 по-прежнему выполняется. Дерево снова оказывается красно-черным.

Если нарушающий узел удается переместить до позиции корневого узла, создается предельная ситуация. В этом случае нарушающий узел не имеет родительского узла и, следовательно, не может иметь братский узел. При этом нарушающий узел больше не представляет проблемы.

Конечно, все рассмотренные случаи имеют аналоги, представляющие их зеркальные отражения, но при этом анализ каждого из случаев удаления остается тем же. При написании кода подпрограммы удаления нужно будет убедиться, что мы правильно отразили как левые, так и правые варианты расположения узлов.

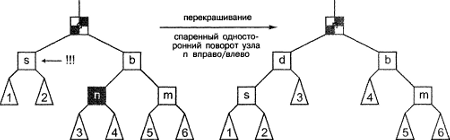
Рисунок 8.15. Балансировка после удаления: заключительный случай

Итак, мы рассмотрели все возможности. При этом использовались два рекурсивных шага или, точнее, два шага, которые требовали дальнейших усилий по балансировке. Первый - когда братский узел был красным, и его нужно было сделать черным. Второй - когда родительский, братский и узлы-племянники были черными. Существовали еще три случая: родительский узел был красным, а братский узел и узлы-племянники были черными;

братский узел был черным, а дальний узел-племянник красным (цвет родительского узла и ближайшего узла-племянника "не имели значения");

и, наконец, случай, когда братский узел был черным, дальний узел-племянник черным, а ближайший узел-племянник красным. Если вы еще раз взглянете на рисунки 8.12, 8.13, 8.14 и 8.15, то убедитесь, что мы рассмотрели все варианты.

Опуская математические выкладки, отметим, что алгоритм удаления из красно-черного дерева является алгоритмом типа O(log(n)), хотя постоянный коэффициент времени больше, чем в случае простого бинарного дерева.

Операция удаления узла из красно-черного дерева реализуется с помощью кода, представленного в листинге 8.25.

Листинг 8.25. Удаление из красно-черного дерева

procedure TtdRedBlackTree.Delete(aItem : pointer);

var

Node : PtdBinTreeNode;

Dad : PtdBinTreeNode;

Child : PtdBinTreeNode;

Brother : PtdBinTreeNode;

FarNephew : PtdBinTreeNode;

NearNephew : PtdBinTreeNode;

IsBalanced : boolean;

ChildType : TtdChildType;

begin

{выполнить поиск узла, который нужно удалить; этот узел будет иметь единственный дочерний узел}

Node := bstFindNodeToDelete(aItem);

{если узел красный или является корневым, его можно безнаказанно удалить}

if (Node^.btColor = rbRed) or (Node = FBinTree.Root) then begin

FBinTree.Delete(Node);

dec(FCount);

Exit;

end;

{если единственный дочерний узел является красным, перекрасить его в черный цвет и удалить узел}

if (Node^.btChild[ctLeft] =nil) then

Child := Node^.btChild[ctRight] else

Child :=Node^.btChild[ctLeft];

if IsRed(Child) then begin

Child^.btColor :=rbBlack;

FBinTree.Delete(Node);

dec(FCount);

Exit;

end;

{на этом этапе узел, который нужно удалить, - узел Node; он является черным и известно, что дочерний узел Child, который его заменит, является черным (а также может быть нулевым!) и что существует родительский узел узла Node (который вскоре станет родительским узлом узла Child); братский узел узла Node также существует в соответствии с правилом, сформулированным для черных узлов}

{если узел Child является нулевым, необходимо несколько упростить выполнение цикла и определить родительский и братский узлы и определить, является ли узел Node левым дочерним узлом}

if (Child = nil) then begin

Dad := Node^.btParent;

if (Node = Dad^.btChild[ctLeft]) then begin

ChildType :=ctLeft;

Brother := Dad^.btChild[ctRight];

end

else begin

ChildType :=ctRight;

Brother := Dad^.btChild[ctLeft];

end;

end

else begin

{следующие три строки предназначены просто для введения в заблуждение компилятора и предотвращения вывода ряда ложных предупреждений}

Dad := nil;

Brother := nil;

ChildType :=ctLeft;

end;

{удалить узел — он больше не нужен}

FBinTree.Delete(Node);

dec(FCount);

Node := Child;

{циклически применять алгоритмы балансировки при удалении из красно-черного дерева до тех пор, пока дерево не окажется сбалансированным}

repeat

{предположим, что дерево сбалансировано}

IsBalanced := true;

{если узел является корневым, балансировка выполнена, поэтому предположим, что это не так}

if (Node <> FBinTree.Root) then begin

{получить родительский и братский узлы}

if (Node <> nil) then begin

Dad := Node^.btParent;

if (Node = Dad^.btChild[ctLeft]) then begin

ChildType := ctLeft;

Brother := Dad^.btChild[ctRight];

end

else begin

ChildType := ctRight;

Brother := Dad^.btChild[ctLeft];

end;

end;

{нам требуется наличие черного братского узла, поэтому если в настоящий момент братский узел окрашен в красный цвет, окрасить родительский узел в красный цвет, братский узел в черный цвет и повысить ранг братского узла; затем снова повторить цикл}

if (Brother^.btColor = rbRed) then begin

Dad^.btColor := rbRed;

Brother^.btColor :=rbBlack;

rbtPromote(Brother);

IsBalanced := false;

end

{ в противном случае братский узел является черным}

else begin

{получить узлы-племянники, помеченные как дальний и ближний}

if (ChildType = ctLeft) then begin

FarNephew := Brother^.btChild[ctRight];

NearNephew := Brother^.btChild[ctLeft];

end

else begin

FarNephew := Brother^.btChild[ctLeft];

NearNephew := Brother^.btChild[ctRight];

end;

{если дальний узел-племянник является красным (обратите внимание, что он может быть нулевым), окрасить его в черный цвет, братский узел в цвет родительского узла, а родительский узел в красный цвет, а затем повысить ранг братского узла; задача выполнена}

if IsRed( FarNephew) then begin

FarNephew^.btColor :=rbBlack;

Brother^.btColor := Dad^.btColor;

Dad^.btColor :=rbBlack;

rbtPromote(Brother);

end

{в противном случае дальний узел-племянник является черным}

else begin

{если ближний узел-племянник является красным (обратите внимание, что он может быть нулевым), окрасить его в цвет родительского узла, родительский узел в черный цвет и повысить ранг узла-племянника посредством спаренного двустороннего поворота; в этом случае задача выполнена}

if isRed(NearNephew) then begin

NearNephew^.btColor := Dad^.btColor;

Dad^.btColor :=rbBlack;

rbtPromote(rbtPromote(NearNephew));

end

{в противном случае ближний узел-племянник является также черным}

else begin

{если родительский узел красный, окрасить его в черный цвет, а братский узел в красный, в результате чего задача будет выполнена}

if (Dad^.btColor = rbRed) then begin

Dad^.btColor :=rbBlack;

Brother^.btColor := rbRed;

end

{в противном случае родительский узел красный: окрасить братский узел в красный цвет и начать балансировку с родительского узла}

else begin

Brother^.btColor := rbRed;

Node := Dad;

IsBalanced := false;

end;

end;

end;

end;

end;

until IsBalanced;

end;

За исключением перекрытых методов Insert и Delete, класс TtdRedBlackTree не представляет особого интереса. Код интерфейса и дополнительного внутреннего метода, выполняющего повышение ранга узла, приведен в листинге 8.26.

Листинг 8.26. Класс TtdRedBlack и метод повышения ранга узла

type

TtdRedBlackTree = class(TtdBinarySearchTree) private protected

function rbtPromote(aNode : PtdBinTreeNode): PtdBinTreeNode;

public

procedure Delete(aItem : pointer); override;

procedure Insert(aItem : pointer); override;

end;

function TtdRedBlackTree.rbtPromote(aNode : PtdBinTreeNode): PtdBinTreeNode;

var

Parent : PtdBinTreeNode;

begin

{пометить родительский узел узла, ранг которого повышается}

Parent := aNode^.btParent;

{в обоих случаях существует 6 связей, которые необходимо разорвать и перестроить: связь узла с его дочерним узлом и противоположная связь; связь узла с его родительским узлом и противоположная связь; и связь родительского узла с его родительским узлом и противоположная связь; обратите внимание, что дочерний узел данного узла может быть нулевым}

{повысить ранг левого дочернего узла, т.е. выполнить поворот родительского узла вправо}

if (Parent^.btChild[ctLeft] = aNode) then begin

Parent^.btChild[ctLeft] := aNode^.btChild[ctRight];

if (Parent^.btChild[ctLeft]<> nil) then

Parent^.btChild[ctLeft]^.btParent := Parent;

aNode^.btParent := Parent^.btParent;

if (aNode^.btParent^.btChild[ctLeft] = Parent) then

aNode^.btParent^.btChild[ctLeft] := anode

else

aNode^.btParent^.btChild[ctRight J := aNode;

aNode^.btChild[ctRight] := Parent;

Parent^.btParent := aNode;

end

{повысить ранг правого дочернего узла, т.е. выполнить поворот родительского узла влево}

else begin

Parent^.btChild[ctRight] := aNode^.btChild[ctLeft];

if (Parent^.btChild[ctRight]<> nil) then

Parent^.btChild[ctRight]^.btParent := Parent;

aNode^.btParent := Parent^.btParent;

if (aNode^.btParent^.btChild[ctLeft] = Parent) then

aNode^.btParent^.btChild[ctLeft] := anode else

aNode^.btParent^.btChild[ctRight] := aNode;

aNode^.btChild[ctLeft] := Parent;

Parent^.btParent := aNode;

end;

{вернуть узел, ранг которого был повышен}

Result := aNode;

end;

Исходный код класса TtdRedBlackTree можно найти на Web-сайте издательства, в разделе материалов. После выгрузки материалов отыщите среди них файл TDBinTre.pas.

Оглавление книги