Книга: Базы данных: конспект лекций
4. Варианты операций соединения
4. Варианты операций соединения
Используя как основу рассмотренные ранее унарные операции выборки, проекции, переименования и бинарные операции объединения, пересечения, разности, декартова произведения и естественного соединения (все они в общем случае называются операциями соединения), мы можем ввести новые операции, выведенные с помощью перечисленных понятий и определений. Подобная деятельность называется составлением вариантов операций соединения.
Первым таким вариантом операций соединения является операция внутреннего соединения по заданному условию соединения.
Операция внутреннего соединения по какому-то определенному условию определяется как производная операция от операций декартового произведения и выборки.
Запишем формульное определение этой операции:
r1(S1) ? Pr2(S2) = ? <P> (r1 ? r2), S1 ? S2 = ?;
Здесь P = P <S1 ? S2> – условие, накладываемое на объединение двух схем исходных отношений-операндов. Именно по этому условию и происходит отбор кортежей из отношений r1 и r2 в результирующее отношение.
Следует отметить, что операция внутреннего соединения может применяться к отношениям с разными схемами отношений. Эти схемы могут быть любыми, но они ни в коем случае не должны пересекаться.
Кортежи исходных отношений-операндов, попавшие в результат операции внутреннего соединения, называются соединимыми кортежами.
Для наглядного иллюстрирования работы операции внутреннего соединения, приведем следующий пример.
Пусть нам даны два отношения r1(S1) и r2(S2) с различными схемами отношения:
r1(S1):
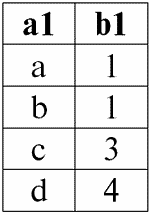
r2(S2):
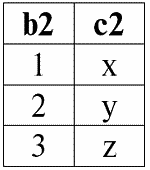
Следующая таблица даст результат применения операции внутреннего соединения по условию P = (b1 = b2).
r1(S1) ? Pr2(S2):
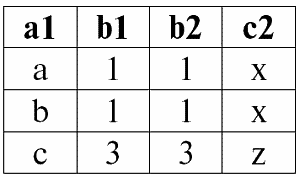
Итак, мы видим, что действительно «слипание» двух таблиц, представляющих отношения, произошло именно по тем кортежам, в которых выполняется условие операции внутреннего соединения P = (b1 = b2).
Теперь на основании уже введенной операции внутреннего соединения мы можем ввести операцию левого внешнего соединения и правого внешнего соединения. Поясним.
Результатом операции левое внешнее соединение является результат внутреннего соединения, пополненный несоединимыми кортежами левого исходного отношения-операнда. Аналогично результат операции правого внешнего соединения определяется как результат операции внутреннего соединения, пополненный несоединимыми кортежами стоящего справа исходного отношения-операнда.
Вопрос, чем же пополняются результирующие отношения операций левого и правого внешнего соединения, вполне ожидаем. Кортежи одного отношения-операнда дополняются на схеме другого отношения-операнда Null-значениями.
Стоит заметить, что введенные таким образом операции левого и правого внешнего соединения являются производными операциями от операции внутреннего соединения.
Чтобы записать общие формулы для операций левого и правого внешнего соединений, проведем некоторые дополнительные построения.
Пусть нам даны два отношения r1(S1) и r2(S2) с различными схемами отношений S1 и S2, не пересекающимися друг с другом.
Так как мы уже оговаривали, что операции левого и правого внутреннего соединения являются производными, то мы можем получить следующие вспомогательные формулы для определения операции левого внешнего соединения:
1) r3 (S2 ? S1) ? r1(S1) ? Pr2(S2);
r3 (S2 ? S1) — это просто результат внутреннего соединения отношений r1(S1) и r2(S2). Левое внешнее соединение является производной операцией именно от операции внутреннего соединения, поэтому мы и начинаем наши построения с нее;
2) r4(S1) ? r3(S2?S1) [S1];
Таким образом, с помощью унарной операции проекции, мы выделили все соединимые кортежи левого исходного отношения-операнда r1(S1). Результат обозначили r4(S1) для удобства применения;
3) r5 (S1) ? r1(S1) r4(S1);
Здесь r1(S1) — все кортежи левого исходного отношения-операнда, а r4(S1) – его же кортежи, только соединимые. Таким образом, при помощи бинарной операции разности, в отношении r5(S1) у нас получились все несоединимые кортежи левого отношения-операнда;
4) r6(S2)? {?(S2)};
{?(S2)} — это новое отношение со схемой (S2), содержащее всего один кортеж, причем составленный из Null-значений. Для удобства мы обозначили это отношение r6(S2);
5) r7 (S2 ? S1) ? r5(S1) ? r6(S2);
Здесь мы взяли полученные в пункте три, несоединимые кортежи левого отношения-операнда (r5(S1)) и дополнили их на схеме второго отношения-операнда S2 Null-значениями, т. е. декартово умножили отношение, состоящее из этих самых несоединимых кортежей на отношение r6(S2), определенное в пункте четыре;
6) r1(S1) ?? P r2(S2) ? (r1 ? Pr2) ? r7 (S2 ? S1);
Это и есть левое внешнее соединение, полученное, как можно видеть, объединением декартового произведения исходных отношений-операндов r1 и r2 и отношения r7 (S2? S1), определенного в пункте пятом.
Теперь у нас имеются все необходимые выкладки для определения не только операции левого внешнего соединения, но по аналогии и для определения операции правого внешнего соединения. Итак:
1) операция левого внешнего соединения в строгом формулярном виде выглядит следующим образом:
r1(S1) ?? Pr2(S2) ? (r1 ? Pr2) ? [(r1 (r1 ? Pr2) [S1]) ? {?(S2)}];
2) операция правого внешнего соединения определяется подобным образом операции левого внешнего соединения и имеет следующий вид:
r1(S1) ?? Pr2(S2) ? (r1 ? Pr2) ? [(r2 (r1 ? Pr2) [S2]) ? {?(S1)}];
Эти две производные операции имеют всего два свойства, достойные упоминания.
1. Свойство коммутативности:
1) для операции левого внешнего соединения:
r1(S1) ?? Pr2(S2) ? r2(S2) ?? Pr1(S1);
2) для операции правого внешнего соединения:
r1(S1) ?? Pr2(S2) ? r2(S2) ?? Pr1(S1)
Итак, мы видим, что свойство коммутативности не выполняется для этих операций в общем виде, но при этом операции левого и правого внешнего соединения взаимно обратны друг другу, т. е. выполняется:
1) для операции левого внешнего соединения:
r1(S1) ?? Pr2(S2) = r2(S2) ?? Pr1(S1);
2) для операции правого внешнего соединения:
r1(S1) ?? Pr2(S2) = r2(S2) ?? Pr1(S1).
2. Основным свойством операций левого и правого внешнего соединения является то, что они позволяют восстановить исходное отношение-операнд по конечному результату той или иной операции соединения, т. е. выполняются:
1) для операции левого внешнего соединения:
r1(S1) = (r1 ?? Pr2) [S1];
2) для операции правого внешнего соединения:
r2(S2) = (r1 ?? Pr2) [S2].
Таким образом, мы видим, что первое исходное отношение-операнд можно восстановить из результата операции левого правого соединения, а если конкретнее, то применением к результату этого соединения (r1 ? r2) унарной операции проекции на схему S1, [S1].
И аналогично второе исходное отношение-операнд можно восстановить применением к результату операции правого внешнего соединения (r1 ? r2) унарной операции проекции на схему отношения S2.
Приведем пример для более подробного рассмотрения работы операций левого и правого внешних соединений. Введем уже знакомые нам отношения r1(S1) и r2(S2) с различными схемами отношения:
r1(S1):
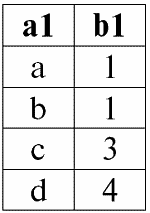
r2(S2):
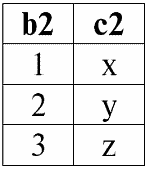
Несоединимый кортеж левого отношения-операнда r2(S2) – это кортеж {d, 4}. Следуя определению, именно им следует дополнить результат внутреннего соединения двух исходных отношений-операндов.
Условие внутреннего соединения отношений r1(S1) и r2(S2) также оставим прежнее: P = (b1 = b2). Тогда результатом операции левого внешнего соединения будет следующая таблица:
r1(S1) ?? Pr2(S2):
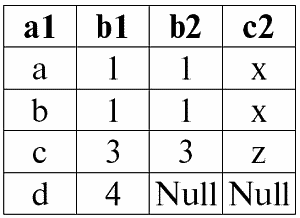
Действительно, как мы можем видеть, в результате воздействия операции левого внешнего соединения, произошло пополнение результата операции внутреннего соединения несоединимыми кортежами левого, т. е. в нашем случае первого отношения-операнда. Пополнение кортежа на схеме второго (правого) исходного отношения-операнда по определению произошло при помощи Null-значений.
И аналогично результатом правого внешнего соединения по тому же, что и раньше, условию P = (b1 = b2) исходных отношений-операндов r1(S1) и r2(S2) является следующая таблица:
r1(S1) ?? Pr2(S2):
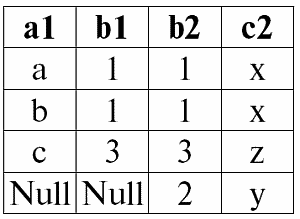
Действительно, в этом случае пополнять результат операции внутреннего соединения следует несоединимыми кортежами правого, в нашем случае второго исходного отношения-операнда. Такой кортеж, как не трудно видеть, во втором отношении r2(S2) один, а именно {2, y}. Далее действуем по определению операции правого внешнего соединения, дополняем кортеж первого (левого) операнда на схеме первого операнда Null-значениями.
И, наконец, рассмотрим третий вариант приведенных ранее операций соединения.
Операция полного внешнего соединения. Эту операцию вполне можно рассматривать не только как операцию, производную от операций внутреннего соединения, но и как объединение операций левого и правого внешнего соединения.
Операция полного внешнего соединения определяется как результат пополнения того же самого внутреннего соединения (как и в случае определения левого и правого внешних соединений) несоединимыми кортежами одновременно и левого, и правого исходных отношений-операндов. Исходя из этого определения дадим формулярный вид этого определения:
r1(S1) ?? Pr2(S2) = (r1 ?? Pr2) ? ( r1 ?? Pr2);
У операции полного внешнего соединения также имеется свойство, сходное с аналогичным свойством операций левого и правого внешних соединений. Только за счет изначальной взаимно-обратной природы операции полного внешнего соединения (ведь она была определена как объединение операций левого и правого внешних соединений) для нее выполняется свойство коммутативности:
r1(S1) ?? Pr2(S2)= r2(S2) ? ? Pr1(S1);
И для завершения рассмотрения вариантов операций соединения, рассмотрим пример, иллюстрирующий работу операции полного внешнего соединения. Введем два отношения r1(S1) и r2(S2) и условие соединения.
Пусть
r1(S1)
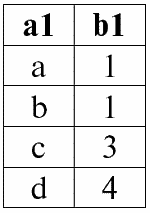
r2(S2):
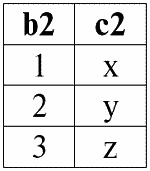
И пусть условием соединения отношений r1(S1) и r2(S2) будет: P = (b1 = b2), как и в предыдущих примерах.
Тогда результатом операции полного внешнего соединения отношений r1(S1) и r2(S2) по условию P = (b1 = b2) будет следующая таблица:
r1(S1) ?? Pr2(S2):
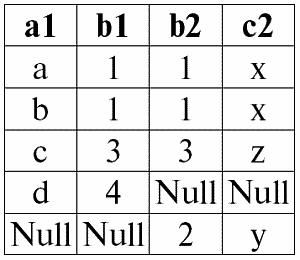
Итак, мы видим, что операция полного внешнего соединения наглядно оправдала свое определение как объединения результатов операций левого и правого внешних соединений. Результирующее отношение операции внутреннего соединения дополнено одновременно несоединимыми кортежами как левого (первого, r1(S1)), так и правого (второго, r2(S2)) исходного отношения-операнда.
- 15.2. Настройка соединения ADSL
- 7.12. Асинхронное выполнение задач с помощью операций
- 8.3. Настройка DSL-соединения в Ubuntu
- Реентерабельные соединения
- Директивы, атрибуты и коды операций CIL
- Глава 3. Варианты установки
- 7.11. Синхронное выполнение задач с помощью операций
- Старшинство операций
- 2.2.3. Настройка ADSL-соединения
- Глава 11. Соединения точка-точка и ретрансляторы
- 6.2. Типичные ошибки при проведении программ продвижения и варианты их устранения
- 4. Свойства унарных операций




