Книга: Учебное пособие по курсу «Нейроинформатика»

Примеры сетей и алгоритмов их обучения

В этом разделе намеренно допущено отступление от общей методики — не смешивать разные компоненты. Это сделано для облегчения демонстрации построения нейронных сетей обратного распространения, позволяющих реализовать на них большинство известных алгоритмов обучения нейронных сетей.

Сети Хопфилда

Классическая сеть Хопфилда [312], функционирующая в дискретном времени, строится следующим образом. Пусть {eⁱ} — набор эталонных образов (i=1, …, m). Каждый образ, включая и эталоны, имеет вид n-мерного вектора с координатами, равными нулю или единице. При предъявлении на вход сети образа x сеть вычисляет образ, наиболее похожий на x. В качестве меры близости образов выберем скалярное произведение соответствующих векторов. Вычисления проводятся по следующей формуле:

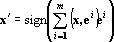
Эта процедура выполняется до тех пор, пока после очередной итерации не окажется, что x=x'. Вектор x, полученный в ходе последней итерации, считается ответом. Для нейросетевой реализации формула работы сети переписывается в следующем виде:

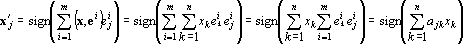
или

x'=sign(Ax),

где

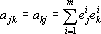
На рис. 17 приведена схема сети Хопфилда [312] для распознавания четырехмерных образов. Обычно сети Хопфилда [312] относят к сетям с формируемой синаптической картой. Однако, используя разработанный в первой части главы набор элементов, можно построить обучаемую сеть. Для построения такой сети используем «прозрачные» пороговые элементы. Ниже приведен алгоритм обучения сети Хопфилда [312].

1. Положим все синаптические веса равными нулю.

2. Предъявим сети первый эталон e? и проведем один такт функционирования вперед, то есть цикл будет работать не до равновесия, а один раз (см. рис. 17б).

3. Подадим на выход каждого нейрона соответствующую координату вектора e? (см. рис. 17в). Поправка, вычисленная на j-ом синапсе i-го нейрона, равна произведению сигнала прямого функционирования на сигнал обратного функционирования. Поскольку при обратном функционировании пороговый элемент прозрачен, а сумматор переходит в точку ветвления, то поправка равна e_i?e_j?.

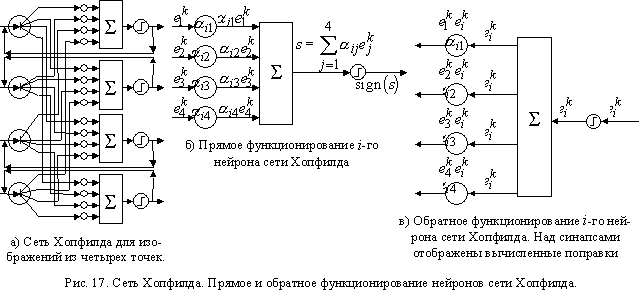
4. Далее проведем шаг обучения с параметрами обучения, равными единице. В результате получим ?_ij=e_i?e_j?.

Повторяя этот алгоритм, начиная со второго шага, для всех эталонов получим

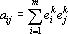
Сеть Кохонена

Сети Кохонена [131, 132] (частный случай метода динамических ядер [224, 262]) являются типичным представителем сетей решающих задачу классификации без учителя. Рассмотрим пространственный вариант сети Кохонена. Дан набор из m точек {xp} в n-мерном пространстве. Необходимо разбить множество точек {xp} на k классов близких в смысле квадрата евклидова расстояния. Для этого необходимо найти k точек ?^l таких, что

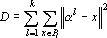
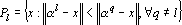
Существует множество различных алгоритмов решения этой задачи. Рассмотрим наиболее эффективный из них.

1. Зададимся некоторым набором начальных точек ?^l.

2. Разобьем множество точек {xp} на k классов по правилу

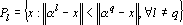
3. По полученному разбиению вычислим новые точки ?^l из условия минимальности

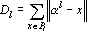
Обозначив через |P_i| число точек в i-ом классе, решение задачи, поставленной на третьем шаге алгоритма, можно записать в виде

Второй и третий шаги алгоритма будем повторять до тех пор, пока набор точек ?^l не перестанет изменяться. После окончания обучения получаем нейронную сеть, способную для произвольной точки x вычислить квадраты евклидовых расстояний от этой точки до всех точек ?^l и, тем самым, отнести ее к одному из k классов. Ответом является номер нейрона, выдавшего минимальный сигнал.

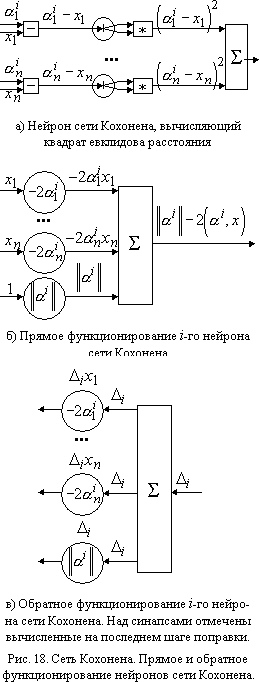
Теперь рассмотрим сетевую реализацию. Во первых, вычисление квадрата евклидова расстояния достаточно сложно реализовать в виде сети (рис. 18а). Однако заметим, что нет необходимости вычислять квадрат расстояния полностью. Действительно,

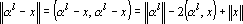
Отметим, что в последней формуле первое слагаемое не зависит от точки x, второе вычисляется адаптивным сумматором, а третье одинаково для всех сравниваемых величин. Таким образом, легко получить нейронную сеть, которая вычислит для каждого класса только первые два слагаемых (рис. 18б).

Второе соображение, позволяющее упростить обучение сети, состоит в отказе от разделения второго и третьего шагов алгоритма.

Алгоритм классификации.

1. На вход нейронной сети, состоящей из одного слоя нейронов, приведенных на рис. 18б, подается вектор x.

2. Номер нейрона, выдавшего минимальный ответ, является номером класса, к которому принадлежит вектор x.

Алгоритм обучения.

1. Полагаем поправки всех синапсов равными нулю.

2. Для каждой точки множества {xp} выполняем следующую процедуру.

 1. Предъявляем точку сети для классификации.

 2. Пусть при классификации получен ответ — класс l. Тогда для обратного функционирования сети подается вектор ?, координаты которого определяются по следующему правилу:

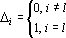
 3. Вычисленные для данной точки поправки добавляются к ранее вычисленным.

3. Для каждого нейрона производим следующую процедуру.

 1. Если поправка, вычисленная последним синапсом равна 0, то нейрон удаляется из сети.

 2. Полагаем параметр обучения равным величине, обратной к поправке, вычисленной последним синапсом.

 3. Вычисляем сумму квадратов накопленных в первых n синапсах поправок и, разделив на –2, заносим в поправку последнего синапса.

 4. Проводим шаг обучения с параметрами h₁=0, h₂=-2.

4. Если вновь вычисленные синаптические веса отличаются от полученных на предыдущем шаге, то переходим к первому шагу алгоритма.

В пояснении нуждается только второй и третий шаги алгоритма. Из рис. 18в видно, что вычисленные на шаге 2.2 алгоритма поправки будут равны нулю для всех нейронов, кроме нейрона, выдавшего минимальный сигнал. У нейрона, выдавшего минимальный сигнал, первые n поправок будут равны координатам распознававшейся точки x, а поправка последнего синапса равна единице. После завершения второго шага алгоритма поправка последнего синапса i-го нейрона будет равна числу точек, отнесенных к i-му классу, а поправки остальных синапсов этого нейрона равны сумме соответствующих координат всех точек i — о класса. Для получения правильных весов остается только разделить все поправки первых n синапсов на поправку последнего синапса, положить последний синапс равным сумме квадратов полученных величин, а остальные синапсы — полученным для них поправкам, умноженным на –2. Именно это и происходит при выполнении третьего шага алгоритма.

Персептрон Розенблатта

Персептрон Розенблатта [146, 181] является исторически первой обучаемой нейронной сетью. Существует несколько версий персептрона. Рассмотрим классический персептрон — сеть с пороговыми нейронами и входными сигналами, равными нулю или единице. Опираясь на результаты, изложенные в работе [146] можно ввести следующие ограничения на структуру сети.

1. Все синаптические веса могут быть целыми числами.

2. Многослойный персептрон по своим возможностям эквивалентен двухслойному. Все нейроны имеют синапс, на который подается постоянный единичный сигнал. Вес этого синапса далее будем называть порогом. Каждый нейрон первого слоя имеет единичные синаптические веса на всех связях, ведущих от входных сигналов, и его порог равен числу входных сигналов сумматора, уменьшенному на два и взятому со знаком минус.

Таким образом, можно ограничиться рассмотрением только двухслойных персептронов с не обучаемым первым слоем. Заметим, что для построения полного первого слоя пришлось бы использовать 2nнейронов, где n — число входных сигналов персептрона. На рис. 19а приведена схема полного персептрона для трехмерного вектора входных сигналов. Поскольку построение такой сети при достаточно большом n невозможно, то обычно используют некоторое подмножество нейронов первого слоя. К сожалению, только полностью решив задачу можно точно указать необходимое подмножество. Обычно используемое подмножество выбирается исследователем из каких-то содержательных соображений или случайно.

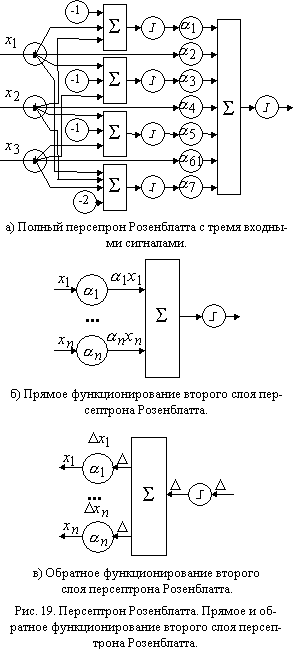
Классический алгоритм обучения персептрона является частным случаем правила Хебба. Поскольку веса связей первого слоя персептрона являются не обучаемыми, веса нейрона второго слоя в дальнейшем будем называть просто весами. Будем считать, что при предъявлении примера первого класса персептрон должен выдать на выходе нулевой сигнал, а при предъявлении примера второго класса — единичный. Ниже приведено описание алгоритма обучения персептрона.

1. Полагаем все веса равными нулю.

2. Проводим цикл предъявления примеров. Для каждого примера выполняется следующая процедура.

 1. Если сеть выдала правильный ответ, то переходим к шагу 2.4.

 2. Если на выходе персептрона ожидалась единица, а был получен ноль, то веса связей, по которым прошел единичный сигнал, уменьшаем на единицу.

 3. Если на выходе персептрона ожидался ноль, а была получена единица, то веса связей, по которым прошел единичный сигнал, увеличиваем на единицу.

 4. Переходим к следующему примеру. Если достигнут конец обучающего множества, то переходим к шагу 3, иначе возвращаемся на шаг 2.1.

3. Если в ходе выполнения второго шага алгоритма хоть один раз выполнялся шаг 2.2 или 2.3 и не произошло зацикливания, то переходим к шагу 2. В противном случае обучение завершено.

В этом алгоритме не предусмотрен механизм отслеживания зацикливания обучения. Этот механизм можно реализовывать по разному. Наиболее экономный в смысле использования дополнительной памяти имеет следующий вид.

1. k=1; m=0. Запоминаем веса связей.

2. После цикла предъявлений образов сравниваем веса связей с запомненными. Если текущие веса совпали с запомненными, то произошло зацикливание. В противном случае переходим к шагу 3.

3. m=m+1. Если m<k, то переходим ко второму шагу.

4. k=2k;m=0. Запоминаем веса связей и переходим к шагу 2.

Поскольку длина цикла конечна, то при достаточно большом k зацикливание будет обнаружено.

Для использования в обучении сети обратного функционирования, необходимо переписать второй шаг алгоритма обучения в следующем виде.

2. Проводим цикл предъявления примеров. Для каждого примера выполняется следующая процедура.

2.1. Если сеть выдала правильный ответ, то переходим к шагу 2.5.

2.2. Если на выходе персептрона ожидалась единица, а был получен ноль, то на выход сети при обратном функционировании подаем ?=-1.

2.3. Если на выходе персептрона ожидался ноль, а была получена единица, то на выход сети при обратном функционировании подаем ?=1.

2.4. Проводим шаг обучения с единичными параметрами.

2.5. Переходим к следующему примеру. Если достигнут конец обучающего множества, то переходим к шагу 3, иначе возвращаемся на шаг 2.1.

На рис. 19в приведена схема обратного функционирования нейрона второго слоя персептрона. Учитывая, что величины входных сигналов этого нейрона равны нулю или единице, получаем эквивалентность модифицированного алгоритма исходному. Отметим также, что при обучении персептрона впервые встретились не обучаемые параметры — веса связей первого слоя.

Оглавление книги