Книга: Программирование на языке Пролог для искусственного интеллекта

14.3. Правила типа "если-то" для представления знаний

14.3. Правила типа "если-то" для представления знаний

В качестве кандидата на использование в экспертной системе можно рассматривать, в принципе, любой непротиворечивый формализм, в рамках которого можно описывать знания о некоторой проблемной области. Однако самым популярным формальным языком представления знаний является язык правил типа "если-то" (или кратко: "если-то"-правил), называемых также продукциями. Каждое такое правило есть, вообще говоря, некоторое условное утверждение, но возможны и различные другие интерпретации. Вот примеры:

• если предварительное условие P то заключение (вывод) С

• если ситуация S то действие А

• если выполнены условия C1 и C2 то не выполнено условие С

"Если-то"-правила обычно оказываются весьма естественным выразительным средством представления знаний. Кроме того, они обладают следующими привлекательными свойствами:

• Модульность: каждое правило описывает небольшой, относительно независимый фрагмент знаний.

• Возможность инкрементного наращивания: добавление новых правил в базу знаний происходит относительно независимо от других правил.

• Удобство модификации (как следствие модульности): старые правила можно изменять и заменять на новые относительно независимо от других правил.

• Применение правил способствует прозрачности системы.

Последнее свойство — это важное, отличительное свойство экспертных систем. Под прозрачностью мы понимаем способность системы к объяснению принятых решений и полученных результатов. Применение "если-то"-правил облегчает получение ответов на следующие основные типы вопросов пользователя:

(1) Вопросы типа "как": Как вы пришли к этому выводу?

(2) Вопросы типа "почему": Почему вас интересует эта информация?

Механизмы, основанные на "если-то"-правилах, для формирования ответов на подобные вопросы мы обсудим позже.

если

 1 тип инфекции — это первичная бактериемия и

 2 материал для посева был отобран стерильно, и

 3 предполагаемые ворота инфекции — желудочно-кишечный тракт

то

 имеются веские аргументы (0.7) за то,

 что инфекционный агент является бактерией

Рис. 14.2. "Если-то"-правило медицинской консультативной системы MYCIN (Shortliffe, 1976). Параметр 0.7 показывает степень доверия этому правилу.

"Если-то"-правила часто применяют для определения логических отношений между понятиями предметной области. Про чисто логические отношения можно сказать, что они принадлежат к "категорическим знаниям", "категорическим" — потому, что соответствующие утверждения всегда, абсолютно верны. Однако в некоторых предметных областях, таких, как медицинская диагностика, преобладают "мягкие" или вероятностные знания. Эти знания являются "мягкими"; в том смысле, что говорить об их применимости к любым практическим ситуациям можно только до некоторой степени ("часто, но не всегда"). В таких случаях используют модифицированные "если-то"-правила, дополняя их логическую интерпретацию вероятностной оценкой. Например:

если условие А то заключение В с уверенностью F

Рис. 14.2, 14.3 и 14.4 дают представление о разнообразии способов, которыми знания могут быть выражены при помощи "если-то"-правил. На этих рисунках приведены примеры правил из трех различных систем, основанных на знаниях: медицинской консультативной системы MYCIN, системы AL/X для диагностики неисправностей в оборудовании и системы AL3 для решения шахматных задач.

Вообще говоря, если вы хотите разработать серьезную экспертную систему для некоторой выбранной вами предметной области, вы должны провести консультации с экспертами в этой области и многое узнать о ней сами. Достигнуть определенного понимания предметной области после общения с экспертами и чтения литературы, а затем облечь это понимание в форму представления знаний в рамках выбранного формального языка — это искусство, называемое инженерией знаний. Как правило, это сложная задача, требующая больших усилий, чего мы не можем себе позволить в данной книге. Но какая-нибудь предметная область и какая-нибудь база данных нам необходимы в качестве материала для экспериментов. С практической точки зрения нам для этой цели вполне подойдет "игрушечная" база знаний. На рис. 14.5 показана часть такой базы знаний. Она состоит из простых правил, помогающих идентифицировать животных по их основным признаками в предположении, что задача идентификации ограничена только небольшим числом разных животных.

если

 давление в v-01 достигло уровня открытия выпускного клапана

то

 выпускной клапан в v-01 открылся

 [N=0.005, S=400]

если

 давление в v-01 не достигло уровня открытия выпускного клапана и выпускной клапан в v-01 открылся

то

 преждевременное открытие выпускного клапана (сместилась установка порогового давления)

 [N=0.001, S=2000]

Рис. 14.3. Два правила из демонстрационной базы знаний системы AL/X для диагностики неисправностей (Reiter 1980). N и S — величины "необходимости" и "достаточности", детально описанные в разд. 14.7. Величина S указывает степень, с которой условие влечет за собой заключение (вывод). Величина N указывает, до какой степени истинность условия необходима для того, чтобы заключение было истинным.

если

 1 существует гипотеза H, что план P ведет к успеху, и

 2 существуют две гипотезы

  H1, что план P1 опровергает план P, и

  Н2, что план Р2 опровергает план P, и

 3 имеют место факты:

   гипотеза H1 ложна и

   гипотеза Н2 ложна

то

 1 породить гипотезу Н3, что составной план "P1 или Р2" опровергает план P, и

 2 породить факт: из  Н3 следует не( H)

Рис. 14.4. Правило уточнения плана из системы AL3 для решения шахматных задач (Bratko 1982).

Правила, содержащиеся в базе знаний, имеют вид

ИмяПравила : если Условие то Заключение

где Заключение — это простое утверждение, а Условие — это набор простых утверждений, соединенных между собой операторами и и или. Мы также разрешим в части условия использовать оператор не, хотя и с некоторыми оговорками. При надлежащем прологовском определении этих операторов (как это сделано на рис. 14.5) правила станут синтаксически верными предложениями Пролога. Заметим, что оператор и связывает операнды сильнее, чем или, что соответствует обычным соглашениям.

% Небольшая база знаний для идентификации животных
:- op( 100, xfx, [имеет, 'кормит детенышей',
 'не может', ест, откладывает, это]).
:- op( 100, xf, [плавает, летает, хорошо]).
прав1: если
 Животное имеет шерсть
 или
 Животное 'кормит детенышей' молоком
то
 Животное это млекопитающее.
прав2: если
 Животное имеет перья
 или
 Животное летает и
 Животное откладывает яйца
то
 Животное это птица.
прав3: если
 Животное это млекопитающее и
 ( Животное ест мясо
   или
   Животное имеет 'острые зубы' и
   Животное имеет когти и
   Животное имеет
   'глаза, направленные вперед' )
то
 Животное это хищник.
прав4: если
 Животное это хищник и
 Животное имеет
  'рыжевато-коричневый цвет' и
 Животное имеет 'темные пятна'
то
 Животное это гепард.
прав5: если
 Животное это хищник и
 Животное имеет
  'рыжевато-коричневый цвет' и
 Животное имеет 'черные полосы'
то
 Животное это тигр.
прав6: если
 Животное это птица и
 Животное 'не может' летать и
 Животное плавает
то
 Животное это пингвин.
прав7: если
 Животное это птица и
 Животное летает хорошо
то
 Животное это альбатрос.
факт: X это животное :-
 принадлежит( X, [гепард, тигр, пингвин, альбатрос]).
можно_спросить( _ 'кормит детенышей' _,
 'Животное' 'кормит детенышей' 'Чем').
можно_спросить( _ летает, 'Животное' летает).
можно_спросить( _ откладывает яйца,
 'Животное' откладывает яйца).
можно_спросить( _ ест _, 'Животное' ест 'Что').
можно_спросить( _ имеет _,'Животное' имеет 'Нечто').
можно_спросить( _ 'не может' _,
 'Животное' 'не может' 'Что делать').
можно_спросить( _ плавает, 'Животное' плавает).
можно_спросить( _ летает хорошо,
 'Животное' летает хорошо).

Рис. 14.5. Простая база знаний для идентификации животных. Заимствовано из Winston (1984). Отношение "можно_спросить" определяет вопросы, которые можно задавать пользователю. Операторы если, то, и, или определены на рис. 14.10.

Рассмотрим еще одну небольшую базу знаний, которая может помочь локализовать неисправности в простой электрической схеме, состоящей из электрических приборов и предохранителей. Электрическая схема показана на рис. 14.6. Вот одно из возможных правил:

если

 лампа1 включена и

 лампа1 не работает  и

 предохранитель1 заведомо цел

то

 лампа1 заведомо неисправна.

Вот другой пример правила:

если

 радиатор работает

то

 предохранитель1 заведомо цел.

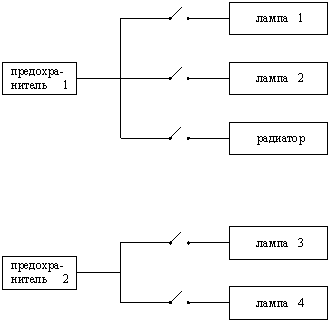
Рис. 14.6. Соединения между предохранителями и приборами в простой электрической схеме.

Эти два правила опираются на некоторые факты (относящиеся к нашей конкретной схеме), а именно что лампа1 соединена с предохранитель1 и что лампа1 и радиатор имеют общий предохранитель. Для другой схемы нам понадобится еще один набор правил. Поэтому было бы лучше сформулировать правила в более общем виде (используя прологовские переменные) так, чтобы они были применимы к любой схеме, а затем уже дополнять их информацией о конкретной схеме. Например, вот одно из полезных правил: если прибор включен, но не работает, а соответствующий предохранитель цел, то прибор неисправен. На наш формальный язык это транслируется так:

правило_поломки:
 если
  Прибор включен и
  не (Прибор работает) и
  Прибор соединен с Предохранитель и
  Предохранитель заведомо цел
 то
  Прибор заведомо неисправен.

База знаний такого рода показана на рис. 14. 7.

% Небольшая база знаний для локализации неисправностей в
% электрической схеме
% Если прибор включен, но не работает, и предохранитель цел,
% то прибор неисправен.
правило_поломки:
 если
  вкл( Прибор) и
  прибор( Прибор) и
  не работает( Прибор) и
  соед( Прибор, Предохр) и
  доказано( цел( Предохр) )
 то
  доказано( неиспр( Прибор) ).
% Если устройство работает, то его предохранитель цел
правило_цел_предохр:
 если
  соед( Прибор, Предохр)
  и работает( Прибор)
 то
  доказано( цел( Предохр) ).
% Если два различных прибора подключены к одному и тому же
% предохранителю, оба включены и не работают, то предохранитель
% сгорел.
% ЗАМЕЧАНИЕ: предполагается, что из двух приборов неисправных -
% не более одного!
правило_предохр:
 если
  соед( Прибор1, Предохр) и
  вкл( Прибор1) и
  не работает( Прибор1) и
  общ_предохр( Прибор2, Прибор1) и
  вкл( Прибор2) и
  не работает( Прибор2)
 то
  доказано( сгорел( Предохр) ).
правило_общ_предохр:
 если
  соед( Прибор1, Предохр) и
  соед( Прибор2, Предохр) и
  различны( Прибор1, Прибор2)
 то
  общ_предохр( Прибор1, Прибор2).
факт: различны( X, Y) :- not (X=Y).
факт: прибор( радиатор).
факт: прибор( лампа1).
факт: прибор( лампа2).
факт: прибор( лампа3).
факт: прибор( лампа4).
факт: соед( лампа1, предохр1).
факт: соед( лампа2, предохр1).
факт: соед( радиатор, предохр1).
факт: соед( лампа3, предохр2).
факт: соед( лампа4, предохр2).
можно_спросить( вкл( П), вкл( 'Прибор') ).
можно_спросить( работает( П), работает(' Прибор')).

Рис. 14.7. База знаний для локализации неисправностей в схеме, показанной на рис. 14.6.

14.1. Рассмотрите "если-то"-правила рис. 14.2-14.4 и транслируйте их в нашу систему обозначений для правил. Предложите расширение нотации, чтобы, при необходимости, можно было работать с оценками уверенности.

14.2. Придумайте какую-нибудь задачу принятия решений и сформулируйте соответствующие знания в форме "если-то"-правил. Можете рассмотреть, например, планирование отпуска, предсказание погоды, простой медицинский диагноз и лечение и т.п.

Оглавление книги