Книга: Программирование на языке Пролог для искусственного интеллекта

11.3.2. Древовидное представление множества кандидатов

11.3.2. Древовидное представление множества кандидатов

Рассмотрим теперь еще одно изменение нашей программы поиска в ширину. До сих пор мы представляли множества путей-кандидатов как списки путей. Это расточительный способ, поскольку начальные участки путей являются общими для нескольких из них. Таким образом, эти общие части путей приходится хранить во многих экземплярах. Избежать избыточности помогло бы более компактное представление множества кандидатов. Таким более компактным представлением является дерево, в котором общие участки путей хранятся в его верхней части без дублирования. Будем использовать в программе следующее представление дерева. Имеется два случая:

Случай 1: Дерево состоит только из одной вершины В; В этом случае оно имеет вид терма л( В); Функтор л указывает на то, что В — это лист дерева.

Случай 2: Дерево состоит из корневой вершины В и множества поддеревьев Д1, Д2, …. Такое дерево представляется термом

д( В, Пд)

где Пд — список поддеревьев:

Пд = [ Д1, Д2, ...]

В качестве примера рассмотрим ситуацию, которая возникает после того, как порождены три уровня дерева рис. 11.9. Множество путей-кандидатов в случае спискового представления имеет вид:

[ [d, b, a], [e, b, а], [f, c, a], [g, c, a] ]

В виде дерева это множество выглядит так:

д( а, [д( b, [л( d), л( e)] ), д( с, [л( f), л( g)] )] )

На первый взгляд древовидное представление кажется еще более расточительным, чем списковое, однако это всего лишь поверхностное впечатление, связанное с компактностью прологовской нотации для списков.

В случае спискового представления множества кандидатов эффект распространения процесса в ширину достигался за счет перемещения продолженных путей в конец списка. В нашем случае мы уже не можем использовать этот прием, поэтому программа несколько усложняется. Ключевую роль в нашей программе будет играть отношение

расширить( Путь, Дер, Дер1, ЕстьРеш, Решение)

На рис. 11.12 показано, как связаны между собой аргументы отношения расширить. При каждом обращении к расширить переменные Путь и Дер будут уже конкретизированы. Дер — поддерево всего дерева поиска, одновременно оно служит для представления множества путей-кандидатов внутри этого поддерева. Путь — это путь, ведущий из стартовой вершины в корень поддерева Дер. Самая общая идея алгоритма — получить поддерево Дер1 как результат расширения Дер на один уровень. Но в случае, когда в процессе расширения поддерева Дер встретится целевая вершина, процедура расширить должна сформировать соответствующий решающий путь.

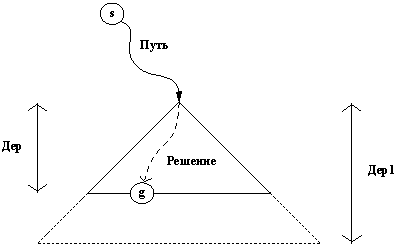
Рис. 11.12. Отношение paсширить( Путь, Дер, Дер1, ЕстьРеш, Решение):  s — стартовая вершина, g — целевая вершина. Решение — это Путь, продолженный вплоть до g. Дер1 — результат расширения дерева Дер на один уровень вниз.

Итак, процедура расширить будет порождать два типа результатов. На конкретный вид результата будет указывать значение переменной ЕстьРеш:

(1) ЕстьРеш = да

Решение = решающий путь, т.е. Путь, продолженный до целевой вершины.

Дер1 = неконкретизировано.

Разумеется, такой тип результата получится только в том случае, когда Дер будет содержать целевую вершину. Добавим также, что эта целевая вершина обязана быть листом поддерева Дер.

(2) ЕстьРеш = нет

Дер1 = результат расширения поддерева Дер на один уровень вниз от своего "подножья". Дер1 не содержит ни одной "тупиковой" ветви из Дер, т.е. такой ветви, что она либо не может быть продолжена из-за отсутствия преемников, либо любое ее продолжение приводит к циклу.

Решение = неконкретизировано.

Если в дереве Дер нет ни одной целевой вершины и, кроме того, оно не может быть расширено, то процедура расширить терпит неудачу.

Процедура верхнего уровня для поиска в ширину

вширину( Дер, Решение)

отыскивает Решение либо среди множества кандидатов Дер, либо в его расширении. На рис. 11.3 показано, как выглядит программа целиком. В этой программе имеется вспомогательная процедура расширитьвсе. Она расширяет все деревья из некоторого списка, и затем, выбросив все "тупиковые" деревья", собирает все полученные расширенные деревья в один новый список. Используя механизм возвратов, она также порождает все решения, обнаруженные в деревьях из списка. Имеется одна дополнительная деталь: по крайней мере одно из деревьев должно "вырасти". Если это не так, то процедуре расширитьвсе не удается получить ни одного расширенного дерева - все деревья из списка оказываются "тупиковыми".

% ПОИСК В ШИРИНУ
% Множество кандидатов представлено деревом
решить( Старт, Решение) :-
 вширину( л( Старт), Решение).
вширину( Дер, Решение) :-
 расширить( [], Дер, Дер1, ЕстьРеш, Решение),
 ( ЕстьРеш = да;
   ЕстьРеш = нет, вширину( Дер1, Решение) ).
расширить( П, Л( В), _, да, [В | П] ) :-
 цель( В).
расширить( П, Л( В), д( В, Пд), нет, _ ) :-
 bagof( л( B1),
 ( после( В, B1), not принадлежит( В1, П)), Пд).
расширить( П, д( В, Пд), д( В, Пд1), ЕстьРеш, Реш) :-
 расширитьвсе( [В | П], Пд, [ ], Пд1, ЕстьРеш, Реш).
расширитьвсе( _, [ ], [Д | ДД], [Д | ДД], нет, _ ).
  % По крайней мере одно дерево должно вырасти
расширитьвсе( П, [Д | ДД], ДД1, Пд1, ЕстьРеш, Реш) :-
 расширить ( П, Д, Д1, ЕстьРеш1, Реш),
 ( ЕстьРеш 1= да, ЕстьРеш = да;
   ЕстьРеш1 = нет, !,
   расширитьвсе( П, ДД, [Д1 | ДД1], Пд1, ЕстьРеш, Реш));
 расширитьвсе( П, ДД, ДД1, Пд1, ЕстьРеш, Реш ).

Рис. 11.13. Реализация поиска в ширину с использованием древовидного представления множества путей-кандидатов.

Мы разработали эту более сложную реализацию поиска в ширину не только для того, чтобы получать программу более экономичную по сравнению с предыдущей версией, но также и потому, что такое решение задачи может послужить хорошим стартом для перехода к усложненным программам поиска, управляемым эвристиками, таким как программа поиска с предпочтением из гл. 12.

11.5. Перепишите программу поиска в ширину рис. 11.10, используя разностное представление для списка путей-кандидатов и покажите, что в результате получится программа, приведенная на рис. 11.11. Зачем в программу рис. 11.11 включена цель

Пути == Z

Проверьте, что случится при поиске в пространстве состояний рис. 11.9, если эту цель опустить. Различие в выполнении программы, возникнет только при попытке найти новые решения в ситуации, когда не осталось больше ни одного решения.

11.6. Как программы настоящего раздела можно использовать для поиска, начинающегося от стартового множества вершин, вместо одной стартовой вершины?

11.7. Как программы этой главы можно использовать для поиска в обратном направлении, т.е. от целевой вершины к стартовой вершине (или к одной из стартовых вершин, если их несколько). Указание: переопределите отношение после. В каких ситуациях обратный поиск будет иметь преимущества перед прямым поиском?

11.8. Иногда выгодно сделать поиск двунаправленным, т.е. продвигаться одновременно с двух сторон от стартовой и целевой вершин. Поиск заканчивается, когда оба пути "встречаются". Определите пространство поиска (отношение после) и целевое отношение для заданного графа таким образом, чтобы наши процедуры поиска в действительности выполняли двунаправленный поиск.

11.9. Проведите эксперименты с различными методами поиска применительно к задаче планирования в "мире кубиков".

Оглавление книги