Книга: Программирование на языке Пролог для искусственного интеллекта

9.5.1. Представление графов

9.5.1. Представление графов

Графы используются во многих приложениях, например для представления отношений, ситуаций или структур задач. Граф определяется как множество вершин вместе с множеством ребер, причем каждое ребро задается парой вершин. Если ребра направлены, то их также называют дугами. Дуги задаются упорядоченными парами. Такие графы называются направленными. Ребрам можно приписывать стоимости, имена или метки произвольного вида, в зависимости от конкретного приложения. На рис. 9.18 показаны примеры графов.

В Прологе графы можно представлять различными способами. Один из них — каждое ребро записывать в виде отдельного предложения. Например, графы, показанные на рис. 9.18, можно представить в виде следующего множества предложений:

связь( а, b).
связь( b, с).
...
дуга( s, t, 3).
дуга( t, v, 1).
дуга( u, t, 2).
...

Другой способ — весь граф представлять как один объект. В этом случае графу соответствует пара множеств — множество вершин и множество ребер. Каждое множество можно задавать при помощи списка, каждое ребро — парой вершин. Для объединения двух множеств в пару будем применять функтор граф, а для записи ребра — функтор p. Тогда (ненаправленный) граф рис. 9.18 примет вид:

G1 = граф( [a, b, c, d],
 [p( а, b), p( b, d), p( b, с), p( c, d)] )

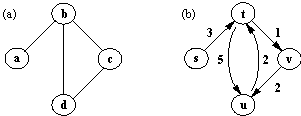
Рис. 9.18. (а) Граф. (b) Направленный граф. Каждой дуге приписана ее стоимость.

Для представления направленного графа (рис. 9.18), применив функторы диграф и д (для дуг), получим

G2 = диграф( [s, t, u, v],
 [д( s, t, 3), д( t, v, 1), д( t, u, 5), д( u, t, 2),
  д( v, u, 2) ] )

Если каждая вершина графа соединена ребром еще по крайней мере с одной вершиной, то в представлении графа можно опустить множество вершин, поскольку оно неявным образом содержится в списке ребер.

Еще один способ представления графа — связать с каждой вершиной список смежных с ней вершин. В этом случае граф превращается в список пар, каждая из которых состоит из вершины- плюс ее список смежности. Наши графы (рис. 9.18), например, можно представить как

G1 = [ a->[b1, b->[a, c, d], c->[b, d], d->[b, c] ]
G2 = [s->[t/3], t->[u/5, v/l], u->[t/2], v->[u/2]]

Здесь символы '->' и '/' — инфиксные операторы.

Какой из способов представления окажется более удобным, зависит от конкретного приложения, а также от того, какие операции имеется в виду выполнять над графами. Вот типичные операции:

• найти путь между двумя заданными вершинами;

• найти подграф, обладающий некоторыми заданными свойствами.

Примером последней операции может служить построение основного дерева графа. В последующих разделах, мы рассмотрим некоторые простые программы для поиска пути в графе и построения основного дерева. 

Оглавление книги