Книга: Distributed operating systems
6.3.2. Sequential Consistency
6.3.2. Sequential Consistency
While strict consistency is the ideal programming model, it is nearly impossible to implement in a distributed system. Furthermore, experience shows that programmers can often manage quite well with weaker models. For example, all textbooks on operating systems discuss critical sections and the mutual exclusion problem. This discussion always includes the caveat that properly-written parallel programs (such as the producer-consumer problem) should not make any assumptions about the relative speeds of the processes or how their statements will interleave in time. Counting on two events within one process to happen so quickly that the other process will not be able to do something in between is looking for trouble. Instead, the reader is taught to program in such a way that the exact order of statement execution (in fact, memory references) does not matter. When the order of events is essential, semaphores or other synchronization operations should be used. Accepting this argument in fact means learning to live with a weaker memory model. With some practice, most parallel programmers are able to adapt to it.
Sequential consistency is a slightly weaker memory model than strict consistency. It was first defined by Lamport (1979), who said that a sequentially consistent memory is one that satisfies the following condition:
The result of any execution is the same as if the operations of all processors were executed in some sequential order, and the operations of each individual processor appear in this sequence in the order specified by its program.
What this definition means is that when processes run in parallel on different machines (or even in pseudoparallel on a timesharing system), any valid interleaving is acceptable behavior, but all processes must see the same sequence of memory references. A memory in which one process (or processor) sees one interleaving and another process sees a different one is not a sequentially consistent memory. Note that nothing is said about time; that is, there is no reference to the "most recent" store. Note that in this context, a process "sees" writes from all processes but only its own reads.
That time does not play a role can be seen from Fig. 6-13. A memory behaving as shown in Fig. 6-13(a) is sequentially consistent even though the first read done by P2 returns the initial value of 0 instead of the new value of 1.

Fig. 6-13. Two possible results of running the same program.
Sequentially consistent memory does not guarantee that a read returns the value written by another process a nanosecond earlier, or a microsecond earlier, or even a minute earlier. It merely guarantees that all processes see all memory references in the same order. If the program that generated Fig. 6-13(a) is run again, it might give the result of Fig. 6-13(b). The results are not deterministic. Running a program again may not give the same result in the absence of explicit synchronization operations.
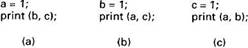
Fig. 6-14. Three parallel processes.
To make this point more explicit, let us consider the example of Fig. 6-14 (Dubois et al., 1988). Here we see the code for three processes that run in parallel on three different processors. All three processes share the same sequentially consistent distributed shared memory, and all have access to the variables a, b, and c. From a memory reference point of view, an assignment should be seen as a write, and a print statement should be seen as a simultaneous read of its two parameters. All statements are assumed to be atomic.
Various interleaved execution sequences are possible. With six independent statements, there are potentially 720 (6!) possible execution sequences, although some of these violate program order. Consider the 120 (5!) sequences that begin with a=1. Half of these have print(a, c) before b=1 and thus violate program order. Half also have print(a, b) before c=1 and also violate program order. Only ? of the 120 sequences or 30 are valid. Another 30 valid sequences are possible starting with b=1 and another 30 can begin with c=1, for a total of 90 valid execution sequences. Four of these are shown in Fig. 6-15.
| a = 1; | a = 1; | b = 1; | b = 1; |
| print(b, c); | b = 1; | c= 1; | a= 1; |
| b = 1; | print(a, c); | print(a, b); | c = 1; |
| print(a, c); | print(b, c); | print(a, c); | print(a, c); |
| c = 1; | c = 1; | a = 1; | print(b, c); |
| print(a, c); | print(a, b); | print(b, c); | print(a, b); |
| Prints: 001011 | Prints: 101011 | Prints: 010111 | Prints: 111111 |
| Signature: 001011 | Signature: 101011 | Signature: 110101 | Signature: 111111 |
| (a) | (b) | (c) | (d) |
Fig. 6-15. Four valid execution sequences for the program of Fig. 6-14. The vertical axis is time, increasing downward.
In Fig. 6-15(a), the three processes are run in order, first P1, then P2, then P3. The other three examples demonstrate different, but equally valid, inter-leavings of the statements in time. Each of the three processes prints two variables. Since the only values each variable can take on are the initial value (0), or the assigned value (1), each process produces a 2-bit string. The numbers after Prints are the actual outputs that appear on the output device.
If we concatenate the output of P1, P2, and P3 in that order, we get a 6-bit string that characterizes a particular interleaving of statements (and thus memory references). This is the string listed as the Signature in Fig. 6-15. Below we will characterize each ordering by its signature rather than by its printout.
Not all 64 signature patterns are allowed. As a trivial example, 000000 is not permitted, because that would imply that the print statements ran before the assignment statements, violating Lamport's requirement that statements are executed in program order. A more subtle example is 001001. The first two bits, 00, mean that b and c were both 0 when P1 did its printing. This situation occurs only when P1 executes both statements before P2 or P3 starts. The next two bits, 10, mean that P2 must run after P1 has started but before P3 has started. The last two bits, 01, mean that P3, must complete before P1 starts, but we have already seen that P1 must go first. Therefore, 001001 is not allowed.
In short, the 90 different valid statement orderings produce a variety of different program results (less than 64, though) that are allowed under the assumption of sequential consistency. The contract between the software and memory here is that the software must accept all of these as valid results. In other words, the software must accept the four results shown in Fig. 6-15 and all the other valid results as proper answers, and must work correctly if any of them occurs. A program that works for some of these results and not for others violates the contract with the memory and is incorrect.
A sequentially consistent memory can be implemented on a DSM or multiprocessor system that replicates writable pages by ensuring that no memory operation is started until all the previous ones have been completed. In a system with an efficient, totally-ordered reliable broadcast mechanism, for example, all shared variables could be grouped together on one or more pages, and operations to the shared pages could be broadcast. The exact order in which the operations are interleaved does not matter as long as all processes agree on the order of all operations on the shared memory.
Various formal systems have been proposed for expressing sequential consistency (and other models). Let us briefly consider the system of Ahamad et al. (1993). In their method, the sequence of read and write operations of process i is designated by Hi, (the history of Pi). Figure 6-12(b) shows two such sequences, H1 and H2 for P1 and P2, respectively, as follows:
H1=W(x)1
H2=R(x)0 R(x)1
The set of all such sequences is called H.
To get the relative order in which the operations appear to be executed, we must merge the operation strings in H into a single string, S, in which each operation appearing in H appears in S once. Intuitively, S gives the order that the operations would have been carried out had there been a single centralized memory. All legal values for S must obey two constraints:
1. Program order must be maintained.
2. Memory coherence must be respected.
The first constraint means that if a read or write access, A, appears before another access, B, in one of the strings in H, A must also appear before B in S. If this constraint is true for all pairs of operations, the resulting S will not show any operations in an order that violates any of the programs.
The second constraint, called memory coherence, means that a read to some location, x, must always return the value most recently written to x; that is, the value v written by the most recent W(x)v before the R(x). Memory coherence examines in isolation each location and the sequence of operations on it, without regard to other locations. Consistency, in contrast, deals with writes to different locations and their ordering.
For Fig. 6-12(b) there is only one legal value of S:
S=R(x)0 W(x)1 R(x)1,
For more complicated examples there might be several legal values of S. The behavior of a program is said to be correct if its operation sequence corresponds to some legal value of S.
Although sequential consistency is a programmer-friendly model, it has a serious performance problem. Lipton and Sandberg (1988) proved that if the read time is r, the write time is w, and the minimal packet transfer time between nodes is t, then it is always true that r+w?t. In other words, for any sequentially consistent memory, changing the protocol to improve the read performance makes the write performance worse, and vice versa. For this reason, researchers have investigated other (weaker) models. In the following sections we will discuss some of them.




