Книга: Distributed operating systems

4.6.4. Real-Time Scheduling

4.6.4. Real-Time Scheduling

Real-time systems are frequently programmed as a collection of short tasks (processes or threads), each with a well-defined function and a well-bounded execution time. The response to a given stimulus may require multiple tasks to be run, generally with constraints on their execution order. In addition, a decision has to be made about which tasks to run on which processors. In this section we will deal with some of the issues concerning task scheduling in real-time systems.

Real-time scheduling algorithms can be characterized by the following parameters:

1. Hard real time versus soft real time.

2. Preemptive versus nonpreemptive scheduling.

3. Dynamic versus static.

4. Centralized versus decentralized.

Hard real-time algorithms must guarantee that all deadlines are met. Soft realtime algorithms can live with a best efforts approach. The most important case is hard real time.

Preemptive scheduling allows a task to be suspended temporarily when a higher-priority task arrives, resuming it later when no higher-priority tasks are available to run. Nonpreemptive scheduling runs each task to completion. Once a task is started, it continues to hold its processor until it is done. Both kinds of scheduling strategies are used.

Dynamic algorithms make their scheduling decisions during execution. When an event is detected, a dynamic preemptive algorithm decides on the spot whether to run the (first) task associated with the event or to continue running the current task. A dynamic nonpreemptive algorithm just notes that another task is runnable. When the current task finishes, a choice among the now-ready tasks is made.

With static algorithms, in contrast, the scheduling decisions, whether preemptive or not, are made in advance, before execution. When an event occurs, the runtime scheduler just looks in a table to see what to do.

Finally, scheduling can be centralized, with one machine collecting all the information and making all the decisions, or it can be decentralized, with each processor making its own decisions. In the centralized case, the assignment of tasks to processors can be made at the same time. In the decentralized case, assigning tasks to processors is distinct from deciding which of the tasks assigned to a given processor to run next.

A key question that all real-time system designers face is whether or not it is even possible to meet all the constraints. If a system has one processor and it gets 60 interrupts/sec, each requiring 50 msec of work, the designers have a Big Problem on their hands.

Suppose that a periodic real-time distributed system has m tasks and N processors to run them on.  Let C_i be the CPU time needed by task i, and let P_i be its period, that is, the time between consecutive interrupts. To be feasible, the utilization of the system, µ, must be related to N by the equation

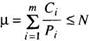
For example, if a task is started every 20 msec and runs for 10 msec each time, it uses up 0.5 CPUs. Five such tasks would need three CPUs to do the job. A set of tasks that meets the foregoing requirement is said to be schedulable. Note that the equation above really gives a lower bound on the number of CPUs needed, since it ignores task switching time, message transport, and other sources of overhead, and assumes that optimal scheduling is possible.

In the following two sections we will look at dynamic and static scheduling, respectively, of sets of periodic tasks. For additional information, see (Ramam-ritham et al., 1990; and Schwan and Zhou, 1992).

Let us look first at a few of the better-known dynamic scheduling algorithms — algorithms that decide during program execution which task to run next. The classic algorithm is the rate monotonic algorithm (Liu and Layland, 1973). it was designed for preemptively scheduling periodic tasks with no ordering or mutual exclusion constraints on a single processor. It works like this. In advance, each task is assigned a priority equal to its execution frequency. For example, a task run every 20 msec is assigned priority 50 and a task run every 100 msec is assigned priority 10. At run time, the scheduler always selects the highest priority task to run, preempting the current task if need be. Liu and Lay-land proved that this algorithm is optimal. They also proved that any set of tasks meeting the utilization condition

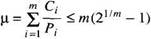
is schedulable using the rate monotonic algorithm. The right-hand side converges to ln2 (about 0.693) as m??. In practice, this limit is overly pessimistic; a set of tasks with µ as high as 0.88 can usually be scheduled.

A second popular preemptive dynamic algorithm is earliest deadline first. Whenever an event is detected, the scheduler adds it to the list of waiting tasks. This list is always keep sorted by deadline, closest deadline first. (For a periodic task, the deadline is the next occurrence.) The scheduler then just chooses the first task on the list, the one closest to its deadline. Like the rate monotonic algorithm, it produces optimal results, even for task sets with µ=1.

A third preemptive dynamic algorithm first computes for each task the amount of time it has to spare, called the laxity (slack). For a task that must finish in 200 msec but has another 150 msec to run, the laxity is 50 msec. This algorithm, called least laxity, chooses the task with the least laxity, that is, the one with the least breathing room.

None of the algorithms above are provably optimal in a distributed system, but they can be used as heuristics. Also, none of them takes into account order or mutex constraints, even on a uniprocessor, which makes them less useful in practice than they are in theory. Consequently, many practical systems use static scheduling when enough information is available. Not only can static algorithms take side constraints into account, but they have very low overhead at run time.

Static scheduling is done before the system starts operating. The input consists of a list of all the tasks and the times that each must run. The goal is to find an assignment of tasks to processors and for each processor, a static schedule giving the order in which the tasks are to be run. In theory, the scheduling algorithm can run an exhaustive search to find the optimal solution, but the search time is exponential in the number of tasks (Ullman, 1976), so heuristics of the type described above are generally used. Rather than simply give some additional heuristics here, we will go into one example in detail, to show the interplay of scheduling and communication in a real-time distributed system with nonpreemptive static scheduling (Kopetz et al., 1989).

Let us assume that every time a certain event is detected, task 1 is started on processor A, as shown in Fig. 4-30. This task, in turn, starts up additional tasks, both locally and on a second processor, B. For simplicity, we will assume that the assignment of tasks to processors is dictated by external considerations (which task needs access to which I/O device) and is not a parameter here. All tasks take 1 unit of CPU time.

Task 1 starts up tasks 2 and 3 on its machine, as well as task 7 on processor B. Each of these three tasks starts up another task, and so on, as illustrated. The arrows indicate messages being sent between tasks. In this simple example, it is perhaps easiest to think of X?Y as meaning that Y cannot start until a message from X has arrived. Some tasks, such as 8, require two messages before they may start. The cycle is completed when task 10 has run and generated the expected response to the initial stimulus.

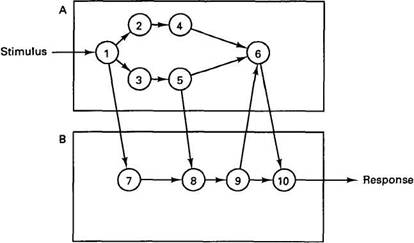
Fig. 4-30. Ten real-time tasks to be executed on two processors.

After task 1 has completed, tasks 2 and 3 are both runnable. The scheduler has a choice of which one to schedule next. Suppose that it decides to schedule task 2 next. It then has a choice between tasks 3 and 4 as the successor to task 2. If it chooses task 3, it then has a choice between tasks 4 and 5 next. However, if it chooses 4 instead of 3, it must run 3 following 4, because 6 is not enabled yet, and will not be until both 5 and 9 have run.

Meanwhile, activity is also occurring in parallel on processor B. As soon as task 1 has initiated it, task 7 can start on B, at the same time as either 2 or 3. When both 5 and 7 have finished, task 8 can be started, and so on. Note that task 6 requires input from 4, 5, and 9 to start, and produces output for 10.

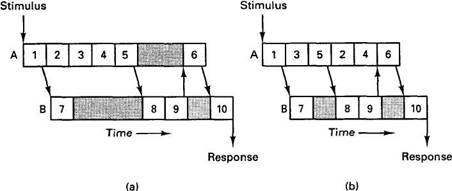
Fig. 4-31. Two possible schedules for the tasks of Fig. 4-30.

Two potential schedules are given in Fig. 4-31(a) and (b). Messages between tasks on different processors are depicted as arrows here; messages between tasks on the same machine are handled internally and are not shown. Of the two schedules illustrated, the one in Fig. 4-31(b) is a better choice because it allows task 5 to run early, thus making it possible for task 8 to start earlier. If task 5 is delayed significantly, as in Fig. 4-31(a), then tasks 8 and 9 are delayed, which also means that 6 and eventually 10 are delayed, too.

It is important to realize that with static scheduling, the decision of whether to use one of these schedules, or one of several alternatives is made by the scheduler in advance, before the system starts running. It analyzes the graph of Fig. 4-30, also using as input information about the running times of all the tasks, and then applies some heuristic to find a good schedule. Once a schedule has been selected, the choices made are incorporated into tables so that at run time a simple dispatcher can carry out the schedule with little overhead.

Now let us consider the problem of scheduling the same tasks again, but this time taking communication into account. We will use TDMA communication, with eight slots per TDMA frame. In this example, a TDMA slot is equal to one-fourth of a task execution time. We will arbitrarily assign slot 1 to processor A and slot 5 to processor B. The assignment of TDMA slots to processors is up to the static scheduler and may differ between program phases.

In Fig. 4-32 we show both schedules of Fig. 4-31, but now taking the use of TDMA slots into account. A task may not send a message until a slot owned by its processor comes up. Thus, task 5 may not send to task 8 until the first slot of the next TDMA frame occurs in rotation, requiring a delay in starting task 8 in Fig. 4-32(a) that was not present before.

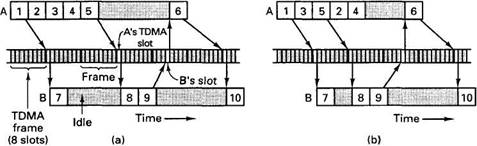
Fig. 4-32. Two schedules, including processing and communication.

The important thing to notice about this example is that the runtime behavior is completely deterministic, and known even before the program starts executing. As long as communication and processor errors do not occur, the system will always meet its real-time deadlines. Processor failures can be masked by having each node consist of two or more CPUs actively tracking each other. Some extra time may have to be statically allocated to each task interval to allow for recovery, if need be. Lost or garbled packets can be handled by having every one sent twice initially, either on disjoint networks or on one network by making the TDMA slots two packets wide.

It should be clear by now that real-time systems do not try to squeeze the last drop of performance out of the hardware, but rather use extra resources to make sure that the real-time constraints are met under all conditions. However, the relatively low use of the communication bandwidth in our example is not typical. It is a consequence of this example using only two processors with modest communication requirements. Practical real-time systems have many processors and extensive communication.

The choice of dynamic or static scheduling is an important one and has far-reaching consequences for the system. Static scheduling is a good fit with a time-triggered design, and dynamic scheduling is a good fit for an event-triggered design. Static scheduling must be carefully planned in advance, with considerable effort going into choosing the various parameters. Dynamic scheduling does not require as much advance work, since scheduling decisions are made on-the-fly, during execution.

Dynamic scheduling can potentially make better use of resources than static scheduling. In the latter, the system must frequently be overdimensioned to have so much capacity that it can handle even the most unlikely cases. However, in a hard real-time system, wasting resources is often the price that must be paid to guarantee that all deadlines will be met.

On the other hand, given enough computing power, an optimal or nearly optimal schedule can be derived in advance for a static system. For an application such as reactor control, it may well be worth investing months of CPU time to find the best schedule. A dynamic system cannot afford the luxury of a complex scheduling calculation during execution, so to be safe, may have to be heavily overdimensioned as well, and even then, there is no guarantee that it will meet its specifications. Instead, extensive testing is required.

As a final thought, it should be pointed out that our discussion has simplified matters considerably. For example, tasks may need access to shared variables, so these have to be reserved in advance. Often there are scheduling constraints, which we have ignored. Finally, some systems do advance planning during runtime, making them hybrids between static and dynamic.

Оглавление книги