Книга: Distributed operating systems

4.3.4. Example Processor Allocation Algorithms

4.3.4. Example Processor Allocation Algorithms

To provide insight into how processor allocation can really be accomplished, in this section we will discuss several different algorithms. These have been selected to cover a broad range of possibilities, but there are others as well.

A widely-studied class of algorithm is for systems consisting of processes with known CPU and memory requirements, and a known matrix giving the average amount of traffic between each pair of processes. If the number of CPUs, k, is smaller than the number of processes, several processes will have to be assigned to each CPU. The idea is to perform this assignment such as to minimize network traffic.

The system can be represented as a weighted graph, with each node being a process and each arc representing the flow of messages between two processes. Mathematically, the problem then reduces to finding a way to partition (i.e., cut) the graph into k disjoint subgraphs, subject to certain constraints (e.g., total CPU and memory requirements below some limits for each subgraph). For each solution that meets the constraints, arcs that are entirely within a single subgraph represent intramachine communication and can be ignored. Arcs that go from one subgraph to another represent network traffic. The goal is then to find the partitioning that minimizes the network traffic while meeting all the constraints. Figure 4-17 shows two ways of partitioning the same graph, yielding two different network loads.

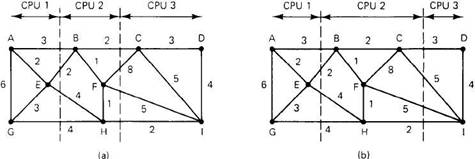
Fig. 4-17. Two ways of allocating nine processes to three processors.

In Fig. 4-17(a), we have partitioned the graph with processes A, E, and G on one processor, processes B, F, and H on a second, and processes C, D, and I on the third. The total network traffic is the sum of the arcs intersected by the dotted cut lines, or 30 units. In Fig. 4-17(b) we have a different partitioning that has only 28 units of network traffic. Assuming that it meets all the memory and CPU constraints, this is a better choice because it requires less communication.

Intuitively, what we are doing is looking for clusters that are tightly coupled (high intracluster traffic flow) but which interact little with other clusters (low intercluster traffic flow). Some of the many papers discussing the problem are (Chow and Abraham, 1982; Stone and Bokhari, 1978; and Lo, 1984).

Graph-theoretic algorithms of the kind we have just discussed are of limited applicability since they require complete information in advance, so let us turn to a heuristic algorithm that does not require any advance information. This algorithm, called up-down (Mutka and Livny, 1987), is centralized in the sense that a coordinator maintains a usage table with one entry per personal workstation (i.e., per user), initially zero. when significant events happen, messages are sent to the coordinator to update the table. Allocation decisions are based on the table. These decisions are made when scheduling events happen: a processor is being requested, a processor has become free, or the clock has ticked.

The unusual thing about this algorithm, and the reason that it is centralized, is that instead of trying to maximize CPU utilization, it is concerned with giving each workstation owner a fair share of the computing power. Whereas other algorithms will happily let one user take over all the machines if he promises to keep them all busy (i.e., achieve a high CPU utilization), this algorithm is designed to prevent precisely that.

When a process is to be created, and the machine it is created on decides that the process should be run elsewhere, it asks the usage table coordinator to allocate it a processor. If there is one available and no one else wants it, the request is granted. If no processors are free, the request is temporarily denied and a note is made of the request.

When a workstation owner is running processes on other people's machines, it accumulates penalty points, a fixed number per second, as shown in Fig. 4-18. These points are added to its usage table entry. When it has unsatisfied requests pending, penalty points are subtracted from its usage table entry. When no requests are pending and no processors are being used, the usage table entry is moved a certain number of points closer to zero, until it gets there. In this way, the score goes up and down, hence the name of the algorithm.

Usage table entries can be positive, zero, or negative. A positive score indicates that the workstation is a net user of system resources, whereas a negative score means that it needs resources. A zero score is neutral.

The heuristic used for processor allocation can now be given. When a processor becomes free, the pending request whose owner has the lowest score wins. As a consequence, a user who is occupying no processors and who has had a request pending for a long time will always beat someone who is using many processors. This property is the intention of the algorithm, to allocate capacity fairly.

In practice this means that if one user has a fairly continuous load on the system, and another user comes along and wants to start a process, the light user will be favored over the heavy one. Simulation studies (Mutka and Livny, 1987) show that the algorithm works as expected under a variety of load conditions.

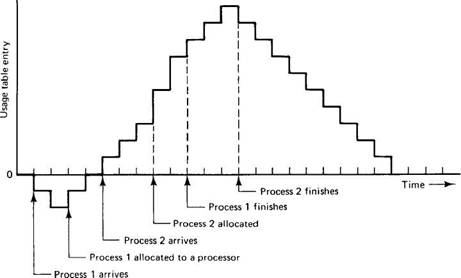
Fig. 4-18. Operation of the up-down algorithm.

Centralized algorithms, such as up-down, do not scale well to large systems. The central node soon becomes a bottleneck, not to mention a single point of failure. These problems can be attacked by using a hierarchical algorithm instead of a centralized one. Hierarchical algorithms retain much of the simplicity of centralized ones, but scale better.

One approach that has been proposed for keeping tabs on a collection of processors is to organize them in a logical hierarchy independent of the physical structure of the network, as in MICROS (Wittie and van Tilborg, 1980). This approach organizes the machines like people in corporate, military, academic, and other real-world hierarchies. Some of the machines are workers and others are managers.

For each group of k workers, one manager machine (the "department head") is assigned the task of keeping track of who is busy and who is idle. If the system is large, there will be an unwieldy number of department heads, so some machines will function as "deans," each riding herd on some number of department heads. If there are many deans, they too can be organized hierarchically, with a "big cheese" keeping tabs on a collection of deans. This hierarchy can be extended ad infinitum, with the number of levels needed growing logarithmically with the number of workers. Since each processor need only maintain communication with one superior and a few subordinates, the information stream is manageable.

An obvious question is: What happens when a department head, or worse yet, a big cheese, stops functioning (crashes)? One answer is to promote one of the direct subordinates of the faulty manager to fill in for the boss. The choice of which can be made by the subordinates themselves, by the deceased's peers, or in a more autocratic system, by the sick manager's boss.

To avoid having a single (vulnerable) manager at the top of the tree, one can truncate the tree at the top and have a committee as the ultimate authority, as shown in Fig. 4-19. When a member of the ruling committee malfunctions, the remaining members promote someone one level down as replacement.

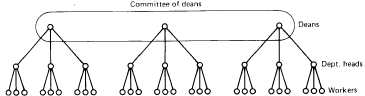
Fig. 4-19. A processor hierarchy can be modeled as an organizational hierarchy.

While this scheme is not really distributed, it is feasible, and in practice works well. In particular, the system is self-repairing and can survive occasional crashes of both workers and managers without any long-term effects.

In MICROS, the processors are monoprogrammed, so if a job requiring S processes suddenly appears, the system must allocate 5 processors for it. Jobs can be created at any level of the hierarchy. The strategy used is for each manager to keep track of approximately how many workers below it are available (possibly several levels below it). If it thinks that a sufficient number are available, it reserves some number R of them, where R>S, because the estimate of available workers may not be exact and some machines may be down.

If the manager receiving the request thinks that it has too few processors available, it passes the request upward in the tree to its boss. If the boss cannot handle it either, the request continues propagating upward until it reaches a level that has enough available workers at its disposal. At that point, the manager splits the request into parts and parcels them out among the managers below it, which then do the same thing until the wave of allocation requests hits bottom. At the bottom level, the processors are marked as "busy" and the actual number of processors allocated is reported back up the tree.

To make this strategy work well, R must be large enough that the probability is high that enough workers will be found to handle the entire job. Otherwise the request will have to move up one level in the tree and start all over, wasting considerable time and computing power. On the other hand, if R is too large, too many processors will be allocated, wasting computing capacity until word gets back to the top and they can be released.

The whole situation is greatly complicated by the fact that requests for processors can be generated randomly anywhere in the system, so at any instant, multiple requests are likely to be in various stages of the allocation algorithm, potentially giving rise to out-of-date estimates of available workers, race conditions, deadlocks, and more. In Van Tilborg and Wittie (1981) a mathematical analysis of the problem is given and various other aspects not described here are covered in detail.

The algorithms described above are all centralized or semicentralized. Distributed algorithms also exist. Typical of these are the ones described by Eager et al. (1986). As mentioned above, in the most cost-effective algorithm they studied, when a process is created, the machine on which it originates sends probe messages to a randomly-chosen machine, asking if its load is below some threshold value. If so, the process is sent there. If not, another machine is chosen for probing. Probing does not go on forever. If no suitable host is found within N probes, the algorithm terminates and the process runs on the originating machine.

An analytical queueing model of this algorithm has been constructed and investigated. Using this model, it was established that the algorithm behaves well and is stable under a wide range of parameters, including different threshold values, transfer costs, and probe limits.

Nevertheless, it should be observed that under conditions of heavy load, all machines will constantly send probes to other machines in a futile attempt to find one that is willing to accept more work. Few processes will be off-loaded, but considerable overhead may be incurred in the attempt to do so.

A complementary algorithm to the one given above, which is initiated by an overloaded sender, is one initiated by an underloaded receiver. With this algorithm, whenever a process finishes, the system checks to see if it has enough work. If not, it picks some machine at random and asks it for work. If that machine has nothing to offer, a second, and then a third machine is asked. If no work is found with N probes, the receiver temporarily stops asking, does any work it has queued up, and tries again when the next process finishes. If no work is available, the machine goes idle. After some fixed time interval, it begins probing again.

An advantage of this algorithm is that it does not put extra load on the system at critical times. The sender-initiated algorithm makes large numbers of probes precisely when the system can least tolerate it — when it is heavily loaded. With the receiver-initiated algorithm, when the system is heavily loaded, the chance of a machine having insufficient work is small, but when this does happen, it will be easy to find work to take over. Of course, when there is little work to do, the receiver-initiated algorithm, creates considerable probe traffic as all the unemployed machines desperately hunt for work. However, it is far better to have the overhead go up when the system is underloaded than when it is overloaded.

It is also possible to combine both of these algorithms and have machines try to get rid of work when they have too much, and try to acquire work when they do not have enough. Furthermore, machines can perhaps improve on random polling by keeping a history of past probes to determine if any machines are chronically underloaded or overloaded. One of these can be tried first, depending on whether the initiator is trying to get rid of work or acquire it.

Another class of algorithms tries to turn the computer system into a miniature economy, with buyers and sellers of services and prices set by supply and demand (Ferguson et al., 1988). The key players in the economy are the processes, which must buy CPU time to get their work done, and processors, which auction their cycles off to the highest bidder.

Each processor advertises its approximate price by putting it in a publicly readable file. This price is not guaranteed, but gives an indication of what the service is worth (actually, it is the price that the last customer paid). Different processors may have different prices, depending on their speed, memory size, presence of floating-point hardware, and other features. An indication of the service provided, such as expected response time, can also be published.

When a process wants to start up a child process, it goes around and checks out who is currently offering the service that it needs. It then determines the set of processors whose services it can afford. From this set, it computes the best candidate, where "best" may mean cheapest, fastest, or best price/performance, depending on the application. It then generates a bid and sends the bid to its first choice. The bid may be higher or lower than the advertised price.

Processors collect all the bids sent to them, and make a choice, presumably by picking the highest one. The winners and losers are informed, and the winning process is executed. The published price of the server is then updated to reflect the new going rate.

Although Ferguson et al. do not go into the details, such an economic model raises all kinds of interesting questions, among them the following. Where do processes get money to bid? Do they get regular salaries? Does everyone get the same monthly salary, or do deans get more than professors, who in turn get more than students? If new users are introduced into the system without a corresponding increase in resources, do prices get bid up (inflation)? Can processors form cartels to gouge users? Are users' unions allowed? Is disk space also chargeable? How about laser printer output? The list goes on and on.

Оглавление книги