Книга: ПРОГРАММИРОВАНИЕ НА ЯЗЫКЕ ПРОЛОГ

4.3.1. Подтверждение правильности выбора правила

4.3.1. Подтверждение правильности выбора правила

При программировании на Прологе очень часто возникает желание использовать для описания одного предиката несколько утверждений. Одно утверждение будет использоваться, если аргументы имеют один вид, другое будет использоваться для аргументов иного вида и так далее. Часто мы можем указать, какое правило следует использовать для данного целевого утверждения, указав в качестве аргументов в заголовке правила необходимые образцы структур так, чтобы это правило могло быть сопоставлено лишь с соответствующими целевыми утверждениями. Однако это не всегда возможно. Если мы не можем сказать заранее, какого вида аргументы будут использоваться, или если мы не можем перечислить все множество возможных образцов аргументов, то мы можем принять компромиссное решение. Это значит, что задаются правила для аргументов определенных типов, а в конце задается правило-«ловушка» для всех остальных правил. В качестве примера такого способа рассмотрим следующую программу. Определим предикат сумма таким образом, что при выборе в качестве целевого утверждения сумма(N, X), где N – некоторое целое число, переменной X присваивается значение, равное сумме всех целых чисел от 1 до N. Так, например, возможен следующий диалог:

?- сумма(5,X).

X = 15;

нет

Полученный ответ объясняется тем, что 1+2+3+4+5 равно 15. Здесь приведена соответствующая программа.

сумма(1,1):-!.

сумма(N,Результат):- N1 is N-1, сумма(N1,Результат),Результат is Результат+N.

Приведенное определение является рекурсивным. Идея состоит в том, что выход на граничное условие происходит в случае, когда первый аргумент равен 1. В этом случае ответ тоже равен 1. Второе утверждение вводит рекурсивное целевое утверждение сумма. Однако первый аргумент нового целевого утверждения на единицу меньше, чем первый аргумент в исходном целевом утверждении. Следующее целевое утверждение, которое будет порождено этим целевым утверждением, снова будет иметь первый аргумент на единицу меньше. И так далее до тех пор, пока не будет достигнуто граничное условие. Так как первый аргумент всегда на единицу меньше, то в конце концов произойдет выход на граничное условие (в предположении, что исходное целевое утверждение имеет первый аргумент не меньше 1) и выполнение программы закончится.

Представляет интерес то, как в этой программе организована обработка двух случаев: когда число, соответствующее первому аргументу, равно 1 и когда оно отлично от 1. Когда мы определяли предикаты для обработки списков, то было легко указать два типичных случая: когда список был пустым ([]) и когда он имел вид [A|B]. Для чисел это не так просто сделать, потому что мы не можем задать такой аргумент, который был бы сопоставим только с целым числом, не равным 1. Приемлемое решение в данном примере состоит в том, чтобы выделить случай, когда первый аргумент равен 1, и обеспечить сопоставление для всех остальных случаев с помощью переменной. Мы знаем, что в соответствии со стратегией, используемой при поиске в базе данных, Пролог сначала будет пытаться произвести сопоставление с правилом для 1, и только в случае неудачи он попытается использовать второе правило. Таким образом, второе правило используется только для чисел, не равных 1. Но этим дело не кончается. Если когда-либо Пролог будет выполнять возврат и попытается пересмотреть выбор правила с первым аргументом, равным 1, то он обнаружит, что второе правило тоже применимо. Как можно видеть, оба правила являются альтернативными для целевого утверждения сумма(1,X). Мы должны указать Прологу, что ни в коем случае не следует использовать второе правило, если число, соответствующее первому аргументу, равно 1. Один из способов сделать это – вставить отсечение в первое правило (как это и показано в записи этого правила). Это отсечение указывает Прологу, что если выбрано первое правило, то больше не следует принимать нового решения относительно того, какое правило использовать для целевого утверждения сумма. В случае если число, соответствующее первому аргументу, действительно равно 1, может произойти только выбор первого правила.

Давайте посмотрим, как все это выглядит на языке диаграмм. Если мы обратимся к предикату сумма(1,X) в следующем контексте:

выполнить:- сумма(1,X), foo(apples)

?-выполнить.

и для цели foo(apples) нет сопоставления, то к моменту, когда обнаружится несогласованность foo(apples) с базой данных, результат работы Пролога будет иметь вид, как показано на рис. 4.6. Если Пролог попытается найти новые сопоставления для целевых утверждений, просматривая их в обратном порядке, то обнаружится, что рассмотренные выше два альтернативных целевых утверждения не могут быть пересмотрены, так как они исключены из цепочки доказательства. Следовательно, наиболее верный путь – не пытаться найти другое сопоставление для предиката сумма(1,X).

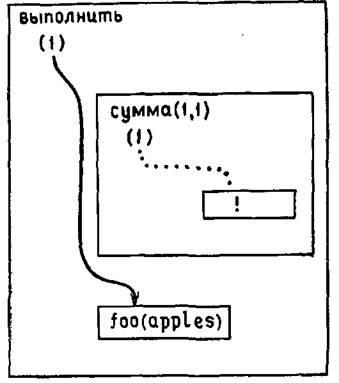
Рис. 4.6.

Упражнение 4.1. Что произойдет в процессе возврата при попытке найти новое сопоставление для целевогоутверждения сумма, если из первого правила для предиката сумма удалить отсечение? Какие альтернативные результаты будут получены (если вообще они будут возможны) и почему?

Последний пример показал, как можно использовать отсечение для того, чтобы сделать поведение Пролога чувствительным к случаю, когда мы не можем выделить все возможные случаи путем перечисления образцов в заголовках правил. Более типичная ситуация, в которой мы не можем указать структуру заголовков правил для выполнения сопоставления, возникает, если мы хотим ввести дополнительные условия в виде целевых утверждений Пролога, позволяющих в процессе согласования с базой данных выбрать соответствующие правила. Рассмотрим следующий альтернативный вариант решения последнего примера:

сумма(N,1):- N =‹ 1,!.

cyммa(N,R):- N1 is N-1, сумма(N1,R1), R is Rl+N

В этом случае указывается, что первое правило следует выбрать, когда заданное количество суммируемых чисел меньше или равно единице. Такое определение правила немного лучше, чем предыдущее, потому что соответствующая ему программа даст ответ (вместо того чтобы выполняться бесконечно), если в качестве первого аргумента будет задан 0 или отрицательное число. Если условие первого правила выполняется, то сразу же выдается результат 1 и не требуется прибегать к рекурсивному порождению целевых утверждений. Второе правило следует попытаться использовать лишь в случае, когда это условие не выполняется. Мы должны указать Прологу, что если уже обнаружено, что N = ‹ 1, то не следует возвращаться к пересмотру выбора правила. Это как раз и достигается с помощью отсечения.

Общий принцип заключается в том, что использование механизма отсечения для указания Прологу на ситуации, когда он выбрал единственно правильное правило, может быть заменено использованием предиката not. Это встроенный предикат Пролога, т. е. определение этого предиката заранее известно Пролог-системе. Поэтому его можно использовать, не выписывая каждый раз его определение (более полно встроенные предикаты описываются в гл. 6). Предикат not определен таким образом, что целевое утверждение not(X) истинно, только если X, рассматриваемое как целевое утверждение, не согласуется с базой данных. Таким образом, not(X) означает, что X недоказуемо как целевое утверждение Пролога, т. е. не согласовано с базой данных. В качестве примера использования not вместо отсечения перепишем два варианта определения предиката сумма следующим образом:

сумма(1,1).

cyммa(N,R):- not(N = 1), N1 is N-1, cyммa(N1,R1),R is N1 + R1.

или

сумма(N,1):- N =‹1.

сумма(N,R):- not(N=‹l), N1 is N-1, сумма(N1,R1),R is N1 + R1.

В действительности в Прологе имеются другие удобные встроенные предикаты, которые могут заменить оба из приведенных вхождений предиката not. Например, можно заменить not(N=1) на N=1, a not(N =‹ 1) на N›1. В общем случае это можно сделать не со всеми возможными условиями.

Использование предиката not вместо отсечения свойственно для хорошего стиля программирования. Это связано с тем, что программы, содержащие отсечения, как правило, более трудны для чтения, чем программы, не содержащие их. Если удается локализовать все вхождения отсечения и заменить их с помощью предиката not, то программа станет более понятной. Однако определение not предполагает попытку доказать, что заданное целевое утверждение согласуется с базой данных. Поэтому если мы имеем программу, в общем виде представимую как

A:-B, C

A:-not(B),D

то Прологу для успешного завершения программы может потребоваться две попытки согласовать B. Он должен попытаться согласовать B при просмотре первого правила. Но если затем будет выполнен возврат и рассмотрено второе правило, то он будет вынужден попытаться согласовать B вновь, чтобы убедиться, может ли быть согласовано not(B). Такое дублирование приводит к потере эффективности программы, когда условие B достаточно сложно. Этого бы не произошло, если бы вместо приведенной программы мы имели:

A:-B,!,C

A:-D

Таким образом, иногда нужно взвесить преимущества ясной программы по сравнению с преимуществами ее быстрого выполнения. Обсуждение вопроса эффективности приводит нас к последнему примеру, в котором отсечение используется для фиксирования выбора правила. Рассмотрим определение предиката присоединить:

присоединить([],X,X).

присоединить([А|В],С,[А|D]) – присоединить(В,С,D).

Если предикат присоединить используется лишь в случаях, когда, имея два списка, мы хотим найти список, получающийся в результате добавления элементов второго списка в конец первого, то такая программа неэффективна, поскольку, если выполняется возврат при обработке целевого утверждения вида присоединить([],[a,b,c,d],X), Пролог обязан сделать попытку использовать второе правило, несмотря на то что эта попытка заранее обречена на неудачу. В таком контексте пустота первого списка указывает на то, что первое правило является единственным возможным для использования и эта информация может быть сообщена Прологу с помощью отсечения. В общем случае при применениях Пролог-системы смогут лучше использовать имеющуюся память, если сообщать системе такие сведения, по сравнению с тем, когда она должна хранить информацию о выборе правил, которая в действительности использована не будет. Можно с этой целью переписать наше определение следующим образом:

присоединить([],X,X):-!.

присоединить([А|В],С,[А|D]:- присоединить(В,С,D).

При сделанных предположениях относительно применения предиката присоединить это никак не повлияет на то, какие решения найдет программа, но несколько повысит ее эффективность по времени выполнения и объему занятой памяти. В качестве платы за это мы потеряли возможность использования предиката присоединить в других ситуациях – он больше не будет работать ожидаемым образом, что будет показано в разд. 4.4.

Оглавление книги