Книга: Базы данных: конспект лекций

2. Правила вывода Армстронга

2. Правила вывода Армстронга

Если какое-либо базовое отношение удовлетворяет векторно определенным функциональным зависимостям, то с помощью различных специальных правил вывода можно получить другие функциональные зависимости, которым данное базовое отношение будет заведомо удовлетворять.

Хорошим примером таких специальных правил являются правила вывода Армстронга.

Но прежде чем приступать к анализу самих правил вывода Армстронга, введем в рассмотрение новый металингвистический символ «?», который называется символом метаутверждения о выводимости. Этот символ при формулировании правил записывается между двумя синтаксическими выражениями и свидетельствует о том, что из формулы, стоящей слева от него, выводится формула, стоящая справа от него.

Сформулируем теперь сами правила вывода Армстронга в виде следующей теоремы.

Теорема. Справедливы следующие правила, называемые правилами вывода Армстронга.

Правило вывода 1. ? X ? X;

Правило вывода 2. X ? Y? X ? Z ? Y;

Правило вывода 3. X ? Y, Y ? W ? Z ? X ? W ? Z;

Здесь X, Y, Z, W – произвольные подсхемы схемы отношения S. Символ метаутверждения о выводимости разделяет списки посылок и списки утверждений (заключений).

1. Первое правило вывода называется «рефлексивность» и читается следующим образом: «выводится правило: “X функционально влечет за собой X”». Это самое простое из правил вывода Армстронга. Оно выводится буквально из воздуха.

Интересно заметить, что функциональная зависимость, обладающая и левой, и правой частями, называется рефлексивной. Согласно правилу рефлексивности ограничение рефлексивной зависимости выполняется автоматически.

2. Второе правило вывода называется «пополнение» и читается таким образом: «если X функционально определяет Y, то выводится правило: “объединение подсхем X и Z функционально влечет за собой Y”». Правило пополнения позволяет расширять левую часть ограничения функциональных зависимостей.

3. Третье правило вывода называется «псевдотранзитивность» и читается следующим образом: “если подсхема X функционально влечет за собой подсхему Y и объединение подсхем Y и W функционально влекут за собой Z, то выводится правило: «объединение подсхем X и W функционально определяют подсхему Z»”.

Правило псевдотранзитивности обобщает правило транзитивности, соответствующее частному случаю W: = 0. Приведем формулярную запись этого правила:

Необходимо отметить, что посылки и заключения, приведенные ранее, были представлены в сокращенной форме обозначениями схем функциональной зависимости. В расширенной форме им соответствуют следующие ограничения функциональных зависимостей.

Правило вывода 1. inv <X ? X> r(S);

Правило вывода 2. inv <X ? Y> r(S) ? inv <X ? Z ? Y> r(S);

Правило вывода 3. inv <X ? Y> r(S) & inv <Y ? W ? Z> r(S) ? inv<X ? W ? Z> r(S);

Проведем доказательства этих правил вывода.

1. Доказательство правила рефлексивности следует непосредственно из определения ограничения функциональной зависимости при подстановке вместо подсхемы Y – подсхемы X.

Действительно, возьмем ограничение функциональной зависимости:

Inv <X ? Y> r(S) и подставим в него X вместо Y, получим:

Inv <X ? X> r(S), а это и есть правило рефлексивности.

Правило рефлексивности доказано.

2. Доказательство правила пополнения проиллюстрируем на диаграммах функциональной зависимости.

Первая диаграмма – это диаграмма посылки:

посылка: X ? Y

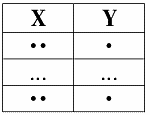
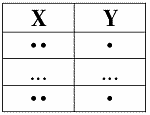
Вторая диаграмма:

заключение: X ? Z ? Y

Пусть кортежи равны на X ? Z. Тогда они равны на X. Согласно посылке они будут равны и на Y.

Правило пополнения доказано.

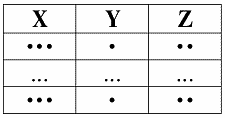
3. Доказательство правила псевдотранзитивности также проиллюстрируем на диаграммах, которых в этом конкретном случае будет три.

Первая диаграмма – первая посылка:

посылка 1: X ? Y

посылка 2: Y ? W ? Z

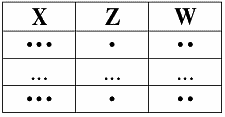
И, наконец, третья диаграмма – диаграмма заключения:

заключение: X ? W ? Z

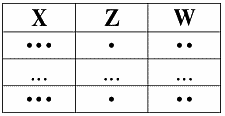
Пусть кортежи равны на X ? W. Тогда они равны и на X, и на W. Согласно Посылке 1, они будут равны и на Y. Отсюда, согласно Посылке 2, они будут равны и на Z.

Правило псевдотранзитивности доказано.

Все правила доказаны.

Оглавление книги