Книга: ПРОГРАММИРОВАНИЕ НА ЯЗЫКЕ ПРОЛОГ

7.12. Отображение структур и преобразование деревьев

7.12. Отображение структур и преобразование деревьев

Если некоторая структура покомпонентно копируется с целью образования новой структуры, то мы говорим, что одна структура отображается в другую. Обычно при копировании каждая компонента слегка изменяется подобно тому, как в гл. 3 мы изменяли одно предложение, превращая его в другое. В том примере нам иногда нужно было скопировать какое-то слово в точности в том виде, в каком оно встретилось в исходном предложении, а иногда при копировании нам нужно было изменить слово. Для этого мы использовали следующую программу, которая отображает первый аргумент предиката преобразовать во второй его аргумент:

преобразовать([],[]).

преобразовать([А|В],[С|D]):- заменить(А,С),преобразовать(В,D).

Поскольку отображение имеет довольно широкое применение, мы можем определить предикат отобспис такой, что целевое утверждение отобспис(Р, L, M) согласуется с базой данных, применяя предикат Р к каждому элементу списка L и образуя в результате новый список М. При этом предполагается, что предикат Р имеет два аргумента: первый аргумент для передачи «входного» элемента, а второй аргумент – для измененного элемента, подлежащего включению в список М.

отобспис((_,[],[]).

отобспис((P,[X|L],[Y|M]):- Q =..[P,X,Y],call(Q),отобспис(Р,L,М).

Об этом определении следует сказать несколько слов. Во-первых, определение содержит граничное условие (первое утверждение) и общий рекурсивный случай (второе утверждение). Во втором утверждении используется оператор '=..', формирующий целевое утверждение на основе предиката (Р), входного элемента (X) и переменной (Y), которую предикат Р должен конкретизировать, чтобы образовать измененный элемент. Затем делается попытка согласовать цель Q, в результате чего Y конкретизируется, образуя голову третьего аргумента данного вызова предиката отобспис. Наконец, рекурсивный вызов отображает хвост первого аргумента в хвост второго.

Функции предиката преобразовать может выполнять предикат отобспис. Полагая, что предикат заменить определен как в гл. 3, такое использование отобспис могло бы выглядеть следующим образом:

?- отобспис(заменить,[уоu,аrе,а,computer],Z).

Z = [i, [am, not], a, computer]

Путем упрощения предиката отобспис получается предикат обрабспис, который просто обрабатывает список, применяя некоторый предикат от одного аргумента к каждому элементу списка. При этом новый список не порождается.

обрабспис(_,[]).

обрабспис(Р,[Х|L]):-Q =…[Р,Х],call(Q),обрабспис(Р,L).

Заметим, что предикат печать_строки из гл. 5 можно было бы заменить запросом вида обрабспис(put, L), где L – это строка, которую нужно напечатать.

Отображение применимо не только к спискам; оно может быть определено для структуры любого вида. Например, рассмотрим арифметическое выражение, составленное из функторов * и +, имеющих по два аргумента. Пусть мы хотим отобразить одно выражение в другое, устраняя при этом все умножения на 1. Это алгебраическое приведение могло быть определено с помощью предиката s такого, что s(Op, L, R,Ans) означает, что выражение, состоящее из операции Ор с левым аргументом L и правым аргументом R приводится к упрощенному выражению Ans. Факты, необходимые для устранения умножений на 1, могли бы выглядеть так (из-за коммутативности умножения нужны два факта):

s(*,X,1,X).

s(*,1,X,X).

Эта таблицы упрощений позволяет нам любое выражение вида 1*Х отобразить в X. Посмотрим, как можно воспользоваться этим в программе.

При приведении выражения Е с помощью такой таблицы упрощений, мы вначале должны привести левый аргумент Е, затем привести правый аргумент Е и, наконец, посмотреть, подходит ли этот приведенный результат под случаи, предусмотренные в нашей таблице. Если это так, то мы порождаем новое выражение в соответствии с указаниями таблицы. В качестве «листьев» дерева, представляющего выражение, фигурируют целые числа или атомы, поэтому для приведения листьев к ним самим в граничном условии мы должны использовать встроенный предикат atomic. Как и выше, мы можем использовать ' =..', чтобы разложить выражение Е на функтор и компоненты;

привести(Е,Е):- atomic(E), 1.

привести(Е,F):-Е =.. [Op,L,R],привести(L,Х),привести(R, Y),s(Op,X,Y,F).

Итак, предикат привести отображает выражение Е в выражение F, используя для этого факты, имеющиеся в таблице упрощений s. А что делать, если невозможны никакие упрощения? Чтобы избежать в этом случае неудачного завершения s(Op,X, Y, F), мы должны поместить в конец каждого раздела таблицы упрощений, относящегося к определенному оператору, правило-ловушку. Приведенная ниже таблица упрощений содержит правила для сложения и умножения. Кроме того, в ней выделены правила-ловушки для каждого вида операций.

s(+,X,0,X).

s(+,0,X,X).

s(+,X,Y,X + Y) /* ловушка для + */

s(*,_,0,0).

s(*,0,_,0).

s(*,1,X,X).

s(*,X,1,X).

s(*,X,Y,X*Y). /* ловушка для * */

При наличии правил-ловушек возникает вопрос о выборе способа упрощения некоторых выражений. Например, если нам дано выражение 3+0, мы можем либо использовать первый факт, либо применить правило-ловушку для +. Благодаря способу упорядочения фактов, прежде чем применить правило-ловушку Пролог всегда будет пытаться применить правила для специальных случаев. Поэтому первое решение, полученное предикатом привести, всегда будет являться действительно упрощенным выражением (если оно возможно). Однако альтернативные решения будут иметь не самый простой вид из всех возможных.

Другое упрощение, используемое при выполнении алгебраических преобразований с помощью ЭВМ, известно как свертка констант. В выражении 3*4+a константы 3 и 4 могут быть «свернуты», что дает в результате выражение 12+а. Правила свертки констант могут быть добавлены в соответствующие места приведенной выше таблицы упрощений. Правило для сложения констант выглядит следующим образом:

s(+,X,Y,Z):- integer(X), integer(Y), Z is X+Y.

Соответствующие правила для других арифметических операций имеют аналогичный вид.

В коммутативных операциях, таких как умножение и деление, указанные выше упрощения могут давать различный эффект на выражениях, которые записаны по-разному, но алгебраически эквивалентны. Например, если правило свертки констант задано для умножения, то предикат привести совершенно правильно преобразует 2*3*а в 6*а, но а*2*3 или 2*а*3 будут преобразовываться в самих себя. Чтобы понять, почему это так, подумайте над тем, как выглядят деревья, представляющие эти выражения (см. рис. 7.4).

В первом дереве самое нижнее умножение 2*3 можно свернуть, получив 6, но во втором дереве нет поддеревьев, которые было бы можно свернуть. Однако, используя коммутативность умножения, можно добавить к таблице следующее правило, которое позволит справиться с данным конкретным случаем:

s(*,X*Y,W,X*Z):- integer(Y), integer(W), Z is Y*W.

Более общая алгебраическая система может быть построена путем простого добавления дополнительных s-утверждений вместо увеличения объема программы для привести.

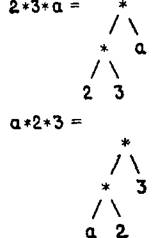
Рис. 7.4

Оглавление книги