Книга: Золотой билет

Первая NP-полная задача

Первая NP-полная задача

В 1970 году Том Хал, глава факультета информатики Университета Торонто, загорелся идеей переманить к себе Стивена Кука, которому не хотели давать постоянное место в Калифорнийском университете в Беркли. Зная любовь Кука к парусному спорту, Хал отвез его на озеро Онтарио: он хотел доказать, что в окрестностях Торонто ходить под парусом почти так же приятно, как и в заливе Сан-Франциско. Хитрость удалась, и осенью 1970 года Кук пополнил ряды специалистов Торонтского университета. Со стороны Хала это был блестящий ход, поскольку в скором времени Кук прославился на весь мир и стал самым известным канадским ученым в области теории вычислений.

Кук проводил исследования на стыке математической логики и теоретической информатики. Той осенью он отправил одну из своих работ на рассмотрение комиссии III Международного симпозиума по теории вычислений (Symposium on the Theory of Computing, сокращенно – STOC), проводимого Ассоциацией вычислительной техники. Симпозиум должен был состояться в мае 1971 года. В статье Кука содержались результаты, полученные им задолго до того и не вызвавшие в свое время ажиотажа. Исследования ученого заинтересовали комиссию, и заявку приняли. К началу конференции Кук почти все переделал; в новой статье, которая называлась The Complexity of Theorem-Proving Procedures, он впервые сформулировал проблему равенства классов P и NP и тем самым полностью изменил ход истории.

Чтобы лучше понять результаты Кука, вернемся к рассмотренной в предыдущей главе задаче о клике. Как вы помните, кликой мы называем группу жителей Королевства, в которой все дружат между собой. На представленной ниже схеме дружеских связей Алекс, Кэти и Эрик образуют клику, а вот Алекс, Дэвид и Эрик – нет, поскольку Алекс не дружит с Дэвидом.

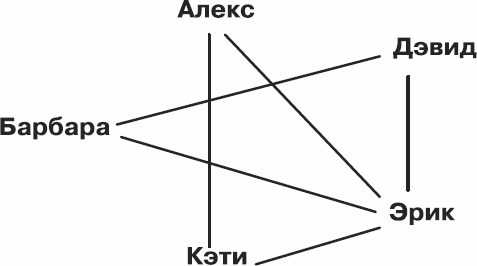
Рис. 4.1. Задача о клике

Мы уже знаем, что в Королевстве есть полусекретное и довольно многочисленное сообщество «Альфа». «Альфовцы» утверждают, что все они дружат между собой, т. е. образуют гигантскую клику. Если это действительно так, то какие сведения можно почерпнуть о них из приведенной выше схемы? Теоретически каждый из пяти может входить в «Альфу». Нельзя исключить вероятность того, что Алекс или Дэвид входят в сообщество, однако они не могут быть там одновременно, поскольку дружбы между ними нет; значит, один из них в сообщество точно не входит. Запишем этот вывод в виде логического выражения:

Алекс не в «Альфе» ИЛИ Дэвид не в «Альфе».

«ИЛИ» здесь не исключающее: возможен вариант, при котором ни Алекс, ни Дэвид не входят в сообщество. Алекс и Барбара тоже враждуют, а следовательно – не могут оба входить в «Альфу». Запишем и это:

Алекс не в «Альфе» ИЛИ Барбара не в «Альфе».

Оба утверждения должны выполняться одновременно, а значит, мы имеем:

(Алекс не в «Альфе» ИЛИ Дэвид не в «Альфе»)

И

(Алекс не в «Альфе» ИЛИ Барбара не в «Альфе»).

Барбара и Дэвид – друзья, поэтому они вполне могут одновременно входить в «Альфу», и построенное нами выражение такой возможности не исключает. Проанализировав всю схему, мы в итоге получим следующее выражение:

(Алекс не в «Альфе» ИЛИ Дэвид не в «Альфе») И (Алекс не в «Альфе» ИЛИ Барбара не в «Альфе») И (Дэвид не в «Альфе» ИЛИ Кэти не в «Альфе») И (Кэти не в «Альфе» ИЛИ Барбара не в «Альфе»).

Допустим, Алекс, Кэти и Эрик принадлежат сообществу, а Барбара и Дэвид – нет; тогда наше выражение истинно, так как в каждом условии «ИЛИ» упоминается кто-то, кто в «Альфу» не входит. Теперь предположим, что сообществу принадлежат Алекс, Дэвид и Эрик. Тогда условие (Алекс не в «Альфе» ИЛИ Дэвид не в «Альфе») не выполняется, поскольку и Алекс, и Дэвид входят в сообщество, а значит – ложно и все выражение.

Наше выражение будет истинно только в том случае, когда все «альфовцы» действительно дружат между собой; с помощью подобных выражений клики отлавливаются очень легко.

Аналогичную конструкцию можно составить и для всех 20 тысяч жителей Королевства. В результате получится огромное, содержащее несколько миллионов символов выражение – впрочем, не настолько длинное, чтобы не уместиться в компьютер. Для краткости обозначим его буквой ?. Очевидно, что ? будет истинно только тогда, когда «альфовцы» в самом деле образуют клику.

Через ?50 обозначим выражение, истинное в том случае, если в «Альфу» входят хотя бы 50 человек. Не будем углубляться в его структуру; достаточно будет сказать, что построить его можно тем же способом, каким первые цифровые компьютеры выполняли сложение чисел.

Соединим наши выражения в одно: (?50 И ?). Если члены сообщества образуют клику размером не меньше 50, то новое выражение примет значение «истина», и наоборот – если выражение истинно, то члены сообщества образуют клику размером не меньше 50.

Логическое выражение, проверяющее принадлежность к сообществу, называется выполнимым, если сообщество можно составить таким образом, что выражение примет значение «истина». Выражение (?50 И ?) выполнимо, когда в сообществе есть клика размера не меньше 50.

Предположим, у нас есть быстрый алгоритм, проверяющий выполнимость логического выражения. Подадим ему на вход выражение (?50 И ?); если алгоритм ответит «да», то в Королевстве существует клика размера 50, а если «нет» – то не существует. Таким образом, алгоритм решения задачи о выполнимости позволяет решить и задачу о клике.

То, чем мы сейчас тут занимались, называется процессом сведения одной задачи к другой. Сведение широко используется в теории сложности, и мы с вами только что свели проблему клики к проблеме выполнимости логического выражения, показав тем самым, что любой метод решения задачи о выполнимости можно применить и к задаче о клике. Появление эффективного алгоритма для задачи о выполнимости означало бы, что такой алгоритм существует и для задачи о клике; найти клику не труднее, чем определить условия выполнимости, и если задачу о выполнимости можно легко решить – значит, задача о клике тоже легко решаема. С другой стороны, если бы кому-то удалось доказать, что для задачи о клике эффективного алгоритма не существует, это означало бы, что его не существует и для задачи о выполнимости.

На самом деле к проблеме выполнимости, или SAT (от англ. satisfiability – выполнимость), сводится не одна лишь задача о клике, но и другие задачи класса NP, которые мы обсуждали ранее, включая задачу о коммивояжере, поиск гамильтонова пути, построение максимального разреза и раскраску карт. Стивен Кук доказал, что любая проблема из NP сводится к проблеме выполнимости. Решите проблему выполнимости – и у вас будет ключ ко всем проблемам из NP. Появление эффективного алгоритма для задачи о выполнимости будет означать, что такой алгоритм существует для всех задач, решение которых легко проверяется, а следовательно, P = NP. Создайте эффективный алгоритм решения проблемы SAT – и получите миллион долларов от Института Клэя!

Сама проблема SAT также принадлежит NP, поскольку для любого набора входных переменных истинность логического выражения проверяется относительно быстро. В классе NP эта задача является универсальной или, как еще говорят, самой трудной, или NP-полной. Доказать наличие эффективного алгоритма для ее решения значит доказать равенство P и NP.

Симпозиум проходил в городке Шейкер-Хайтс в штате Огайо, в отеле Somerset Inn, принадлежащем компании Stouffer. Стивен Кук выступил с докладом 4 мая 1971 года.

«Полученные результаты дают нам основания полагать, что проблема выполнимости – задача чрезвычайно любопытная, поскольку она, по всей видимости, не имеет эффективных методов решения. Думаю, стоит попытаться доказать данную гипотезу: в теории сложности это стало бы величайшим прорывом».

С того дня и ведет свою историю проблема равенства P и NP.

Оглавление книги