Книга: Золотой билет

Линейное программирование

Линейное программирование

Фэнси Франкс продает четыре вида колбасных изделий: франкфуртские сосиски, итальянские сосиски, братвурст и чоризо. У всех продуктов разный состав и время приготовления; все они продаются по разной цене, и стоимость ингредиентов также отличается. Сколько сосисок и колбасок каждого вида должна изготавливать Фэнси, чтобы получать максимальный доход?

Составить оптимальный план выпуска продукции – значит решить задачу максимизации прибыли при ограниченных ресурсах. Пусть фарш для одной франкфуртской сосиски стоит 1 доллар, для итальянской сосиски – 2 доллара, для братвурста – 3 доллара, а для чоризо – 4 доллара, и пусть дневной бюджет по расходам на мясо составляет 10000 долларов. Тогда количество франкфуртских, умноженное на один, плюс количество итальянских, умноженное на два, плюс количество братвурстов, умноженное на три, плюс количество чоризо, умноженное на четыре, не должно превышать 10000.

Поиск оптимального решения при наличии подобных ограничений представляет собой задачу линейного программирования. Множество потенциальных решений образует выпуклый многогранник в многомерном пространстве.

В 1947 году Джордж Данциг разработал симплекс-метод, который позволял решать задачи линейного программирования довольно-таки быстро. Суть метода заключается в последовательном обходе ребер многогранника в поисках оптимальных значений.

Но если все так просто, то зачем мы тут вообще говорим о линейном программировании? На самом деле в некоторых случаях симплекс-метод не умеет выдавать быстрый результат.

В 1979 году Леонид Хачиян придумал метод эллипсоидов, в котором исходный многогранник поэтапно сжимается до тех пор, пока от него не останется одно лишь оптимальное решение. Доказав эффективность этого метода, Хачиян тем самым «переместил» задачу линейного программирования в класс P, хотя на практике метод эллипсоидов работает гораздо дольше симплекс-метода. Работа Хачияна имела огромное теоретическое значение; в последующие десятилетия на основе метода эллипсоидов было создано множество нетривиальных алгоритмов.

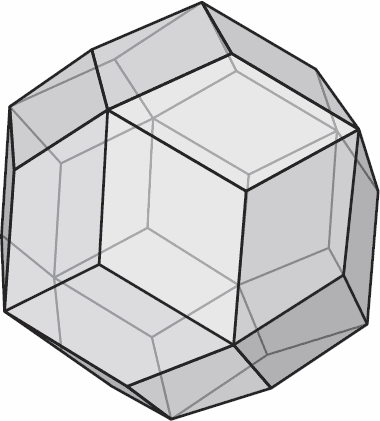
Рис. 4.12. Выпуклый многогранник

Алгоритмов стало два, причем друг на друга они абсолютно не походили; один прекрасно работал на практике, другой – в теории.

В 1984 году индийский математик Нарендра Кармаркар разработал метод внутренней точки, который тоже, как и симплекс-метод, выполняет обход многогранника, вот только «ходит» он не по внешним точкам, а по внутренним. В теории метод внутренней точки сравним по быстроте с методом эллипсоидов, а на практике он после некоторых доработок может поспорить с симплекс-методом.

Так у задачи линейного программирования появилось целых три совершенно разных по сути алгоритма. Первый – симплекс-метод – хорошо работает на практике; второй – метод эллипсоидов – в теории; третий – метод внутренней точки – хорош и там и там. Не так уж плохо для задачи, которую до самого конца семидесятых считали практически неразрешимой!

Оглавление книги