Книга: Почему

Множественные сравнения и p-значения

Множественные сравнения и p-значения

Участника исследования помещают в аппарат МРТ и показывают фотографии различных социальных ситуаций. Он должен определить эмоции, которые выражает человек на каждом кадре. С помощью МРТ ученые измеряют ток крови в локальных областях мозга и часто пользуются этим измерением как показателем мозговой активности[131], чтобы определить, какие области мозга задействованы в решении различного рода задач. Итоговые цветные изображения отражают, в каких областях наблюдается усиленный кровоток: именно это имеют в виду авторы статей, говоря, что некая область мозга «светится», реагируя на определенный стимул. Выявление активируемых областей помогает понять взаимосвязи в мозге.

Исследование обнаружило, что некоторые области мозга участника эксперимента демонстрировали статистически значимые изменения тока крови. Действительно, при том, что значение 0,05 часто используется как пороговое для p-измерений[132] (меньшие показания более значимы), уровень активности, ассоциированный с одной областью, имел p-значение 0,001[133].

Может ли эта область мозга быть связана с представлением эмоций других существ («принятие перспективы»)?

Если учесть, что объектом исследования был пойманный лосось, это кажется невероятным.

Так как же дохлая рыбина могла реагировать на визуальный стимул?

Результаты могли бы считаться высокозначимыми с учетом любых обычных пороговых значений, поэтому дело не в попытке преувеличить их важность. Чтобы понять, откуда они вообще могли взяться, сделаем небольшое отступление статистического характера.

Исследователи часто надеются определить, имеет ли некий эффект значимость (корреляция истинна, или это результат статистического отклонения), либо просто есть различие между двумя группами (активны ли разные области мозга, когда люди смотрят на людей или на животных). Но, чтобы объективно определить, какие выводы важны, необходима некая количественная мера. Одна из общепринятых мер – так называемое p-значение, которое используется для сравнения двух гипотез (нулевой и альтернативной).

P-значение показывает вероятность результата, который как минимум столь же нехарактерен, как и наблюдаемый, при условии истинности нулевой гипотезы.

Для наших целей такие гипотезы могут заключаться в следующем: между двумя вещами существует причинная зависимость (нулевая гипотеза) или нет (альтернативная гипотеза)[134].

Еще одна нулевая гипотеза: монета симметрична (альтернативная гипотеза – монета со смещением). P-значения часто интерпретируются неверно – как вероятность того, что нулевая гипотеза истинна. Хотя обычно используется пороговое значение 0,05, нет никакого закона, по которому результаты с p-значениями меньше 0,05 значимы, а больше 0,05 – нет. Это просто договоренность, и показатель 0,05 редко вызывает возражения у других ученых[135]. Условные знания не соответствуют понятиям «истинно-ложно», поскольку незначимые результаты могут иметь очень маленькие p-показатели, а значимый результат иногда не достигает критического уровня.

Фильм «Розенкранц и Гильденстерн мертвы» начинается с эпизода, в котором герои бросают найденную монетку – и оказываются в полной растерянности, когда она 157 раз падает орлом вверх[136]. Вероятность того, что монетка упадет орлом вверх 157 раз подряд, действительно крайне мала (1: 2¹⁵⁷, если быть точными), и единственный равно экстремальный результат для 157 бросков – это все решки. То, что наблюдали Розенкранц и Гильденстерн, в самом деле имело очень низкое p-значение. Но это не означает, что обязательно происходило нечто странное – только то, что подобный результат невероятен для симметричной монеты.

Для менее экстремального случая, скажем, мы подбросим монету 10 раз, и выпадут 9 орлов и 1 решка.

P-значение такого результата (здесь нулевая гипотеза – что монета симметрична, а альтернативная – что она смещена в любом направлении) – это вероятность тех самых 9 орлов и 1 решки + вероятность 9 решек и 1 орла + вероятность 10 орлов + вероятность 10 решек[137]. Причина, по которой сюда включены две серии со всеми орлами и всеми решками, в том, что мы рассчитываем вероятность события как минимум такого же экстремального, как и наблюдаемое, а эти серии – самые экстремальные. Наша альтернативная гипотеза – смещение монеты в любом направлении, а не просто в сторону орлов или решек; вот почему мы включили длинные серии решек.

На рис. 3.6 представлены гистограммы для орлов в серии из 10 бросков по 10 монет. Если бы результатом для каждой монеты было в точности 5 орлов и 5 решек, каждый график представлял бы одну черту длиной 10 пунктов с центром на отметке 5. Но в реальности случаются и большие, и меньшие значения, и даже одна серия из всех решек (показанная маленькой чертой, которая пересекает один график справа налево).

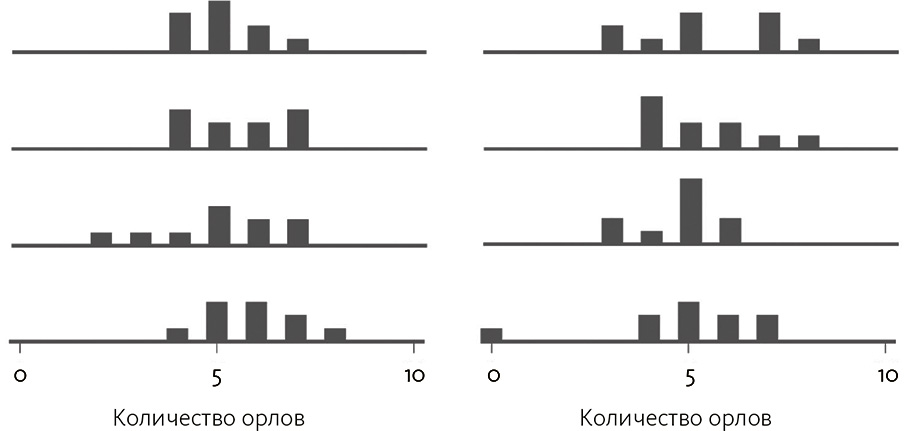
Рис. 3.6. Каждая гистограмма представляет эксперимент, где 10 монет подбрасывают 10 раз. Каждая серия из 10 монет образует точку данных на графике в зависимости от количества орлов. Показано 8 примерных экспериментов

Такое событие все равно невероятно при наличии одной симметричной монеты; но что будет, если мы подбросим 100 монет? Увеличивая число экспериментов, мы создаем больше возможностей, чтобы некое по видимости аномальное событие произошло случайно. К примеру, вероятность того, что конкретный человек выиграет в лотерею, на самом деле мала; но, если играют достаточно людей, можно гарантировать, что кто-нибудь победит. На рис. 3.7 показана такая же гистограмма, но уже для 100 монет. Действительно, будет странно, если мы не увидим как минимум одной серии из 9 или более орлов или решек, когда бросают так много монет (или лотерею, где не будет победителей, если шансы 1: 1 000 000, а играют 100 000 000 человек).

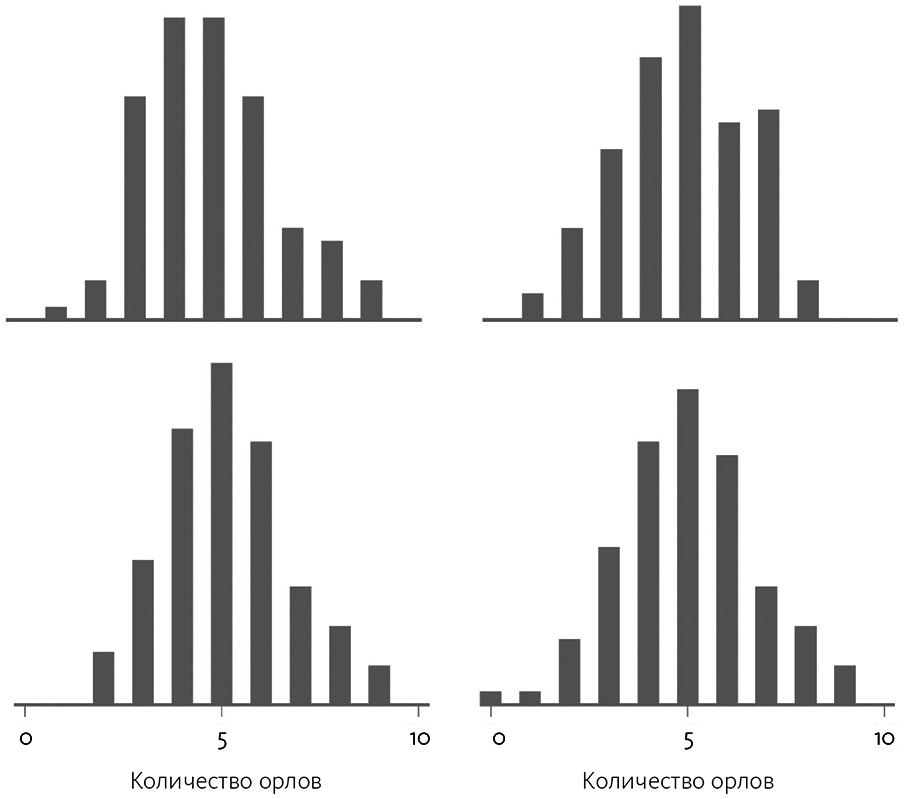
Рис. 3.7. Результаты подбрасывания 100 монет по 10 раз для каждой. Показано 4 эксперимента

Именно проблема одновременного проведения многочисленных тестов и оказалась во главе угла исследования МРТ, с рассказа о котором мы начали разговор. Проверке подверглись тысячи малых областей мозга (а в исследованиях на людях их еще больше, потому что человеческий мозг включает множество областей), поэтому совсем неудивительно, что одна из них продемонстрировала значительный кровоток. Проблемы такого вида именуются проверкой многомерной гипотезы, что означает одновременную проверку большого количества гипотез. Вопрос становится еще более существенным с появлением нового метода, генерирующего громадные наборы информации (например, множества МРТ и экспрессии генов) с так называемыми большими данными. Ранее было возможно в рамках одного эксперимента проверить только одну гипотезу, теперь же, когда мы способны анализировать тысячи переменных, неудивительно, что между ними обнаруживаются корреляции в силу количества проведенных тестов.

В эксперименте с лососем ученые протестировали тысячи гипотез, и каждая утверждала, что некая область мозга проявит значительную активность.

В действительности же исследование доказало: все эти тесты могут дать кажущиеся значимыми результаты по чистой случайности. Было показано, что при использовании статистических методов, корректных для множества сравнений (фактически каждый тест требует более жесткого порогового показателя), значимой активности выявлено не было даже при очень нежестких порогах p-значений[138].

Важная вещь, которую стоит запомнить: читая отчет о некой необходимой находке, которая была взята из громадного набора одновременных тестов, обязательно обращайте внимание на то, как авторы решают проблему множественного сравнения. Статистики расходятся во мнении, как именно (и когда) корректировать этот фактор, но все дебаты в целом сводятся к тому, какой тип ошибки хуже. Корректируя множество сравнений, мы, по сути, заявляем о желании снизить количество ложных открытий и готовы мириться с возможностью пропустить из-за этого некие значимые находки (и генерировать ложноотрицательные результаты). С другой стороны, выступая против поправок, заявляем о нежелании упускать истинно положительные результаты за счет нескольких ложных открытий.

Между этими двумя типами ошибок всегда идет поиск компромисса, а предпочтения зависят от индивидуальных целей[139]. Возможно, для эксплораторного анализа, где поиск ведется экспериментальным образом до получения конечного результата, мы считаем нужным, образно говоря, раскинуть обширную сеть. С другой стороны, если мы стараемся отобрать узкоцелевую группу кандидатов для разработки дорогостоящего препарата, каждое ложное умозаключение способно привести к массе впустую потраченного времени и средств.

Оглавление книги