Книга: Почему

Что такое корреляция

Что такое корреляция

Х ассоциируется с раком, Y связан с припадками, а Z привязан к сердечным приступам. Каждый термин описывает корреляцию, сообщая, что эти явления соотносятся между собой. Хотя и не говоря, как именно.

Суть в том, что две переменные коррелируют, если изменения в одной из них ассоциируются с изменениями в другой. К примеру, рост и возраст детей коррелируют, потому что увеличение возраста соответствует увеличению роста: дети, как правило, с годами растут. Эти соотношения могут быть выборочными (измерения множества детей различного возраста за один раз), временными (измерения одного ребенка в течение жизни) или учитывать оба фактора (измерения разных людей в течение долгого срока). С другой стороны, между ростом и месяцем рождения нет долговременной корреляции. Это значит, что если месяц рождения варьируется, то рост так регулярно не меняется.

На рис. 3.1 (a) продемонстрировано, как возрастные изменения соотносятся с изменениями роста. Если увеличивается одна переменная, вместе с ней растет и другая. Напротив, на рис. 3.1 (б), где показаны рост и месяц рождения, мы видим набор случайно размещенных точек: месяц рождения варьируется, но соответствующего изменения в росте нет.

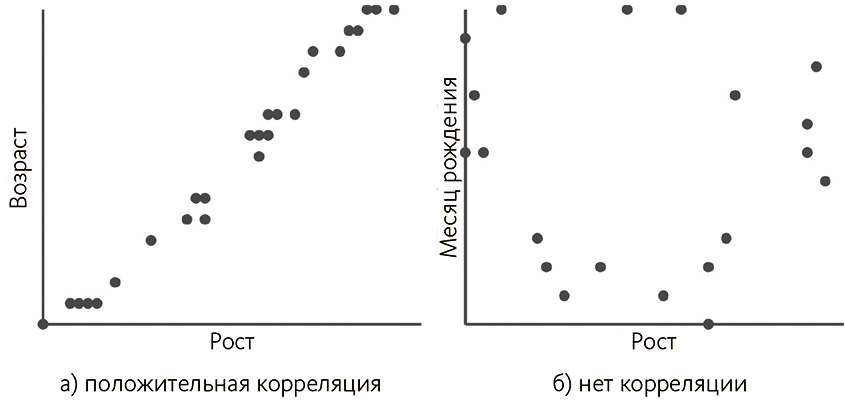
Рис. 3.1. Возраст и рост коррелируют, но рост и месяц рождения – нет

Это также означает, что, зная возраст ребенка, мы можем примерно предсказать его рост, а зная месяц рождения – нет. Чем ближе точки друг к другу, формируя линию, тем точнее наши прогнозы (поскольку при этом взаимосвязи теснее). Предсказание – одна из ключевых сфер применения корреляций, и в ряде случаев его можно сделать и без причинных взаимосвязей (хотя не всегда успешно).

Когда корреляции сильны, они могут приобретать видимые очертания, как на рис. 3.1 (a). Но нам необходимы методы измерения этой силы, чтобы провести количественное сравнение и оценку. Существует много единиц измерения корреляций, а одна из них наиболее употребительна – коэффициент корреляции Пирсона (обычно его обозначают буквой r)[113]. Этот показатель может иметь значение от 1 до –1. При значении 1 переменные обладают абсолютной положительной корреляцией (положительное изменение одной переменной прямо соответствует положительному изменению другой), а значение – 1 говорит об их абсолютной отрицательной корреляции (если одна переменная уменьшается, другая всегда увеличивается).

Получается, коэффициент корреляции Пирсона показывает, как варьируются вместе две переменные по сравнению с индивидуальными модуляциями (эти две меры называются «ковариация» и «вариация»). К примеру, мы можем отметить, сколько часов студенты в некой группе проводят за подготовкой к заключительному экзамену, чтобы посмотреть на соотношение показателей. Зная о наборе экзаменационных баллов и количестве часов, проведенных за подготовкой, но не имея возможности сопоставить итоговые оценки и соответствующие временные показатели, мы не определим, есть ли между ними корреляция. В этом случае получится наблюдать индивидуальные вариации каждой переменной, но не их взаимоизменения. То есть мы не можем выяснить, действительно ли большее время, потраченное на занятия, сопровождается более высокими оценками.

Скажем, вы хотите узнать, как получить грант, поэтому спрашиваете всех друзей, которые его имеют, что, по их мнению, помогло им. Все кандидаты оформляли заявку шрифтом Times New Roman; согласно мнению половины, важно, чтобы на каждой странице была как минимум одна иллюстрация; а треть рекомендуют представить заявку за 24 часа до установленного срока.

Означает ли это, что есть корреляция между названными условиями и получением гранта? Нет, не означает, потому что, не видя вариации исходного результата, нельзя определить, соотносится ли с ним какой-то иной фактор.

К примеру, если в течение некоей последовательности дней, когда температура доходила до 80°F (примерно 26,6 °C), на углу улицы стояли две тележки с мороженым, трудно сказать о корреляции погоды и мороженщиков, поскольку нет вариации значения той или другой переменной (температуры или количества мороженщиков). То же справедливо и для случая, когда есть вариация только одной переменной – например, на улице всегда два мороженщика, а температура изменяется от 80 до 90 градусов. Этот сценарий показан на рис. 3.2: отсутствие вариации ведет к тому, что данные скопились в одной точке, а модуляция единственной переменной дает горизонтальную линию[114]. Именно такой вариант в примере с грантом. Поскольку все результаты идентичны, нельзя сказать, что произойдет, если поменять шрифт или представить заявку за минуту до истечения срока.

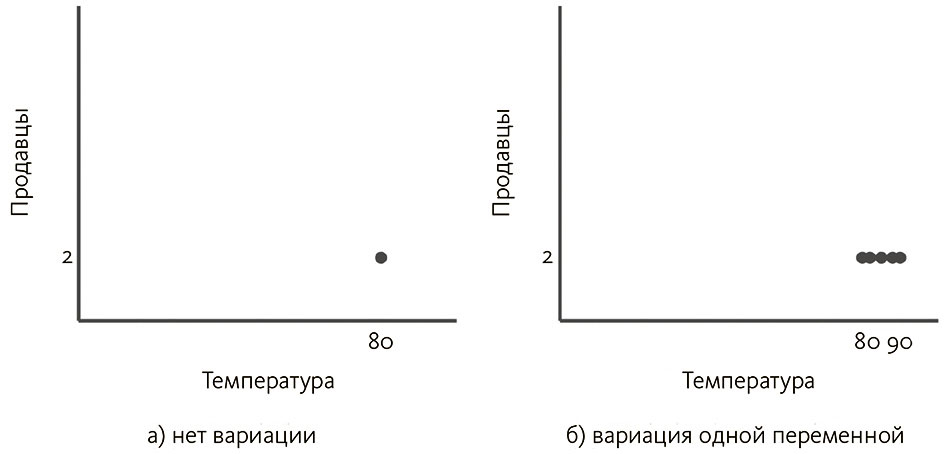
Рис. 3.2. Не наблюдая вариации обеих переменных, нельзя обнаружить корреляцию

И тем не менее широко распространена ситуация, когда анализируются только факторы, ведущие к определенному исходу. Только представьте, насколько часто победителей спрашивают, как именно они добились успеха, а потом стараются этот успех воспроизвести, выполняя в точности те же действия. Подобный подход полон недостатков по многим причинам, включая то, что люди просто не слишком хорошо умеют определять существенные факторы, недооценивают роль случайностей и переоценивают свои способности[115]. В результате мы не только путаем факторы, которые по чистой случайности сопутствуют желаемому эффекту, с теми, которые действительно его обеспечивают, но и видим иллюзорные корреляции там, где их нет.

К примеру, многие интересуются, действительно ли музыкальное образование соотносится с профессиональными успехами в других областях. Даже если мы обнаружим, что многие успешные люди (как бы мы ни определяли успех) играют на музыкальных инструментах, эти ничего не скажет о существовании корреляции – не говоря уже о причинно-следственной связи. Если напрямую спросить, верят ли они, что музыка помогает развивать и другие способности, многие, безусловно, отметят некую взаимосвязь. Но с гораздо меньшей вероятностью они сделают это, если интересоваться конкретно умением играть в шахматы, быстро бегать или тем, сколько кофе вы выпиваете каждый день.

Для целей этой книги важнее всего следующее: беседы с победителями бесполезны, поскольку можно сделать то же самое, но не преуспеть. Возможно, все кандидаты оформляют заявки на грант шрифтом Times New Roman (а значит, те, кто не получил гранты, порекомендуют использовать другой шрифт), а может, успешные кандидаты получили грант, несмотря на избыточное количество иллюстраций в документах. Не зная совокупности положительных и отрицательных примеров, мы не сможем даже предположить наличие корреляции.

Скажем, мы исследуем студенческий пул, чтобы выяснить, сколько чашек кофе молодые люди выпивают перед финальным экзаменом, а потом регистрируем полученные баллы. Гипотетические данные этого примера представлены на рис. 3.3 (а). Корреляция очень сильна и равна почти 1 (0,963, если быть точными), поэтому точки на графике тесно окружают некую невидимую линию. Если взять обратное отношение (0 чашек кофе соответствуют 92 экзаменационным баллам, а 10 чашек – 10 баллам), чтобы сформировать отрицательную ассоциацию, абсолютное значение окажется тем же, а единственное, что изменится, – знак коэффициента корреляции. Тогда показатель измерения будет равен почти –1 (–0,963), а кривая станет отраженным по горизонтали вариантом положительно коррелирующих данных, как показано на рис. 3.3 (б).

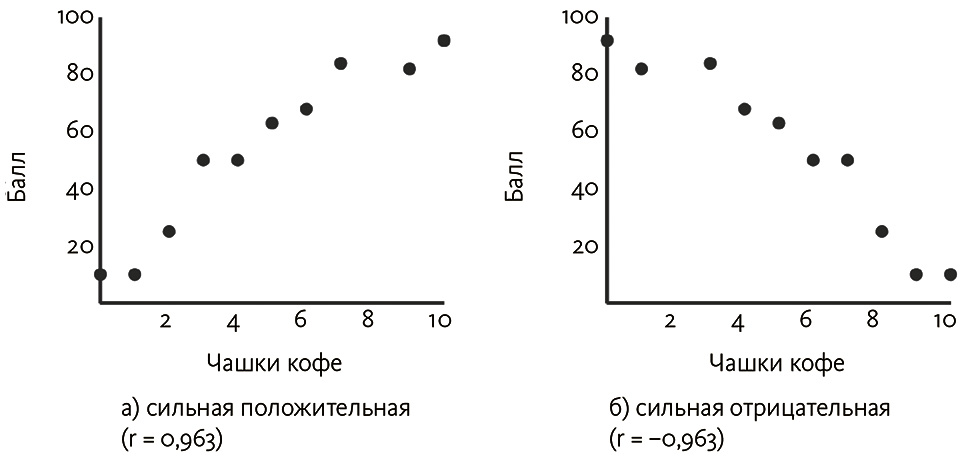
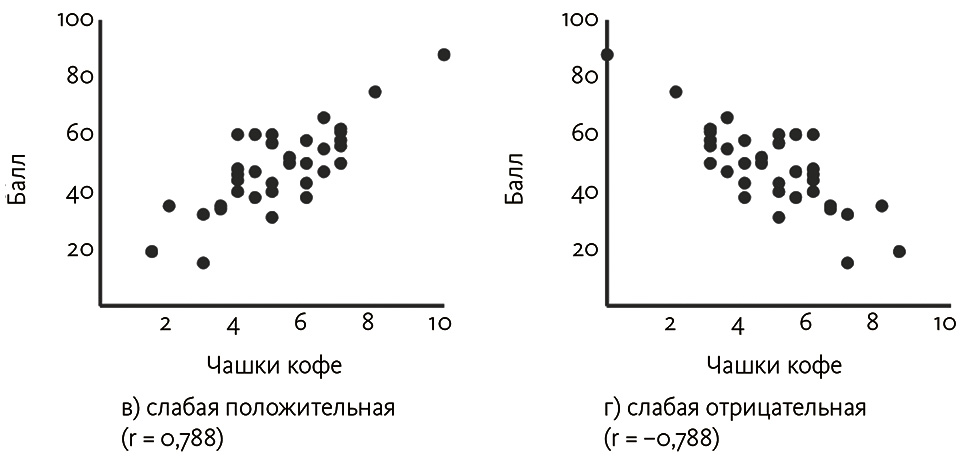
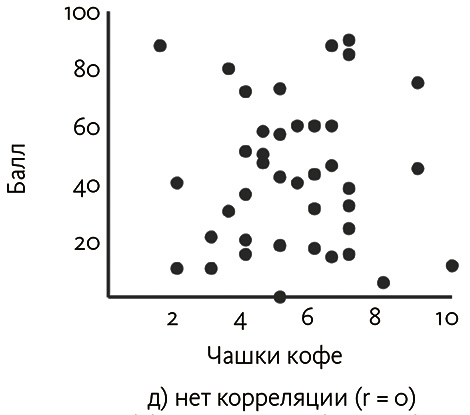
Рис. 3.3. Корреляции между потреблением кофе и экзаменационными баллами

С другой стороны, если бы каждое из этих отношений стало слабее и имела место повышенная вариация результатов экзамена для каждого уровня потребления кофе, наблюдалась бы дисперсия точек, и корреляция была бы слабее. Это продемонстрировано на рис. 3.3 (в), где точки на графике по-прежнему имеют в основном линейную форму, но отклоняются от центра гораздо дальше.

Как и ранее, инверсия отношения (потребление кофе коррелирует с худшими оценками) формирует кривую на рис. 3.3 (г), где единственным отличием оказывается нисходящий уклон.

Заметим, что, если отношение слабое, гораздо труднее перейти от значения потребления кофе до экзаменационных баллов и обратно. Это четко видно, если в первых примерах выбор значения одной из переменных сильно ограничивает вероятные значения другой. Но если мы попытаемся предсказать экзаменационные баллы для 4 чашек кофе с более слабой корреляцией, прогноз будет гораздо менее точен, поскольку мы наблюдали более широкий диапазон баллов для такого уровня потребления кофе. Предел для этой возрастающей вариации – пара переменных, которые абсолютно не соотносятся (имеют нулевой коэффициент корреляции), как показано на рис. 3.3 (д), при этом нельзя вообще ничего сказать о результатах экзаменов на основе выпитого кофе.

Или мы захотели узнать, насколько сильна корреляция между тем, где человек живет, и его умением водить машину. Мера, о которой мы говорили до сих пор, применяется для неквантованных[116] данных, таких как цены на акции, а не дискретных, таких как местонахождение или киножанр. Если у нас всего две переменные, каждая из которых принимает только два значения, лучше взять упрощенный вариант коэффициента корреляции Пирсона – так называемый фи-коэффициент[117].

Например, можно проверить соотношение между местом, где люди живут, и их умением водить машину. Местом жительства может быть либо город, либо пригород / сельская местность, а факт вождения может либо иметь место (да), либо нет. Как и ранее, проверяем, как эти условия варьируются. Здесь вариация означает частоту, с которой они наблюдаются совместно (а не то, как значения увеличиваются или уменьшаются).

В табл. 3.1 показано, какой вид могут принимать данные. Фи-коэффициент для них составляет 0,81. Мы изначально смотрим, сосредоточено ли большинство измерений вдоль диагональной линии на таблице. Если значения в основном находятся в группах вождение/не-город и не-вождение/город, можно говорить о положительной корреляции.

Если аккумулируются вдоль другой диагонали, корреляция имеет такую же силу, но другой знак.

Таблица 3.1. Различные комбинации местонахождения и вождения

Однако на основе этих измерений не каждая сильная корреляция будет иметь высокое значение. Применение коэффициента Пирсона предполагает, что это отношение линейно, а значит, если одна переменная (например, рост), увеличивается, другая (например, возраст) также увеличивается, причем с одинаковым темпом. Это не всегда справедливо, поскольку могут встречаться и более сложные, нелинейные отношения. К примеру, если из-за нехватки кофе человек становится вялым (и не способен показать хорошие результаты на экзамене), а избыток кофе его возбуждает (и тоже плохо влияет на результаты), то график, выстроенный на основе некоторых данных, может иметь вид, как на рис. 3.4. Здесь видно повышение балла в диапазоне от 0 до 5 чашек кофе, потом еще одно медленное падение. Хотя корреляция Пирсона для этого примера нулевая, данные показывают четкий паттерн.

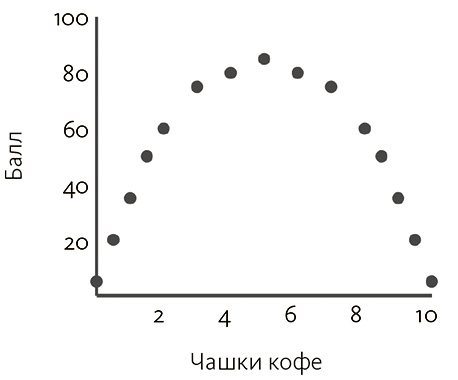
Рис. 3.4. Нелинейное отношение (r = 0,000)

Подобный тип отношений показывает неоднозначные результаты при многих методах причинных умозаключений. В последующих главах мы вернемся к этому. Его важно иметь в виду, поскольку он встречается в таких прикладных науках, как биомедицина (например, и недостаток, и передозировка витаминов могут иметь последствия для здоровья) и финансы (например, кривая Лаффера, которая показывает зависимость между доходами государства и динамикой налоговых ставок).

Аналогично, если вес детей всегда увеличивается с возрастом, но экспоненциально (дети растут, и их вес растет все сильнее), корреляция Пирсона будет ниже ожидаемой, так как она работает в линейных зависимостях. Это одна из опасностей, подстерегающая тех, кто бросает данные в «черный ящик» и просто принимает любые полученные результаты, не проводя дальнейших исследований. Поступив так, когда корреляция недооценивается или даже кажется равной нулю, мы упускаем потенциально интересные зависимости.

Это одна из причин, почему нельзя интерпретировать нулевую корреляцию (пирсоновскую или любую другую) как вообще незначимую (существуют и другие причины, например ошибки в измерениях или первичные данные, искажающие результаты). Еще одна важная причина заключается в том, что данные могут не быть репрезентативными с точки зрения исходного распределения. Если бы нам разрешили взглянуть на статистику смертей от гриппа, но предоставили только данные о количестве больных, поступивших в лечебные учреждения, и вызовов скорой помощи, мы наблюдали бы гораздо более высокий процент летальных исходов, чем в масштабах всего населения. Это происходит потому, что люди оказываются в стационаре, как правило, с более тяжелыми случаями или дополнительными заболеваниями (и с высокими шансами смерти от гриппа). Итак, мы снова сравниваем не все исходы, а только статистику для больных или обратившихся к врачам на фоне симптоматики гриппа.

Чтобы проиллюстрировать эту проблему в ограниченном диапазоне, возьмем, к примеру, две переменные: общий экзаменационный балл и часы, потраченные на подготовку. Однако вместо данных по всему спектру оценок за экзамен мы имеем только сведения о лицах, получивших общий балл за письменный и устный тест по математике выше 1400. На рис. 3.5 эта область показана серым цветом.

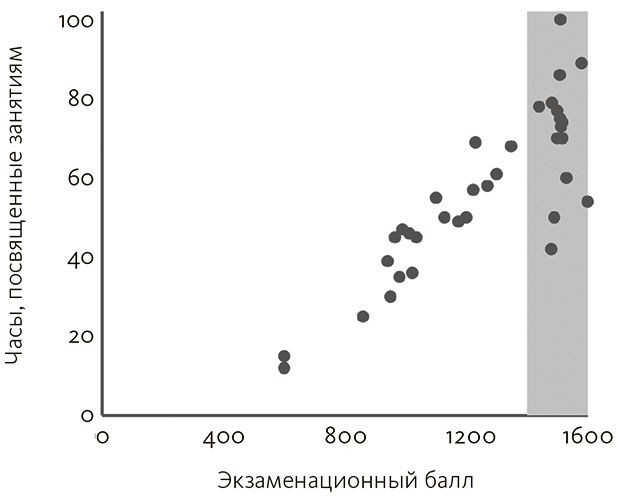
Рис. 3.5. Закрашенная область представляет ограниченный диапазон данных

Согласно этим гипотетическим показателям, студенты с высокими баллами представляют собой комбинацию как лиц с природной одаренностью (которые преуспевают, особо не утруждаясь), так и тех, кто получил лучшие оценки за счет интенсивных занятий. Если воспользоваться только данными из закрашенной области, мы не обнаружим никакой корреляции между переменными; но если применить информацию по всему спектру экзаменационных показателей, созависимость будет сильной (корреляция Пирсона оценки и упорных занятий для закрашенной области равна 0, а для всего набора данных – 0,85).

Оборотная сторона медали – это корреляции, которые мы порой находим между несвязанными переменными, опираясь только на следствия (то есть принимая во внимание только случаи, когда это следствие имеет место). К примеру, получение высокого экзаменационного балла и участие во множестве факультативных мероприятий обеспечивают прием в престижный университет. Значит, данные, взятые только в вузах, покажут корреляцию между высоким баллом и многочисленными факультативами, так как здесь эти показатели чаще всего в наличии.

Подобная тенденция отбора данных довольно типична. Возьмем, к примеру, сайты, опрашивающие посетителей насчет их политических взглядов. В интернете не получится отобрать участников опроса случайно в масштабах всего населения, а данные источников с сильным политическим уклоном искажены еще сильнее. Если посетители конкретной страницы активно поддерживают действующего президента, то результаты по ним, возможно, покажут, что рейтинг главы государства растет каждый раз, когда он произносит важную речь. Однако это показывает лишь то, что есть корреляция одобрения президента и произнесения им речей перед сторонниками (поскольку на вопросы отвечают представители всего населения). Мы рассмотрим и эту, и другие формы трендов (например, смещение по выживаемости) в главе 7 и увидим, как они влияют на результаты анализа экспериментальных данных.

Важно помнить, что, помимо математических причин, по которым можно распознать ложные корреляции, есть еще наблюдение за данными, позволяющее найти ложные паттерны. Некоторые из когнитивных смещений, заставляющие нас видеть соотношение несвязанных факторов, также сходны с ошибкой отбора. К примеру, предвзятость подтверждения заставляет искать доказательства в пользу определенного убеждения. Иными словами, если вы верите, что лекарство вызывает некий побочный эффект, вы приметесь читать в интернете отзывы тех, кто уже принимал его и наблюдал это действие. Но таким образом вы игнорируете весь набор данных, не поддерживающих вашу гипотезу, вместо того чтобы искать свидетельства, которые, возможно, заставят ее переоценить. Предвзятость подтверждения также может заставить вас отказаться от свидетельств, противоречащих вашей гипотезе; вы можете предположить, что источник сведений ненадежен или что исследование основывалось на ошибочных экспериментальных методах.

Помимо предвзятости с точки зрения доказательств, может случиться ошибка интерпретации аргументов. Если в ходе «неслепого» тестирования нового лекарства доктор помнит, что пациент принимает это средство и считает, что оно ему помогает, то может начать искать признаки его эффективности. Поскольку многие параметры субъективны (например, подвижность или усталость), это может привести к отклонениям в оценке данных индикаторов и логическим заключениям о наличии несуществующих кореляций[118]. Этот пример взят из реального исследования, где доктора, выведенные из слепого метода, сделали вывод об эффективности препарата (мы подробнее обсудим ситуацию в главе 7). Таким образом, интерпретация данных может различаться в зависимости от убеждений, что приводит к отличиям в результатах[119].

Есть и специфическая форма предвзятости подтверждения – иллюзорная корреляция. Она означает поиск соотношения там, где его нет. Возможная взаимосвязь симптомов артрита и погоды настолько широко разрекламирована, что считается доказанной. Однако знание о ней может привести к тому, что пациенты будут говорить о корреляции просто из ожидания ее увидеть. Когда ученые попытались проанализировать эту проблему, взяв за основу обращения пациентов, клинические анализы и объективные показатели, то не обнаружили абсолютно никакой связи (а другие выяснили, что истинным виновником могла быть сырость, хотя и этот вывод не окончателен)[120]. А когда студентам колледжей показали данные из анкет пациентов, где отмечались одновременно болевые симптомы и атмосферное давление, те не только увидели корреляции там, где их не было, но и представили разные интерпретации одних и тех же последовательностей как положительно или отрицательно соотносящихся.

Это подобно ошибке отбора, поскольку одной из причин выявления неверной корреляции может быть концентрация на одном сегменте информации. Если вы прогнозируете отрицательное соотношение переменных, легко сосредоточите внимание на небольших сегментах целого, подтверждающих ваш прогноз. И такой случай относится к предвзятости подтверждения: можно сфокусировать внимание на определенных данных, повинуясь сформированным убеждениям. В случае с артритом и погодой люди, возможно, придают слишком большое значение определенным фактам (отбрасывая проявившиеся симптомы при хорошей погоде и придавая особое значение таким же при плохой) или видят доказательства там, где их нет (по-разному отмечают заболевание в зависимости от погоды и от ожидаемой связи того и другого).

Оглавление книги