Книга: Programming with POSIX® Threads
1.6.1 Parallelism
1.6.1 Parallelism
On a multiprocessor system, threading allows a process to perform more than one independent computation at the same time. A computation-intensive threaded application running on two processors may achieve nearly twice the performance of a traditional single-threaded version. "Nearly twice" takes into account the fact that you'll always have some overhead due to creating the extra thread(s) and performing synchronization. This effect is often referred to as "scaling." A two-processor system may perform 1.95 times as fast as a single processor, a three-processor system 2.9 times as fast, a four-processor system 3.8 times as fast, and so forth. Scaling almost always falls off as the number of processors increases because there's more chance of lock and memory collisions, which cost time.
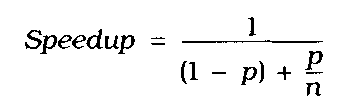
FIGURE 1.1 Amdahl's law
Scaling can be predicted by "Amdahl's law," which is shown in Figure 1.1. In the equation, p represents the ratio of "parallelizable code" over "total execution time," and n represents the number of processors the code can use. The total elapsed time for a parallel job is the sum of the elapsed time for the nonparallelizable work (1 - p) and the elapsed time for each processor executing the parallelizable work (p/n).
Amdahl's law is a simple relationship showing how parallelism is limited by the amount of serialization needed. When the program has no parallelizable code (p is 0), the speedup is 1. That is, it is not a parallel program. If the program requires no synchronization or other serial code (p is 1), then the speedup is n (the number of processors). As more synchronization is required, parallelism provides less benefit. To put it another way, you'll get better scaling with activities that are completely independent than with activities that are highly dependent: The independent activities need less synchronization.
The diagram in Figure 1.2 shows the effect of Amdahl's law. "Clock time" progresses from left to right across the page, and the diagram shows the number of processors working in parallel at any moment. Areas where the diagram has only a single horizontal line show that the process is serialized. Areas that have several horizontal lines in parallel show where the process benefits from multiple processors. If you can apply multiple processors for only 10% of your program's execution time, and you have four processors, then Amdahl's law predicts a speedup of 1 / (0.9+( 0.1 /4)), or about 8%.
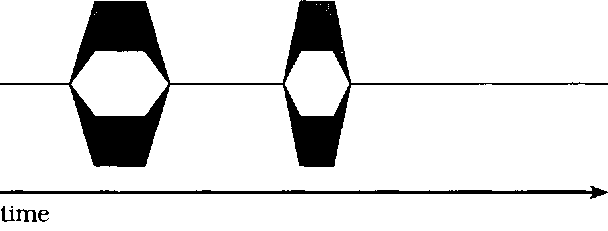
FIGURE 1.2 Parallelism charted against time
Operations on large matrices can often be "parallelized" by splitting the matrix into pieces. For example, each thread may be able to operate on a set of rows or columns without requiring any data written by threads operating on other slices. You still generally need to synchronize threads at the beginning and end of processing the matrix, frequently using a barrier[1]. Amdahl's law shows that you'll get better performance by giving each thread a large and relatively independent "chunk" of work, requiring infrequent synchronization, than by giving them smaller chunks.
Amdahl's law is an excellent thought exercise to help you understand scaling. It is not, however, a practical tool, because it is nearly impossible to accurately compute p for any program. To be accurate, you need to consider not only all serialized regions within your code, but also within the operating system kernel and even in hardware. Multiprocessor hardware must have some mechanism to synchronize access to the contents of memory. When each processor has a private data cache, the contents of those caches must be kept consistent with each other and with the data in memory. All of this serialization must be included in any accurate calculation.




